Under the Hood: Training a Digit Classifier
确切地说,我们将讨论 array 和 tensor 以及广播机制,这是一种表达使用它们的强大技术。我们将解释随机梯度下降(SGD),这是通过自动更新权重来学习的机制。我们将讨论我们基本分类任务的损失函数的选择,以及小批量处理的作用。我们还将描述一个基本神经网络实际正在做的数学。最后,我们将把所有这些碎片放在一起。
在未来章节中,我们还将深入探讨其他应用程序,并了解这些概念和工具是如何概括的。但这一章是关于奠基的。坦率地说,这也使这一章成为最困难的章节之一,因为这些概念都是相互依赖的。像拱门一样,所有的石头都需要到位,才能让结构保持向上。同样像拱门一样,一旦发生这种情况,它就是一个强大的结构,可以支持其他事情。但组装起来需要一些耐心。
我们开始吧。第一步是考虑图像如何在计算机中表示。
Pixels: The Foundations of Computer Vision
为了了解计算机视觉模型中发生的事情,我们首先必须了解计算机如何处理图像。我们将使用计算机视觉中最著名的数据集之一MNIST进行实验。MNIST包含由国家标准和技术研究所收集并由Yann Lecun及其同事整理成机器学习数据集的手写数字图像。Lecun于1998年在Lenet-5中使用了MNIST,这是第一个演示手写数字序列实用识别的计算机系统。这是人工智能史上最重要的突破之一。
Sidebar: Tenacity and Deep Learning
深度学习的故事是少数敬业研究人员坚韧不拔的故事之一。在早期的希望(和炒作!)之后神经网络在20世纪90年代和21世纪初失宠,只有少数研究人员一直在努力使它们正常工作。其中三人,Yann Lecun、Yoshua Bengio和Geoffrey Hinton,在经历了更广泛的机器学习和统计界的深刻怀疑和不感兴趣后,于2018年获得了计算机科学的最高荣誉图灵奖(通常被称为“诺贝尔计算机科学奖”)。
杰夫·辛顿(Geoff Hinton)说,即使学术论文的结果比以前发表的任何论文都好得多,也会仅仅因为使用神经网络而被顶级期刊和会议拒绝。Yann Lecun关于卷积神经网络的工作(我们将在下一节中进行研究)表明,这些模型可以阅读手写文本——这是以前从未实现过的。然而,他的突破被大多数研究人员忽视了,即使它被商业化地用于阅读美国10%的支票!
除了这三位图灵奖得主外,还有许多其他研究人员一直在努力让我们走到今天的位置。例如,Jurgen Schmidhuber(许多人认为他应该分享图灵奖)开创了许多重要想法,包括与学生Sep Hochreiter合作研究长短期记忆(LSTM)架构(广泛用于语音识别和其他文本建模任务,并在<>中的IMDb示例中使用)。也许最重要的是,Paul Werbos在1974年发明了神经网络的反向传播,这是本章所示的技术,并普遍用于训练神经网络(Werbos,1994年)。几十年来,他的发展几乎被完全忽视了,但今天,它被认为是现代人工智能最重要的基础。
这里有给我们所有人的教训!在您的深度学习旅程中,您将面临许多障碍,包括技术障碍,以及(甚至更困难的)您周围不相信您会成功的人造成的障碍。有一种有保证的失败方式,那就是停止尝试。我们看到,在每一个FastAI学生中,唯一一贯的特征是,他们都是非常顽强的。
End sidebar
在本初始教程中,我们将尝试创建一个模型,该模型可以将任何图像归类为3或7。因此,让我们下载一个包含以下数字图像的MNIST示例:
1
path = untar_data(URLs.MNIST_SAMPLE)
1
2
#hide
Path.BASE_PATH = path
我们可以使用 fastai 添加的方法 ls 查看此目录中的内容。此方法返回一个名为 L 的特殊fastai类的对象,该类具有Python内置 list 的所有相同函数,以及更多函数。它的一个方便的函数是,在打印时,它会在列出项目本身之前显示项目数量(如果有超过10个项目,它只显示前几个项目):
1
2
3
path.ls()
(#9) [Path('cleaned.csv'),Path('item_list.txt'),Path('trained_model.pkl'),Path('models'),Path('valid'),Path('labels.csv'),Path('export.pkl'),Path('history.csv'),Path('train')]
MNIST数据集遵循机器学习数据集的通用布局:训练集和验证集(和/或测试集)的单独文件夹。让我们看看训练集里有什么:
1
2
3
(path/'train').ls()
(#2) [Path('train/7'),Path('train/3')]
有一个 3 文件夹和一个 7 文件夹。在机器学习术语中,我们说“3”和“7”是此数据集中的标签(或目标)。让我们看看其中一个文件夹(使用排序来确保我们都能获得相同的文件顺序):
1
2
3
4
5
threes = (path/'train'/'3').ls().sorted()
sevens = (path/'train'/'7').ls().sorted()
threes
(#6131) [Path('train/3/10.png'),Path('train/3/10000.png'),Path('train/3/10011.png'),Path('train/3/10031.png'),Path('train/3/10034.png'),Path('train/3/10042.png'),Path('train/3/10052.png'),Path('train/3/1007.png'),Path('train/3/10074.png'),Path('train/3/10091.png')...]
正如我们可能预期的那样,它充满了图像文件。我们现在来看看一个。这是一张手写数字3的图像,取自著名的MNIST手写数字数据集:
1
2
3
im3_path = threes[1]
im3 = Image.open(im3_path)
im3

在这里,我们使用Python成像库(PIL)中的 Image类,这是用于打开、操作和查看图像的最广泛使用的Python软件包。Jupyter了解PIL图像,因此它会自动为我们显示图像。
在计算机中,一切都以数字表示。要查看构成此图像的数字,我们必须将其转换为NumPy数组或PyTorch张量。例如,以下是图像的一部分,转换为NumPy数组:
1
2
3
4
5
6
7
8
9
array(im3)[4:10,4:10]
array([[ 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, 0, 0, 29],
[ 0, 0, 0, 48, 166, 224],
[ 0, 93, 244, 249, 253, 187],
[ 0, 107, 253, 253, 230, 48],
[ 0, 3, 20, 20, 15, 0]], dtype=uint8)
4:10 表示我们请求从索引4(包含)到10(不包括)的行,以及列的行数相同。NumPy索引从上到下以及从左到右,因此此部分位于图像的左上角。以下是与PyTorch张量相同的内容:
1
2
3
4
5
6
7
8
tensor(im3)[4:10,4:10]
tensor([[ 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, 0, 0, 29],
[ 0, 0, 0, 48, 166, 224],
[ 0, 93, 244, 249, 253, 187],
[ 0, 107, 253, 253, 230, 48],
[ 0, 3, 20, 20, 15, 0]], dtype=torch.uint8)
我们可以切片数组,只选择顶部有数字的部分,然后使用 Pandas DataFrame 使用渐变对值进行颜色编码,这清楚地向我们展示了图像是如何从像素值创建的:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#hide_output
im3_t = tensor(im3)
df = pd.DataFrame(im3_t[4:15,4:22])
df.style.set_properties(**{'font-size':'6pt'}).background_gradient('Greys')
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 29 150 195 254 255 254 176 193 150 96 0 0 0
2 0 0 0 48 166 224 253 253 234 196 253 253 253 253 233 0 0 0
3 0 93 244 249 253 187 46 10 8 4 10 194 253 253 233 0 0 0
4 0 107 253 253 230 48 0 0 0 0 0 192 253 253 156 0 0 0
5 0 3 20 20 15 0 0 0 0 0 43 224 253 245 74 0 0 0
6 0 0 0 0 0 0 0 0 0 0 249 253 245 126 0 0 0 0
7 0 0 0 0 0 0 0 14 101 223 253 248 124 0 0 0 0 0
8 0 0 0 0 0 11 166 239 253 253 253 187 30 0 0 0 0 0
9 0 0 0 0 0 16 248 250 253 253 253 253 232 213 111 2 0 0
10 0 0 0 0 0 0 0 43 98 98 208 253 253 253 253 187 22 0
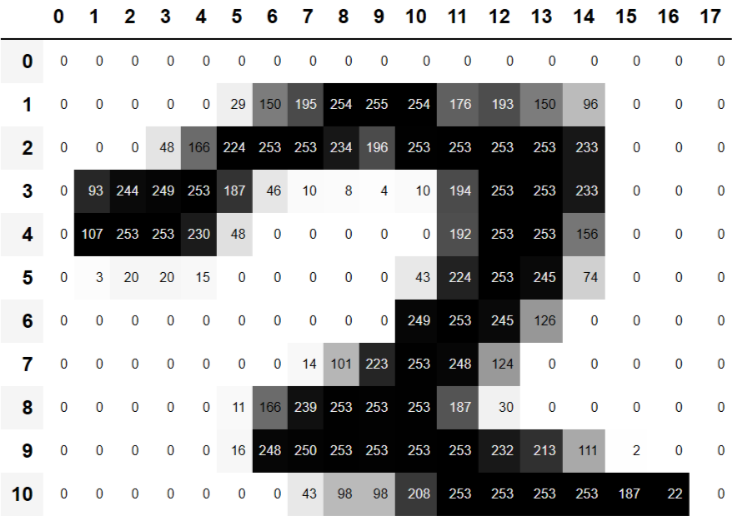
你可以看到背景白色像素存储为数字0,黑色是数字255,灰色阴影在两者之间。整个图像包含28个像素宽,28个像素向下,共784个像素。(这比您从手机摄像头中获得的图像要小得多,手机摄像头有数百万像素,但对我们的初步学习和实验来说是一个方便的尺寸。我们很快就会构建更大的全彩图像。)
因此,现在您已经看到了计算机图像的样子,让我们回顾一下我们的目标:创建一个可以识别 3 和 7 的模型。你怎么去找一台电脑来做那件事?
First Try: Pixel Similarity
所以,这是第一个想法:我们找到 3 中每个像素的平均像素值,然后对 7 也这样做。这将给我们两个小组平均值,定义我们所谓的“理想”3和7。然后,要将图像分类为一位或另一位数字,我们可以看到图像与这两个理想数字中最相似的哪个。这看起来肯定应该比什么都没有好,所以它会成为一个好的基线。
行话:基线:一个你确信的简单模型应该表现得相当好。它的实施应该非常简单,测试也非常容易,这样您就可以测试每个改进的想法,并确保它们总是比您的基线更好。如果不从合理的基线开始,就很难知道你的超级花哨的模型是否真的有什么好处。创建基线的一个好方法是做我们在这里做的事情:想出一个简单、易于实施的模型。另一个好方法是四处搜索,找到其他解决与您类似的问题的人,并在您的数据集中下载和运行他们的代码。理想情况下,试试这两个!
我们简单模型的第一步是获得我们两组中每个组像素值的平均值。在这个过程中,我们将学习许多整洁的Python数值编程技巧!
让我们创建一个张量,其中包含我们堆叠在一起的所有 3。我们已经知道如何创建包含单个图像的张量。要创建包含目录中所有图像的张量,我们将首先使用Python列表理解来创建单个图像张量的纯列表。
我们将使用Jupyter对一路上的工作进行一些小检查——在这种情况下,确保返回数量似乎合理:
1
2
3
4
5
seven_tensors = [tensor(Image.open(o)) for o in sevens]
three_tensors = [tensor(Image.open(o)) for o in threes]
len(three_tensors),len(seven_tensors)
(6131, 6265)
注意:列表理解:列表和字典理解是Python的一个精彩功能。许多Python程序员每天都使用它们,包括这本书的作者——它们是“idiomatic Python”的一部分。但来自其他语言的程序员可能以前从未见过他们。只需在网上搜索一下,就有很多很棒的教程,所以我们现在不会花很长时间讨论它们了。这里有一个快速的解释和示例,让你开始。列表理解如下:new_list = [f(o) for o in a_list if o>0]。这将在将a_list传递给函数f后返回大于0的每个元素。这里有三个部分:您正在迭代的集合(a_list)、可选过滤器(如果o>0),以及对每个元素(f(o))要做的事情。它不仅写得更短,而且比使用循环创建同一列表的替代方法快得多。
我们还将检查其中一张图像是否看起来不错。由于我们现在有张量(默认情况下,Jupyter将打印为值),而不是PIL图像(默认情况下Jupyter将显示为图像),我们需要使用fastai的 show_image 函数来显示它:
1
show_image(three_tensors[1]);
对于每个像素位置,我们希望计算该像素强度的所有图像的平均值。为此,我们首先将列表中的所有图像组合成一个三维张量。描述这种张量的最常见方法是将其称为 秩-3张量。我们通常需要在集合中将单个张量堆叠成单个张量。PyTorch附带了一个名为 stack 的函数,我们可以用于此目的。
PyTorch中的一些操作,例如取平均值,要求我们将整数类型转换为浮点类型。由于我们稍后需要这个,我们现在还将张量 cast 为浮点型。在PyTorch中 cast 就像键入您想要 cast 的类型名称一样简单。
一般来说,当图像是浮点数时,像素值预计在0到1之间,因此我们还将在这里除以255:
1
2
3
4
5
stacked_sevens = torch.stack(seven_tensors).float()/255
stacked_threes = torch.stack(three_tensors).float()/255
stacked_threes.shape
torch.Size([6131, 28, 28])
也许张量最重要的属性是它的形状。这告诉你每个轴的长度。在这种情况下,我们可以看到我们有6131张图像,每张尺寸为28×28像素。这个张量没有具体说明第一轴是图像的数量,第二轴是高度,第三轴是宽度——张量的语义完全取决于我们,以及我们如何构造它。就PyTorch而言,这只是记忆中的一堆数字。
张量形状的长度是其秩:
1
2
3
len(stacked_threes.shape)
3
对您来说,致力于记忆和练习这些张量的行话 真的很重要:秩是张量中的轴数或尺寸数;形状是张量每个轴的大小。
答:小心,因为“维度”一词有时以两种方式使用。考虑一下,我们生活在“三维空间”,其中物理位置可以用 3-vector
v来描述。但根据PyTorch的说法,属性v.ndim(看起来肯定像v的“维度数”)等于1,而不是3!为什么?因为v是一个向量,是秩一的张量,这意味着它只有一个轴(即使该轴的长度为三)。换句话说,有时维度用于轴的大小(“空间是三维”);有时,它用于秩或轴数(“矩阵有两个维度”)。当混淆时,我发现将所有语句转换为秩、轴和长度术语很有帮助,这些术语是明确的术语。
我们也可以直接用 ndim 获得张量的秩:
1
2
3
stacked_threes.ndim
3
最后,我们可以计算出理想的3是什么样子的。我们使用 秩-3 张量的维度0的平均值来计算所有图像张量的平均值。这是对所有图像进行索引的维度。
换句话说,对于每个像素位置,这将计算该像素在所有图像上的平均值。结果将是每个像素位置的一个值。在这里:
1
2
mean3 = stacked_threes.mean(0)
show_image(mean3);
根据这个数据集,这是理想的数字3!(你可能不喜欢它,但这就是3号的样子。)你可以看到所有图像都同意应该是黑暗的地方非常黑,但在图像不一致的地方,它变得纤细和模糊。
让我们为7年代做同样的事情,但同时将所有步骤放在一起,以节省一些时间:
1
2
mean7 = stacked_sevens.mean(0)
show_image(mean7);
现在让我们选择一个任意的3,并测量它与我们“理想数字”的距离。
停止:停下来思考!:您如何计算特定图像与我们每个理想数字有多相似?记得离开这本书,在继续之前记下一些想法!研究表明,当你通过自己解决问题、实验和尝试新想法来参与学习过程时,回忆和理解会显著提高。
这里是一个样本3:
1
2
a_3 = stacked_threes[1]
show_image(a_3);
我们如何确定它与我们的理想3的距离?我们不能只是把这张图像的像素和理想数字之间的差异相加。一些差异将是积极的,而另一些差异将是负面的,这些差异将抵消,导致一些地方太暗,另一些地方太浅的图像可能会显示为与理想完全差异为零。那会误导人!
为了避免这种情况,数据科学家在这方面有两种主要测量距离的方法:
- 以差异绝对值的平均值(绝对值是用正值取代负值的函数)。这被称为平均绝对差值或L1范数。
- 取差异平方的平均值(使一切都是正数),然后取平方根(这会解开平方)。这被称为根平均平方误差(RMSE)或L2范数。
重要信息:忘记你的数学没关系:在这本书中,我们通常认为你已经完成了高中数学,并至少记住其中的一些……但每个人都会忘记一些事情!这完全取决于你碰巧在此期间有理由练习什么。也许你已经忘记了平方根是什么,或者它们是如何工作的。没问题!每当你遇到这本书没有充分解释的数学概念时,不要继续前进;相反,停下来查一下。确保您理解基本想法,它是如何工作的,以及我们可能使用它的原因。Khan Academy是刷新你理解力的最佳场所之一。
现在让我们试试这两个:
1
2
3
4
5
6
dist_3_abs = (a_3 - mean3).abs().mean()
dist_3_sqr = ((a_3 - mean3)**2).mean().sqrt()
dist_3_abs,dist_3_sqr
(tensor(0.1114), tensor(0.2021))
1
2
3
4
5
dist_7_abs = (a_3 - mean7).abs().mean()
dist_7_sqr = ((a_3 - mean7)**2).mean().sqrt()
dist_7_abs,dist_7_sqr
(tensor(0.1586), tensor(0.3021))
在这两种情况下,我们的3和“理想”3之间的距离都小于到理想7的距离。因此,在这种情况下,我们的简单模型将给出正确的预测。
PyTorch已经将这两个作为损失函数提供了。您可以在torch.nn.functional中找到这些,PyTorch团队建议将其导入为F(默认情况下,该名称在fastai中可用):
1
2
3
F.l1_loss(a_3.float(),mean7), F.mse_loss(a_3,mean7).sqrt()
(tensor(0.1586), tensor(0.3021))
这里mse代表平均平方误差,l1指的是平均绝对值的标准数学术语(在数学中,它被称为L1范数)。
S:直觉上,L1范数和平均平方误差(MSE)的区别在于,后者将比前者对更大的错误惩罚更大(并对小错误更宽容)。
J:当我第一次遇到这个“L1”的东西时,我抬头看看它到底是什么意思。我在谷歌上发现这是一个使用绝对值的矢量范数,所以查找矢量规范并开始读取:给定实数或复数字段F上的矢量空间V,V上的规范是一个非负值的任何函数p:V→[0,+∞),具有以下属性:对于所有?F和所有u,v?V,p(u + v)≤p(u) + p(v)…然后我停止了阅读。呃,我永远不会懂数学!我千次想。从那以后,我了解到,每当这些复杂的数学术语在实践中出现时,我都可以用一小部分代码替换它们!比如,L1损失仅等于(a-b)。abs().mean(),其中a和b是张量。我猜数学家的想法和我不一样……在这本书中,我会确保每次出现一些数学术语时,我都会给你一点它等同的代码,并以常识性的方式解释发生了什么。
我们刚刚完成了PyTorch张量的各种数学运算。如果您以前在NumPy中做过一些数字编程,您可能会识别这些与NumPy数组相似。让我们看看这两个非常重要的数据结构。
NumPy Arrays and PyTorch Tensors
NumPy是Python中使用最广泛的科学和数字编程库。它的功能和API与PyTorch的功能非常相似;然而,它不支持使用GPU或计算梯度,这两者对深度学习都至关重要。因此,在这本书中,我们将尽可能使用PyTorch张量而不是NumPy数组。
(请注意,fastai为NumPy和PyTorch添加了一些功能,以使它们彼此更相似。如果本书中的任何代码在您的计算机上不起作用,您可能会忘记在笔记本电脑的开头包含这样一行:from fastai.vision.all import *.)
但什么是数组和张量,你为什么要关注呢?
与许多语言相比,Python速度很慢。Python、NumPy或PyTorch中的任何快速内容都可能是用另一种语言(特别是C)编写(和优化)的编译对象的包装器。事实上,NumPy数组和PyTorch张量可以比使用纯Python快数千倍完成计算。
NumPy数组是一个多维数据表,包含所有类型相同的项目。由于这可以是任何类型,它们甚至可以是数组数组,最内部的数组可能有不同的大小——这被称为“jagged array.”。例如,我们所说的“multidimensional table”是指list(一个维度)、一个table 或 matrix(两个维度)、一个“table of table”或“cube”(三个维度),等等。如果这些项目都是某种简单的类型,如整数或浮点,那么NumPy将把它们存储在内存中,作为紧凑的C数据结构。这就是NumPy发光的地方。NumPy有各种各样的运算符和方法,可以以与优化的C相同的速度在这些紧凑结构上运行计算,因为它们是用优化的C编写的。
PyTorch张量几乎与NumPy数组相同,但有一个额外的限制,可以解锁一些额外的功能。它也是一样的,因为它也是一个多维数据表,所有项目都属于同一类型。然而,限制是张量不能只使用任何旧类型——它必须对所有组件使用单个基本数字类型。例如,PyTorch张量不能jagged。它总是一个有规律的多维矩形结构。
NumPy在这些结构上支持的绝大多数方法和运算符也由PyTorch支持,但PyTorch张量具有额外的功能。一个主要功能是这些结构可以在GPU上计算,在这种情况下,它们的计算将针对GPU进行优化,并可以运行得更快(给定许多值需要处理)。此外,PyTorch可以自动计算这些操作的导数,包括操作的组合。正如您将看到的,没有这种能力,就不可能在实践中进行深度学习。
S:如果你不知道什么是C,别担心,因为你根本不需要它。简而言之,与Python相比,这是一种低级(低级意味着更类似于计算机内部使用的语言)语言。为了在Python中编程时利用其速度,请尽可能避免编写循环,并将其替换为直接在数组或张量上的命令。
也许Python程序员需要学习的最重要的新编码技能是如何有效使用array/tensor API。我们稍后将在这本书中展示更多技巧,但以下是您目前需要了解的关键内容的摘要。
要创建数组或张量,请将list(或list of lists,list of lists of lists 等)传递给 array() 或 tensor():
1
2
3
data = [[1,2,3],[4,5,6]]
arr = array (data)
tns = tensor(data)
1
2
3
4
arr # numpy
array([[1, 2, 3],
[4, 5, 6]])
1
2
3
4
tns # pytorch
tensor([[1, 2, 3],
[4, 5, 6]])
接下来的所有操作都显示在张量上,但NumPy数组的语法和结果是相同的。
您可以选择一行(请注意,与Python中的列表一样,张量是从0开始索引的,因此1引用第二行/列):
1
2
3
tns[1]
tensor([4, 5, 6])
或列,通过使用 : 来指示所有第一轴(我们有时将 tensor/array 的 dimensions 称为轴):
1
2
3
tns[:,1]
tensor([2, 5])
您可以将这些与Python切片语法相结合,以选择行或列的一部分:
1
2
3
tns[1,1:3]
tensor([5, 6])
你可以使用诸如 +, -, *, / 的操作:
1
2
3
4
tns + 1
tensor([[2, 3, 4],
[5, 6, 7]])
张量有类型:
1
2
3
tns.type()
'torch.LongTensor'
并将根据需要自动更改类型,例如从 int 到 float:
1
2
3
4
tns*1.5
tensor([[1.5000, 3.0000, 4.5000],
[6.0000, 7.5000, 9.0000]])
那么,我们的基线模型好吗?要量化这一点,我们必须定义一个指标。
Computing Metrics Using Broadcasting
回想一下,指标是根据模型的预测和数据集中的正确标签计算的数字,目的是告诉我们模型有多好。例如,我们可以使用我们在上一节中看到的任一函数、平均平方误差或平均绝对误差,并将它们的平均值放在整个数据集中。然而,这两个数字都不是大多数人非常容易理解的数字;在实践中,我们通常使用准确性作为分类模型的指标。
正如我们所讨论的,我们希望在验证集上计算我们的指标。这是这样我们就不会无意中过拟合。对于我们在这里作为第一次尝试使用的像素相似性模型来说,这不是真正的风险,因为它没有训练的组件,但无论如何,我们将使用验证集来遵循正常实践,并为以后的第二次尝试做好准备。
为了获得验证集,我们需要从训练中完全删除一些数据,因此模型根本看不到它。事实证明,MNIST数据集的创建者已经为我们做了这件事。你还记得有个单独的目录 valid 吗?这就是这个目录的目的!
因此,首先,让我们从该目录中为我们的 3 和 7 创建张量。以下是我们将用来计算衡量我们首次尝试模型质量的度量的张量,该模型测量了与理想图像的距离:
1
2
3
4
5
6
7
8
9
10
valid_3_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'3').ls()])
valid_3_tens = valid_3_tens.float()/255
valid_7_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'7').ls()])
valid_7_tens = valid_7_tens.float()/255
valid_3_tens.shape,valid_7_tens.shape
(torch.Size([1010, 28, 28]), torch.Size([1028, 28, 28]))
养成边走边检查形状的习惯是件好事。在这里,我们看到两个张量,一个代表28×28大小的1010张图像 3的验证集,另一个代表28×28大小的1028张图像 7 的验证集。
我们最终想写一个函数 is_3 ,该函数将决定任意图像是 3 还是 7 。它将通过决定这个任意图像更接近我们两个“理想数字”中的哪一个来做到这一点。为此,我们需要定义一个距离的概念——即计算两张图像之间距离的函数。
我们可以编写一个简单的函数,使用与我们在最后一节中编写的表达式非常相似的表达式来计算平均绝对误差:
1
2
3
4
def mnist_distance(a,b): return (a-b).abs().mean((-1,-2))
mnist_distance(a_3, mean3)
tensor(0.1114)
这与我们之前为这两张图像之间的距离计算的值相同,理想 3 mean3 和任意样本3 a_3,它们都是形状为 [28,28] 的单图像张量。
但为了计算整体准确性指标,我们需要计算验证集中每张图像到理想3的距离。我们如何计算?我们可以在我们的验证集张量valid_3_tens中堆叠的所有单图像张量上写一个循环,该张量的形状为 [1010,28,28],代表1,010张图像。但有更好的方法。
当我们使用这个完全相同的距离函数时,发生了一些非常有趣的事情,该函数旨在比较两个单个图像,但作为表示 3 验证集的张量valid_3_tens 作为参数传递时:
1
2
3
4
5
valid_3_dist = mnist_distance(valid_3_tens, mean3)
valid_3_dist, valid_3_dist.shape
(tensor([0.1050, 0.1526, 0.1186, ..., 0.1122, 0.1170, 0.1086]),
torch.Size([1010]))
它没有抱怨形状不匹配,而是将每张图像的距离作为长度为1,010(我们验证集中的 3 的数量)的矢量(即秩-1张量)返回。那是怎么发生的?
再看看我们的函数 mnist_distance,你会发现我们在那里有减法(a-b)。神奇的诀窍是,当PyTorch试图在不同秩的两个张量之间执行简单的减法操作时,它将使用广播。也就是说,它将自动扩展秩较小的张量,使其大小与秩较大的张量相同。广播是一项重要功能,它使张量代码更容易编写。
在广播使两个参数张量具有相同的秩后,PyTorch将其通常的逻辑应用于同一秩的两个张量:它对两个张量的每个对应元素执行操作,并返回张量结果。例如:
1
2
3
tensor([1,2,3]) + tensor(1)
tensor([2, 3, 4])
因此,在这种情况下,PyTorch将表示单个图像的秩-2张量平均值视为同一图像的1010 份副本,然后从我们的验证集中的每个3减去每个副本。你希望这个张量有什么形状?在查看以下答案之前,请先尝试自己弄清楚:
1
2
3
(valid_3_tens-mean3).shape
torch.Size([1010, 28, 28])
我们正在计算28×28图像中每个图像的“理想3”和验证集中的1,010 个3之间的差异,结果形状为 [1010,28,28] 。
关于如何实施广播,有几个要点:
- PyTorch实际上不会复制
mean31010次。它假装它是那个形状的张量,但实际上没有分配任何额外的内存。 - 它用C进行整个计算(或者,如果您使用的GPU,在CUDA中,相当于GPU上的C),比纯Python快数万倍(GPU上快数百万倍!)。
在PyTorch中完成的所有广播和元素操作和功能都是如此。创建高效的PyTorch代码是您知道的最重要技术。
接下来在 mnist_distance 中,我们看到 abs。您现在可以猜测当应用于张量时,这会做什么。它将该方法应用于张量中的每个单个元素,并返回结果的张量(即它“在元素上”应用该方法)。因此,在这种情况下,我们将获得1010个绝对值矩阵。
最后,我们的函数调用 mean(-1,-2))。元组 (-1,-2) 代表一系列轴。在Python中,-1指的是最后一个元素,-2指的是倒数第二个元素。因此,在这种情况下,这告诉PyTorch,我们希望采用张量最后两个轴索引的值的平均范围。最后两个轴是图像的水平和垂直尺寸。在计算了最后两个轴的平均值后,我们只剩下第一个张量轴,该张量轴在我们的图像上索引,这就是为什么我们的最终尺寸是(1010)。换句话说,对于每张图像,我们平均了该图像中所有像素的强度。
我们将在整个这本书中学到更多关于广播的信息,并将定期练习。
我们可以使用 mnist_distance 使用以下逻辑来确定图像是否为3:如果相关数字与理想3之间的距离小于与理想7的距离,则为3。与所有PyTorch函数和运算符一样,此函数将自动进行广播和元素应用:
1
def is_3(x): return mnist_distance(x,mean3) < mnist_distance(x,mean7)
让我们在我们的示例案例中进行测试:
1
2
3
is_3(a_3), is_3(a_3).float()
(tensor(True), tensor(1.))
请注意,当我们将布尔响应转换为浮点数时,我们获得 1.0 表示True,0.0 表示False。多亏了广播,我们也可以在完整的3 验证集上进行测试:
1
2
3
is_3(valid_3_tens)
tensor([True, True, True, ..., True, True, True])
现在,我们可以计算准确性:
1
2
3
4
5
6
accuracy_3s = is_3(valid_3_tens).float() .mean()
accuracy_7s = (1 - is_3(valid_7_tens).float()).mean()
accuracy_3s,accuracy_7s,(accuracy_3s+accuracy_7s)/2
(tensor(0.9168), tensor(0.9854), tensor(0.9511))
这看起来是一个很好的开始!我们在 3 和 7 上的准确性都超过90%,我们已经看到了如何使用广播方便地定义指标。
但老实说:3 和 7 是外观非常不同的数字。到目前为止,我们只对10个可能的数字中的2个进行分类。因此,我们需要做得更好!
为了做得更好,也许是时候尝试一个能进行一些真正学习的系统了——也就是说,它可以自动修改自己以提高其性能。换句话说,是时候谈谈训练过程和SGD了。
Stochastic Gradient Descent (SGD)
你还记得我们在引用的亚瑟·塞缪尔描述机器学习的方式吗?
:假设我们安排了一些自动方法,从实际性能方面测试任何当前权重分配的有效性,并提供更改权重分配的机制,以最大限度地提高性能。我们不需要深入研究这样一个程序的细节,看看它可以完全自动化,也不需要看到这样编程的机器会从其经验中“学习”。
正如我们所讨论的,这是让我们拥有一个可以越来越好——可以学习的模型的关键。但我们的像素相似性方法并没有真正做到这一点。我们没有任何类型的权重分配,也没有基于测试权重分配有效性的任何改进方法。换句话说,我们无法通过修改一组参数来真正改进像素相似性方法。为了利用深度学习的力量,我们首先必须以亚瑟·塞缪尔描述的方式代表我们的任务。
我们不是试图找到图像和“理想图像”之间的相似之处,而是可以查看每个像素,并为每个像素想出一组权重,这样最高权重与特定类别中最有可能是黑色的像素相关联。例如,右下角的像素不太可能在7时激活,因此它们应该在7时的重量较低,但它们可能会在8时激活,因此它们应该在8时的重量很高。这可以表示为每个可能类别的函数和权重值集——例如成为数字8的概率:
1
def pr_eight(x, w): return (x*w).sum()
在这里,我们假设 x 是图像,以矢量表示——换句话说,所有行都从头到尾堆叠成一条长线。我们假设权重是一个矢量w。如果我们有这个函数,那么我们只需要一些方法来更新权重,使它们变得更好一点。通过这种方法,我们可以多次重复这一步骤,使权重越来越好,直到它们尽可能好。
我们希望找到矢量 w 的特定值,这些值导致我们函数的结果在实际上为 8 的图像中为高,而在那些不是 8 的图像中为低。搜索最佳矢量w是搜索识别 8 的最佳函数的一种方式。(由于我们尚未使用深度神经网络,我们受到函数实际功能的限制——我们将在本章后面修复该约束。)
更具体地说,以下是我们将需要的步骤,将此函数转换为机器学习分类器:
- 初始化权重
- 对于每张图像,使用这些权重来预测它似乎是3还是7。
- 基于这些预测,计算模型有多好(其损失)。
- 计算梯度,衡量每个权重,改变该权重将如何改变损失
- 根据该计算步骤(即更改)所有权重。
- 回到第2步,然后重复这个过程。
- 迭代,直到您决定停止训练过程(例如,因为模型足够好,或者您不想再等了)。
这七个步骤是训练所有深度学习模型的关键。事实证明,这种深度学习完全依赖于这些步骤,这非常令人惊讶和违反直觉。令人惊讶的是,这个过程可以解决如此复杂的问题。但是,正如您将看到的,它确实如此!
这七个步骤都有很多不同的方法,我们将在这本书的其余部分学习它们。这些细节对深度学习从业者有很大影响,但事实证明,对每个细节的一般方法通常遵循一些基本原则。以下是一些准则:
- 初始化::我们将参数初始化为随机值。这听起来可能令人惊讶。当然,我们还可以做出其他选择,例如将它们初始化为该类别激活像素的百分比——但由于我们已经知道我们有一个例程来改进这些权重,事实证明,仅从随机权重开始效果很好。
- 损失:这就是塞缪尔在谈到从实际表现的角度测试当前任何权重分配的有效性时所说的。我们需要一些函数,如果模型的性能良好,它会返回一个小的数字(标准方法是将小损失视为好,大损失视为坏,尽管这只是一个惯例)。
- 步骤:确定权重是应该增加一点还是减少一点的简单方法是尝试一下:增加一点权重,看看损失是上升还是下降。一旦你找到了正确的方向,你就可以多一点,少一点,直到你找到一个效果良好的数量。然而,这很慢!正如我们将看到的,微积分的魔力使我们能够直接计算每个权重的改变方向和大致的大小,而无需尝试所有这些小变化。这样做的方法是计算梯度。这只是性能优化,我们也会使用较慢的手动流程获得完全相同的结果。
- 停止:一旦我们决定训练模型的几个时代(前面的列表中对此提出了一些建议),我们就会应用该决定。这就是适用该决定的地方。对于我们的数字分类器,我们会继续训练,直到模型的准确性开始恶化,或者我们没时间了。
在将这些步骤应用于我们的图像分类问题之前,让我们在更简单的情况下说明它们是什么样子的。首先,我们将定义一个非常简单的函数,二次函数——让我们假设这是我们的损失函数,x是函数的权重参数:
1
def f(x): return x**2
以下是该函数的图表:
1
plot_function(f, 'x', 'x**2')
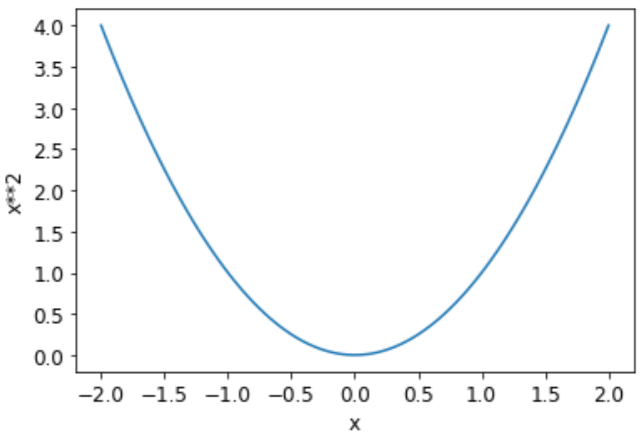
我们之前描述的步骤顺序从为参数选择一些随机值并计算损失值开始:
1
2
plot_function(f, 'x', 'x**2')
plt.scatter(-1.5, f(-1.5), color='red');
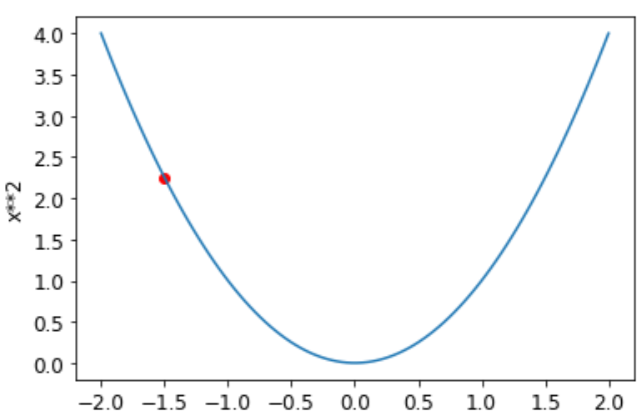
现在,我们看看如果我们增加或减少一点参数——调整——会发生什么。这仅仅是特定点的斜率:
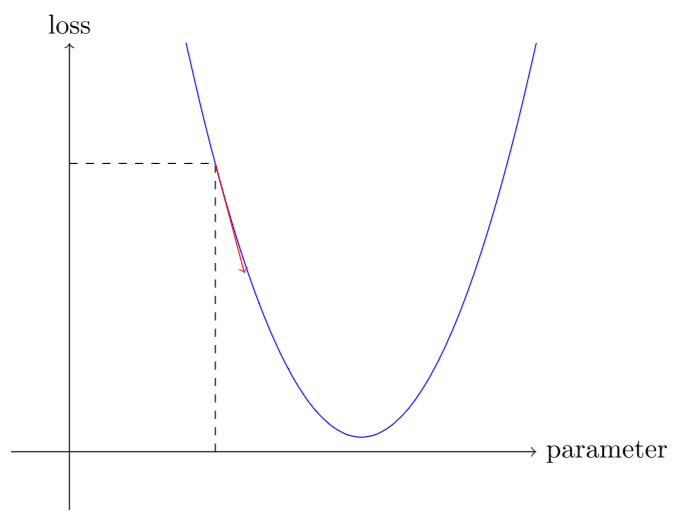
我们可以在斜坡方向上稍微改变一下权重,再次计算我们的损失和调整,然后重复几次。最终,我们将到达曲线的最低点:
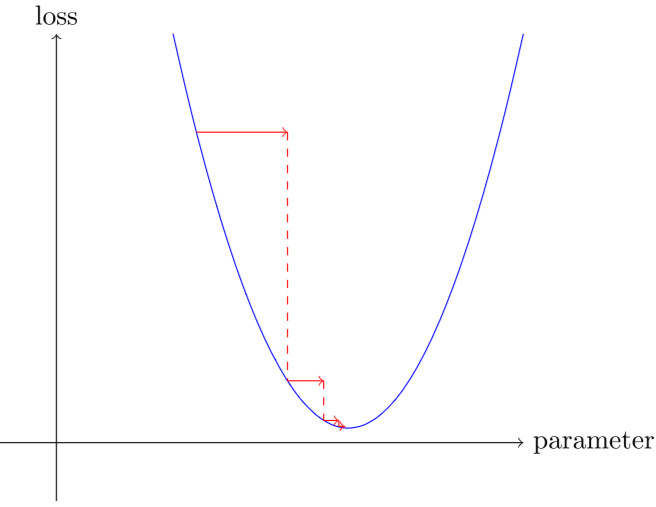
这个基本想法可以追溯到艾萨克·牛顿,他指出我们可以以这种方式优化任意函数。无论我们的功能变得多么复杂,这种梯度下降的基本方法都不会显著改变。我们在本书后面看到的唯一小变化是一些方便的方法,通过找到更好的步骤来加快速度。
Calculating Gradients
一个神奇的步骤是我们计算梯度。正如我们提到的,我们使用微积分作为性能优化;它允许我们更快地计算当我们向上或向下调整参数时,我们的损失是上升还是下降。换句话说,梯度将告诉我们,为了使我们的模型变得更好,我们必须改变每个权重。
您可能还记得,从高中微积分课上,函数的导数告诉你其参数的变化将在多大程度上改变其结果。如果没有,别担心,一旦高中毕业,我们很多人就会忘记微积分!但在继续之前,你必须对导数是什么有一些直观的理解,所以如果这一切在你的脑海中都非常模糊,那就去汗学院完成基础导数课程。你不必自己知道如何计算它们,你只需要知道什么是导数。
关于导数的关键是:对于任何函数,例如我们在上一节中看到的二次函数,我们可以计算其导数。导数是另一个函数。它计算变化,而不是值。例如,值3处二次函数的导数告诉我们值3处函数的变化有多快。更具体地说,您可能还记得梯度被定义为上升/运行,即函数值的变化除以参数值的变化。当我们知道我们的功能将如何变化时,我们就知道我们需要做些什么来缩小它。这是机器学习的关键:有办法更改函数的参数,使其更小。微积分为我们提供了一个计算快捷方式,即导数,它允许我们直接计算函数的梯度。
需要注意的一件重要事情是,我们的函数有很多权重,我们需要调整,所以当我们计算导数时,我们不会得到一个数字,而是很多——每个权重的梯度。但这在数学上没有什么棘手的;你可以计算一个权重的导数,并将所有其他权重视为常数,然后对彼此的权重冲复。这就是计算每个权重的所有梯度的方法。
我们刚才提到,你不必自己计算任何梯度。那怎么可能呢?令人惊讶的是,PyTorch能够自动计算几乎所有函数的导数!此外,它做得很快。大多数时候,它将至少与您手动创建的任何导数函数一样快。让我们看看一个例子。
1
xt = tensor(3.).requires_grad_()
注意特殊方法 require_grad_ ?这是我们用来告诉PyTorch的神奇咒语,我们希望以该值计算该变量的梯度。它本质上是在标记变量,因此PyTorch将记住跟踪如何计算其他变量的梯度,直接计算您将要求的变量。
现在我们用这个值计算我们的函数。请注意,PyTorch如何不仅打印计算值,还要打印梯度函数,它将在需要时用于计算我们的梯度:
1
2
3
4
yt = f(xt)
yt
tensor(9., grad_fn=<PowBackward0>)
最后,我们告诉PyTorch为我们计算梯度:
1
yt.backward()
这里的“backward”是指反向传播,这是计算每层导数过程的名称。当我们从头开始计算深层神经网的梯度时。这被称为网络的“反向传播”,而不是计算激活的“前向传播”。如果 backward 只是被称为 calculate_grad的话,可能会更加容易理解,但深度学习的人真的喜欢尽可能地添加行话!
我们现在可以通过检查张量的梯度属性来查看梯度:
1
2
3
xt.grad
tensor(6.)
如果您还记得高中的微积分规则,x**2 的导数是 2*x ,我们有 x=3,所以梯度应该是 2*3=6 ,这就是PyTorch为我们计算的!
现在,我们将重复前面的步骤,但我们的函数有一个向量参数:
1
2
3
4
xt = tensor([3.,4.,10.]).requires_grad_()
xt
tensor([ 3., 4., 10.], requires_grad=True)
我们将向函数添加 `sum,以便它能够接受向量(即秩-1张量),并返回标量(即秩-0张量):
1
2
3
4
5
6
def f(x): return (x**2).sum()
yt = f(xt)
yt
tensor(125., grad_fn=<SumBackward0>)
正如我们所期望的那样,我们的梯度是 2*xt !
1
2
3
4
yt.backward()
xt.grad
tensor([ 6., 8., 20.])
梯度只告诉我们函数的斜率,它们实际上并没有确切地告诉我们调整参数的程度。但它让我们知道了多远;如果斜率很大,那么这可能意味着我们有更多的调整要做,而如果斜率很小,这可能意味着我们接近了最佳值。
Stepping With a Learning Rate
根据梯度的值决定如何更改参数是深度学习过程的重要组成部分。几乎所有方法都从梯度乘以一些小数字的基本思想开始,称为学习率(LR)。学习率通常在0.001到0.1之间,尽管它可以是任何东西。通常,人们只需尝试一些,并在训练后找到最佳模型来选择学习率(我们将在本书后面向您展示一种更好的方法,称为学习率查找器)。选择学习率后,您可以使用以下简单函数调整参数:
\[w -= \text{gradient}(w) * lr\]如果你选择的学习率太低,这可能意味着必须做很多步骤。
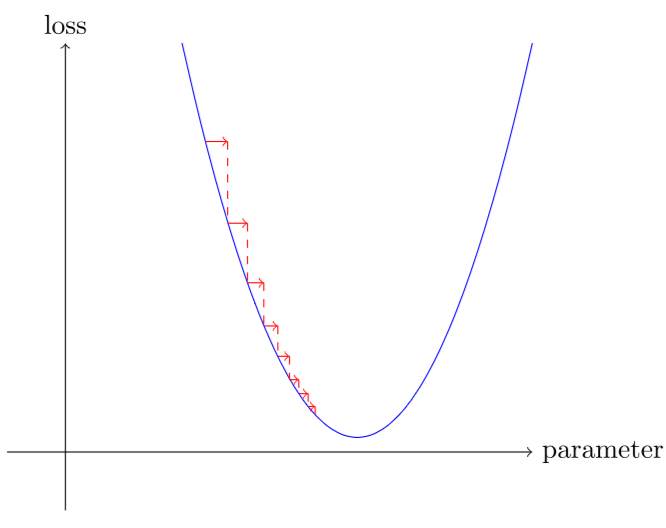
但选择过高的学习率甚至更糟——这实际上可能导致损失恶化:
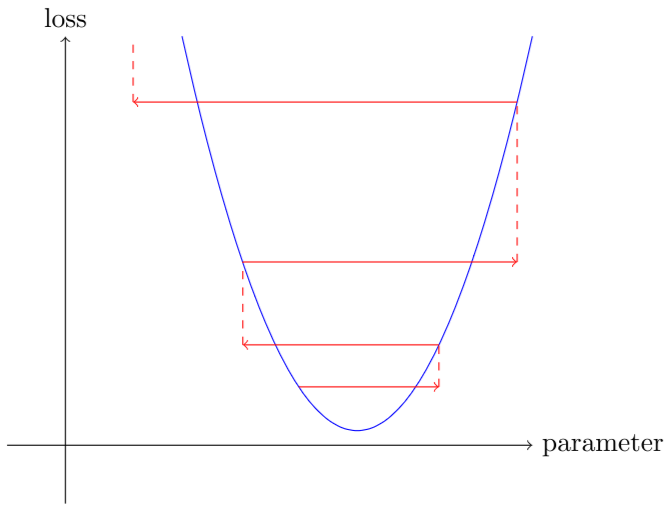
如果学习率太高,它也可能“反弹”,而不是发散;展示了这是如何采取许多步骤成功训练的结果。
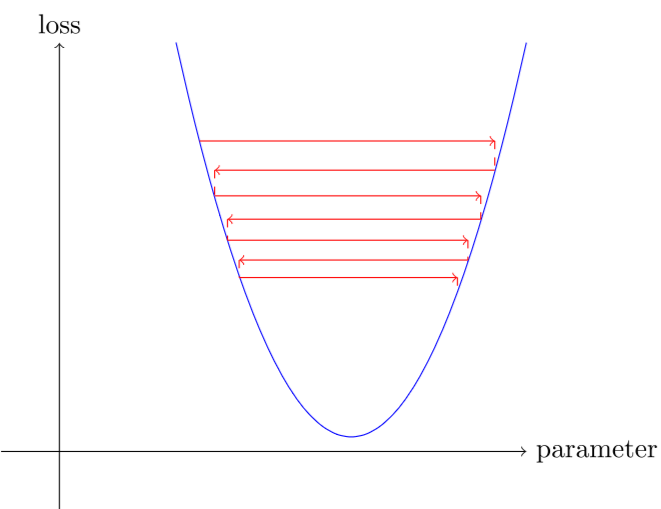
现在,让我们在端到端示例中应用所有这些。
An End-to-End SGD Example
我们已经看到了如何使用梯度来找到最小值。现在是时候看看SGD示例了,看看如何利用找到最小值来训练模型以更好地适应数据了。
让我们从一个简单、合成的示例模型开始。想象一下,当你过山车越过驼峰顶时,你正在测量过山车的速度。它会快速启动,然后在上山时变慢;在顶部会最慢,然后下坡时会再次加速。你想建立一个速度随时间变化的模型。如果您每秒手动测量速度,持续20秒,它可能如下所示:
1
2
3
time = torch.arange(0,20).float(); time
tensor([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11., 12., 13., 14., 15., 16., 17., 18., 19.])
1
2
speed = torch.randn(20)*3 + 0.75*(time-9.5)**2 + 1
plt.scatter(time,speed);
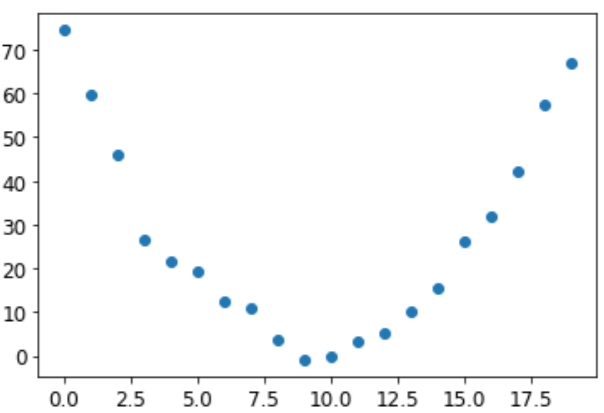
我们添加了一点随机噪音,因为手动测量东西并不精确。这意味着回答以下问题并不容易:训练的速度是多少?使用SGD,我们可以尝试找到一个与我们观察结果匹配的函数。我们不能考虑每个可能的函数,所以让我们猜测它是二次函数;即形式 a*(time**2)+(b*time)+c 的函数。
我们希望明确区分函数的输入及其参数。因此,让我们在一个参数中收集参数,从而分离函数签名中的输入、t 和参数 params:
1
2
3
def f(t, params):
a,b,c = params
return a*(t**2) + (b*t) + c
换句话说,我们已将找到最适合数据的最佳可想象的函数的问题限制在找到最佳二次函数上。这大大简化了问题,因为每个二次函数都完全由三个参数a、b和c定义。因此,要找到最佳二次函数,我们只需要为a、b和c找到最佳值。
如果我们可以为二次函数的三个参数解决这个问题,我们将能够对参数更多的其他更复杂的函数(例如神经网络)应用相同的方法。让我们先找到 f 的参数,然后回来用神经网络为MNIST数据集做同样的事情。
我们需要首先定义我们所说的“最佳”是什么意思。我们通过选择损失函数来精确地定义这一点,该函数将返回基于预测和目标的值,其中函数的较低值对应于“更好的”预测。对于连续数据,通常使用平均平方误差:
1
def mse(preds, targets): return ((preds-targets)**2).mean().sqrt()
现在,让我们完成我们的7步流程。
Step 1: Initialize the parameters
首先,我们将参数初始化为随机值,并告诉PyTorch,我们希望使用 require_grad_ 跟踪它们的梯度:
1
params = torch.randn(3).requires_grad_()
1
2
#hide
orig_params = params.clone()
Step 2: Calculate the predictions
接下来,我们计算预测:
1
preds = f(time, params)
让我们创建一个小函数,看看我们的预测离目标有多近,并看看:
1
2
3
4
5
def show_preds(preds, ax=None):
if ax is None: ax=plt.subplots()[1]
ax.scatter(time, speed)
ax.scatter(time, to_np(preds), color='red')
ax.set_ylim(-300,100)
1
show_preds(preds)
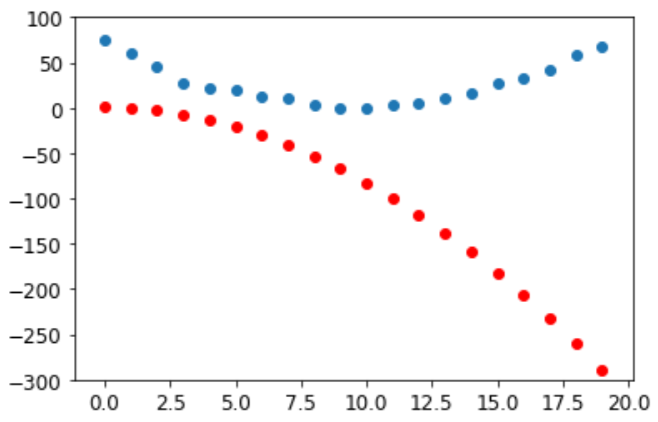
这看起来不是很接近——我们的随机参数表明过山车最终会倒退,因为我们的速度是负的!
Step 3: Calculate the loss
我们按以下方式计算损失:
1
2
3
4
loss = mse(preds, speed)
loss
tensor(25823.8086, grad_fn=<MeanBackward0>)
我们现在的目标是改善它。要做到这一点,我们需要知道梯度。
Calculate the gradients
下一步是计算梯度。换句话说,计算参数需要如何更改的近似值:
1
2
3
4
loss.backward()
params.grad
tensor([-53195.8594, -3419.7146, -253.8908])
1
2
3
params.grad * 1e-5
tensor([-0.5320, -0.0342, -0.0025])
我们可以使用这些梯度来改进我们的参数。我们需要选择一个学习率(我们将在下一章中讨论在实践中如何做到这一点;目前我们只使用1e-5或0.00001):
1
2
3
params
tensor([-0.7658, -0.7506, 1.3525], requires_grad=True)
Step 5: Step the weights.
现在我们需要根据我们刚刚计算的梯度更新参数:
1
2
3
lr = 1e-5
params.data -= lr * params.grad.data
params.grad = None
a:理解这一点取决于对近代历史的记忆。为了计算梯度,我们回调损失。但这种损失本身是由mse计算的,mse反过来将preds作为输入,并使用f作为输入参数计算,这是我们最初调用require_grads_的对象——这是现在允许我们对损失向后调用的原始调用。这个函数链调用代表了函数的数学组成,这使得PyTorch能够在引擎下使用微积分的链规则来计算这些梯度。
让我们看看损失是否有所改善:
1
2
3
4
preds = f(time,params)
mse(preds, speed)
tensor(5435.5366, grad_fn=<MeanBackward0>)
我们绘图来看一下:
1
show_preds(preds)
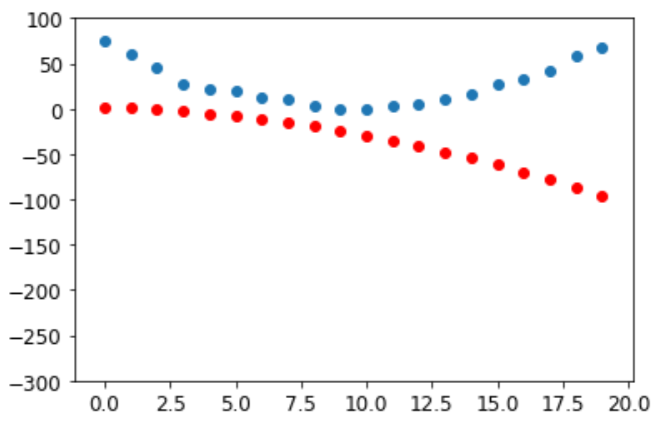
我们需要重复几次,所以我们将创建一个函数来应用 step:
1
2
3
4
5
6
7
8
def apply_step(params, prn=True):
preds = f(time, params)
loss = mse(preds, speed)
loss.backward()
params.data -= lr * params.grad.data
params.grad = None
if prn: print(loss.item())
return preds
Step 6: Repeat the process
现在我们迭代。通过循环和执行许多改进,我们希望取得良好结果:
1
2
3
4
5
6
7
8
9
10
11
12
for i in range(10): apply_step(params)
5435.53662109375
1577.4495849609375
847.3780517578125
709.22265625
683.0757446289062
678.12451171875
677.1839599609375
677.0025024414062
676.96435546875
676.9537353515625
1
2
#hide
params = orig_params.detach().requires_grad_()
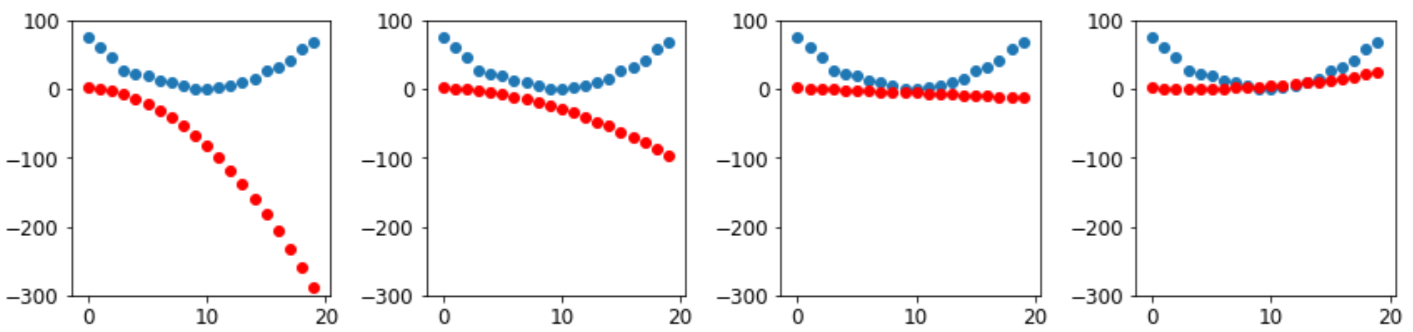
正如我们所希望的那样,损失正在下降!但只看这些损失数字就掩盖了一个事实,即在寻找最佳二次函数的路上,每个迭代代表着一个完全不同的二次函数。如果我们没有打印丢失函数,而是在每个步骤上绘制该函数,我们可以看到这个过程。然后,我们可以看到形状如何接近我们数据的最佳二次函数:
1
2
3
_,axs = plt.subplots(1,4,figsize=(12,3))
for ax in axs: show_preds(apply_step(params, False), ax)
plt.tight_layout()
Step 7: stop
我们只是决定在10个 epoch 之后地停下来。在实践中,正如我们所讨论的那样,我们将关注训练和验证损失以及我们的指标,以决定何时停止。
Summarizing Gradient Descent
总之,在开头,我们的模型的权重可以是随机的(从头开始训练),也可以来自预训练的模型(迁移学习)。在第一种情况下,我们将从输入中获得的输出与我们想要的东西无关,即使在第二种情况下,预训练模型也很有可能不擅长我们所针对的具体任务。因此,模型需要学习更好的权重。
我们首先使用损失函数将模型给我们的输出与我们的目标进行比较(我们已经标记了数据,所以我们知道模型应该给出什么结果),该函数返回一个我们希望通过提高权重来尽可能低的数字。为此,我们从训练集中提取一些数据项(如图像),并将其输入我们的模型。我们使用损失函数比较相应的目标,我们得到的分数告诉我们我们的预测有多错误。然后我们稍微改变一下权重,让它稍微好一点。
为了找到如何改变权重以使损失变得更好,我们使用微积分来计算梯度。(事实上,我们让PyTorch为我们做这件事!)让我们考虑一个类比。想象一下,你的车停在最低点,迷失在山里。要找到回到它的道路,你可能会随机地徘徊,但这可能没有多大帮助。既然你知道你的车处于最低点,你最好下坡。通过总是朝着最陡峭的下坡方向迈出一步,你最终应该到达目的地。我们使用梯度的大小(即斜坡的陡度)来告诉我们要迈出的一步有多大;具体来说,我们将梯度乘以我们选择的称为学习率的数字来决定步长。然后我们迭代,直到到达最低点,也就是我们的停车场,然后我们可以停下来。
除了损失函数外,我们刚刚看到的所有信息都可以直接传输到MNIST数据集中。现在让我们看看如何定义一个好的训练目标。
The MNIST Loss Function
我们已经有了独立的变量x——这些是图像本身。我们将把它们全部连接成一个张量,并将它们从矩阵列表(秩-3张量)更改为矢量列表(秩-2张量)。我们可以使用 view 来做到这一点, view 是一种PyTorch方法,可以在不更改张量内容的情况下更改张量的形状。-1是一个特殊的参数来查看,这意味着“使这个轴尽可能大,以适应所有数据”:
1
train_x = torch.cat([stacked_threes, stacked_sevens]).view(-1, 28*28)
我们需要每个图像的标签。我们将使用1用于3,0用于7:
1
2
3
4
train_y = tensor([1]*len(threes) + [0]*len(sevens)).unsqueeze(1)
train_x.shape,train_y.shape
(torch.Size([12396, 784]), torch.Size([12396, 1]))
PyTorch中的 Dataset 在索引时需要返回元组 (x,y) 。Python提供了一个 zip 函数,当与 list 相结合时,该函数提供了获取此功能的简单方法:
1
2
3
4
5
dset = list(zip(train_x,train_y))
x,y = dset[0]
x.shape,y
(torch.Size([784]), tensor([1]))
1
2
3
valid_x = torch.cat([valid_3_tens, valid_7_tens]).view(-1, 28*28)
valid_y = tensor([1]*len(valid_3_tens) + [0]*len(valid_7_tens)).unsqueeze(1)
valid_dset = list(zip(valid_x,valid_y))
现在我们需要每个像素的(最初是随机的)权重(这是我们七步过程中的初始化步骤):
1
def init_params(size, std=1.0): return (torch.randn(size)*std).requires_grad_()
1
weights = init_params((28*28,1))
函数 weights*pixels 不够灵活——当像素等于0时,它总是等于0(即它的拦截是0)。你可能从高中数学中记得,一行的公式是 y=w*x+b ;我们仍然需要 b。我们也会将其初始化为随机数字:
1
bias = init_params(1)
在神经网络中,方程 y=w*x+b 中的w称为权重,b称为偏置。权重和偏差共同构成了参数。
行话:参数:模型的权重和偏差。权重是
w*x+b方程中的w,偏差是该方程中的b。
我们现在可以计算一个图像的预测:
1
2
3
(train_x[0]*weights.T).sum() + bias
tensor([20.2336], grad_fn=<AddBackward0>)
虽然我们可以使用Python for loop来计算每个图像的预测,但这会非常缓慢。由于Python循环不会在GPU上运行,并且Python通常是循环的慢语言,因此我们需要使用更高级别的函数在模型中尽可能多地表示计算。
在这种情况下,有一个非常方便的数学运算,可以计算矩阵的每一行 w*x ——它被称为矩阵乘法。下图显示了矩阵乘法的样子。
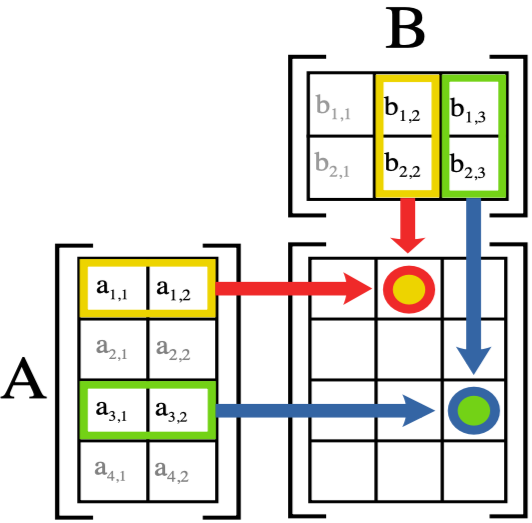
在Python中,矩阵乘法用@运算符表示。让我们试试:
1
2
3
4
5
6
7
8
9
10
11
def linear1(xb): return xb@weights + bias
preds = linear1(train_x)
preds
tensor([[20.2336],
[17.0644],
[15.2384],
...,
[18.3804],
[23.8567],
[28.6816]], grad_fn=<AddBackward0>)
正如我们预期的那样,第一个元素与我们之前计算的相同。这个方程,b batch@weights + bias,是任何神经网络的两个基本方程之一(另一个是激活函数,我们稍后会看到)。
让我们检查一下我们的准确性。要决定输出是代表3还是7,我们只需检查它是否大于0.5,这样我们就可以计算每个项目的准确性(使用广播,所以没有循环!):
1
2
3
4
5
6
7
8
9
10
corrects = (preds>0.5).float() == train_y
corrects
tensor([[ True],
[ True],
[ True],
...,
[False],
[False],
[False]])
1
2
3
corrects.float().mean().item()
0.4912068545818329
现在让我们看看其中一个权重的一个小变化的准确性变化是什么:
1
weights[0] *= 1.0001
1
2
3
4
preds = linear1(train_x)
((preds>0.0).float() == train_y).float().mean().item()
0.4912068545818329
正如我们所看到的,我们需要梯度来改进使用SGD的模型,为了计算梯度,我们需要一些表示模型有多好的损失函数。这是因为梯度是衡量损失函数如何随着权重的小调整而变化的尺度。
因此,我们需要选择一个损失函数。显而易见的方法是使用准确性(这是我们的指标)作为我们的损失函数。在这种情况下,我们将计算每张图像的预测,收集这些值以计算总体准确性,然后计算每个权重相对于该整体准确性的梯度。
不幸的是,我们这里有一个重大的技术问题。函数的梯度是它的斜率或陡度,可以定义为运行后的上升——即函数的值上升或下降程度除以我们更改输入的程度。我们可以用数学写成:(y_new - y_old)/(x_new - x_old)。当 x_new 与 x_old 非常相似时,这给了我们一个很好的梯度近似值,这意味着它们的差异很小。但只有当预测从3更改为7时,准确性才会发生变化,反之亦然。问题在于,权重从x_old 到 x_new 的微小变化不太可能导致任何预测发生变化,因此(y_new - y_old) 几乎总是0。换句话说,梯度几乎到处都是0。
权重值的很小变化通常实际上根本不会改变准确性。这意味着使用准确性作为损失函数是没有用的——如果我们这样做了,大多数时候我们的梯度实际上将是0,模型将无法从这个数字中学习。
S:从数学角度来看,准确性是一个几乎在所有地方都是恒定函数(阈值0.5除外),因此其导数几乎在所有地方都是零(阈值是无限)。然后,这给出了0或无限的梯度,这对更新模型毫无用处。
相反,我们需要一个损失函数,当我们的权重导致略好的预测时,它会给我们略好一点的损失。那么,“稍微好的预测”到底是什么样子的呢?好吧,在这种情况下,这意味着如果正确答案是3,分数会更高一点,或者如果正确答案是7,分数会更低一点。
现在让我们写这样一个函数。它采取什么形式?
损失函数接收的不是图像本身,而是来自模型的预测。让我们对0到1之间的值进行一个参数,其中每个值都是图像为3的预测。它是一个矢量(即秩-1张量),对所有图像索引。
损失函数的目的是测量预测值和真实值之间的差异——即目标(又称标签)。让我们做另一个参数,trgts,值为0或1,可以判断图像是否真的是3。它还是一个矢量(即另一个秩-1的张量),对所有图像索引。
因此,例如,假设我们有三张我们知道的图像是3、7和3。假设我们的模型高度自信(0.9)预测第一个是3,略微自信(0.4)第二个是7,一般自信(0.2),但错误的是,最后一个是7。这意味着我们的损失函数将接收这些值作为其输入:
1
2
trgts = tensor([1,0,1])
prds = tensor([0.9, 0.4, 0.2])
以下是衡量预测和目标之间距离的损失函数的首次尝试:
1
2
def mnist_loss(predictions, targets):
return torch.where(targets==1, 1-predictions, predictions).mean()
我们正在使用一个新的函数,torch.where(a,b,c)。这该函数的作用相同 [b[i] if a[i] else c[i] for i in range(len(a))],除了它以C/CUDA速度在张量上工作。在普通英语中,这个函数将测量每个预测与1(如果应该是1)的距离,如果应该是0,它将与0的距离有多远,然后将测量所有这些距离的平均值。
注意:阅读文档:了解这样的PyTorch函数很重要,因为Python中的张量循环以Python速度而不是C/CUDA速度运行!立即尝试运行help(torch.where)以阅读此函数的文档,或者更好的是,在PyTorch文档网站上查找它。
让我们来试一下我们的 prds 和 trgts:
1
2
3
torch.where(trgts==1, 1-prds, prds)
tensor([0.1000, 0.4000, 0.8000])
您可以看到,当预测更准确、准确预测更自信(绝对值更高)和预测不那么自信时,此函数返回的数字更低。在PyTorch中,我们总是假设损失函数的较低值更好。由于我们需要最终损失的标量,mnist_loss使用上一个张量的平均值:
1
2
3
mnist_loss(prds,trgts)
tensor(0.4333)
例如,如果我们将一个“错误”目标的预测从0.2更改为0.8,损失将下降,这表明这是一个更好的预测:
1
2
3
mnist_loss(tensor([0.9, 0.4, 0.8]),trgts)
tensor(0.2333)
目前定义的 mnist_loss 的一个问题是,它假设预测总是在0到1之间。那么,我们需要确保情况确实如此!碰巧的是,有一个函数可以做到这一点——让我们看看。
Sigmoid
sigmoid 函数总是输出0到1之间的数字。它的定义如下:
1
def sigmoid(x): return 1/(1+torch.exp(-x))
Pytorch为我们定义了一个加速版本,所以我们真的不需要自己的版本。这是深度学习中的一个重要函数,因为我们通常希望确保值在0到1之间。
1
plot_function(torch.sigmoid, title='Sigmoid', min=-4, max=4)
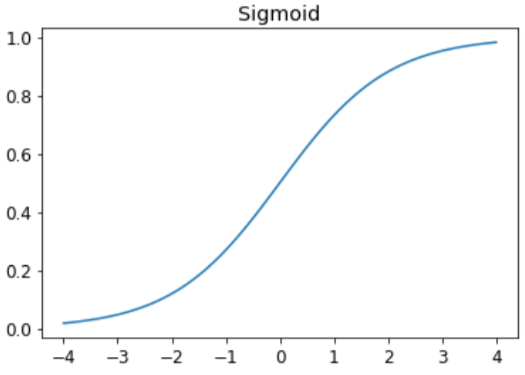
如您所见,它接受任何输入值,无论是正值还是负值,其输出值在0到1之间。这也是一条只上升的平滑曲线,这使得SGD更容易找到有意义的梯度。
让我们更新 mnist_loss,首先将 sigmoid 应用于输入:
1
2
3
def mnist_loss(predictions, targets):
predictions = predictions.sigmoid()
return torch.where(targets==1, 1-predictions, predictions).mean()
现在即使预测不在0到1之间,我们的损失函数也会起作用。更高的预测对应着更高的置信度。
在定义了损失函数后,现在是总结我们这样做的原因的好时机。毕竟,我们已经有一个指标,即准确性。那么,我们为什么要定义损失呢?
关键区别在于,该指标是为了推动人类的理解,而损失是为了推动自动化学习。为了推动自动化学习,损失必须是一个具有导数的函数。它不能有大平坦的部分和大跳跃,但必须相当光滑。这就是为什么我们设计了一个损失函数,以应对置信水平的微小变化。这一要求意味着,有时它并不真正反映我们试图实现的目标,而是我们真正目标和可以使用其梯度优化的功能之间的妥协。损失函数是为我们数据集中的每个项目计算的,然后在 epoch 结束时,损失值都是平均的,并报告 epoch 的总体平均值。
另一方面,指标是我们真正关心的数字之一。这些是每个 epoch 末尾打印的值,告诉我们我们的模型到底做得怎么样。在判断模型的性能时,重要的是我们要学会关注这些指标,而不是损失。
SGD and Mini-Batches
现在我们有一个适合驱动SGD的损失函数,我们可以考虑学习过程下一阶段涉及的一些细节,即根据梯度更改或更新权重。这被称为优化步骤。
为了采取优化步骤,我们需要计算一个或多个数据项的损失。我们应该用多少?我们可以为整个数据集计算它,并取平均值,也可以为单个数据项计算它。但两者都不理想。为整个数据集计算它需要很长时间。为单个样本计算它不会使用太多信息,因此会导致非常不精确和不稳定的梯度。也就是说,您将难以更新权重。
因此,我们在两者之间达成妥协:我们一次计算几个数据项的平均损失。这被称为小批量。小批量处理中的数据项数量称为批处理大小。更大的批处理大小意味着您将从丢失函数中获得更准确、更稳定的数据集梯度估计,但这需要更长的时间,并且您将在每个epoch 处理更少的小批量。选择一个好的批量大小是您作为深度学习从业者需要做出的决定之一,以快速准确地训练您的模型。我们将在整个书中讨论如何做出这个选择。
使用小批量处理而不是计算单个数据项的梯度的另一个良好原因是,在实践中,我们几乎总是在GPU等加速器上进行训练。这些加速器只有在一次有很多工作要做时才能表现良好,所以如果我们能给他们很多数据项来处理,那会很有帮助。使用小批量是做到这一点的最佳方式之一。然而,如果您给他们的数据太多,无法同时处理,它们就会耗尽内存——让GPU满意也很难!
关于数据增强的讨论中所看到的,如果我们能在训练期间改变样本,我们会得到更好的泛化性。我们可以改变的一件简单而有效的事情是,我们在每个小批量中放置了哪些数据项。相反,我们通常做的不是简单地按每个epoch顺序枚举我们的数据集,而是在我们创建小批量之前,在每个 epoch 上随机随机洗牌。PyTorch和fastai提供了一个为您进行洗牌和小批处理排序的类,称为DataLoader。
DataLoader 可以接收任何Python集合,并将其转换为多个批次的迭代器,例如:
1
2
3
4
5
6
7
coll = range(15)
dl = DataLoader(coll, batch_size=5, shuffle=True)
list(dl)
[tensor([ 3, 12, 8, 10, 2]),
tensor([ 9, 4, 7, 14, 5]),
tensor([ 1, 13, 0, 6, 11])]
为了训练模型,我们不仅想要任何Python集合,还需要一个包含独立变量和依赖变量(即模型的输入和目标)的集合。在PyTorch中,包含独立变量和因变量元组的集合称为数据集。以下是一个极其简单的数据集的例子:
1
2
3
4
ds = L(enumerate(string.ascii_lowercase))
ds
(#26) [(0, 'a'),(1, 'b'),(2, 'c'),(3, 'd'),(4, 'e'),(5, 'f'),(6, 'g'),(7, 'h'),(8, 'i'),(9, 'j')...]
当我们将 Dataset 传递给 DataLoader 时,我们将返回许多小批量,这些小批量本身就是代表独立变量和依赖变量批处理的张量元组:
1
2
3
4
5
6
7
8
dl = DataLoader(ds, batch_size=6, shuffle=True)
list(dl)
[(tensor([17, 18, 10, 22, 8, 14]), ('r', 's', 'k', 'w', 'i', 'o')),
(tensor([20, 15, 9, 13, 21, 12]), ('u', 'p', 'j', 'n', 'v', 'm')),
(tensor([ 7, 25, 6, 5, 11, 23]), ('h', 'z', 'g', 'f', 'l', 'x')),
(tensor([ 1, 3, 0, 24, 19, 16]), ('b', 'd', 'a', 'y', 't', 'q')),
(tensor([2, 4]), ('c', 'e'))]
我们现在准备使用SGD为模型编写第一个训练循环!
Putting It All Together
在代码中,我们的流程将在每个 epoch 实现如下:
1
2
3
4
5
for x,y in dl:
pred = model(x)
loss = loss_func(pred, y)
loss.backward()
parameters -= parameters.grad * lr
首先,让我们重新初始化我们的参数:
1
2
weights = init_params((28*28,1))
bias = init_params(1)
从一个 Dataset 创建一个 DataLoader:
1
2
3
4
5
dl = DataLoader(dset, batch_size=256)
xb,yb = first(dl)
xb.shape,yb.shape
(torch.Size([256, 784]), torch.Size([256, 1]))
我们将对验证集也这样做:
1
valid_dl = DataLoader(valid_dset, batch_size=256)
让我们创建一个小批量为4进行测试:
1
2
3
4
batch = train_x[:4]
batch.shape
torch.Size([4, 784])
1
2
3
4
5
6
7
preds = linear1(batch)
preds
tensor([[-11.1002],
[ 5.9263],
[ 9.9627],
[ -8.1484]], grad_fn=<AddBackward0>)
1
2
3
4
loss = mnist_loss(preds, train_y[:4])
loss
tensor(0.5006, grad_fn=<MeanBackward0>)
现在我们可以计算梯度了:
1
2
3
4
loss.backward()
weights.grad.shape,weights.grad.mean(),bias.grad
(torch.Size([784, 1]), tensor(-0.0001), tensor([-0.0008]))
让我们把这些都放在一个函数中:
1
2
3
4
def calc_grad(xb, yb, model):
preds = model(xb)
loss = mnist_loss(preds, yb)
loss.backward()
并测试它:
1
2
3
4
calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(),bias.grad
(tensor(-0.0002), tensor([-0.0015]))
但看看如果我们调用两次会发生什么:
1
2
3
4
calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(),bias.grad
(tensor(-0.0003), tensor([-0.0023]))
梯度变了!原因是 loss.backwar 实际上将 loss 的梯度 加到当前存储的梯度中。因此,我们必须先将当前梯度设置为0:
1
2
weights.grad.zero_()
bias.grad.zero_();
注意:就地操作:PyTorch中名称以下划线结尾的方法修改其对象。例如, bias.zero_() 将张量
bias的所有元素设置为 0。
我们剩下的唯一一步是根据梯度和学习率更新权重和偏差。当我们这样做时,我们必须告诉PyTorch也不要采取这一步的梯度——否则,当我们试图在下一批计算导数时,事情会变得非常混乱!如果我们分配给张量的数据属性,那么PyTorch将不采用该步骤的梯度。以下是我们一个 epoch 的基本训练循环:
1
2
3
4
5
6
def train_epoch(model, lr, params):
for xb,yb in dl:
calc_grad(xb, yb, model)
for p in params:
p.data -= p.grad*lr
p.grad.zero_()
我们还想通过查看验证集的准确性来检查我们的情况。要决定输出是3还是7,我们只需检查它是否大于0。因此,我们可以计算我们每个样本的准确性(使用广播,所以没有循环!):
1
2
3
4
5
6
(preds>0.0).float() == train_y[:4]
tensor([[False],
[ True],
[ True],
[False]])
这给了我们计算验证准确性的函数:
1
2
3
4
def batch_accuracy(xb, yb):
preds = xb.sigmoid()
correct = (preds>0.5) == yb
return correct.float().mean()
我们可以检查它是否有效:
1
2
3
batch_accuracy(linear1(batch), train_y[:4])
tensor(0.5000)
然后将批次放在一起:
1
2
3
def validate_epoch(model):
accs = [batch_accuracy(model(xb), yb) for xb,yb in valid_dl]
return round(torch.stack(accs).mean().item(), 4)
1
2
3
validate_epoch(linear1)
0.5219
那是我们的起点。让我们训练一个epoch,看看准确性是否有所提高:
1
2
3
4
5
6
lr = 1.
params = weights,bias
train_epoch(linear1, lr, params)
validate_epoch(linear1)
0.6883
然后再做几个:
1
2
3
4
5
for i in range(20):
train_epoch(linear1, lr, params)
print(validate_epoch(linear1), end=' ')
0.8314 0.9017 0.9227 0.9349 0.9438 0.9501 0.9535 0.9564 0.9594 0.9618 0.9613 0.9638 0.9643 0.9652 0.9662 0.9677 0.9687 0.9691 0.9691 0.9696
看起来不错!我们已经创建了与准确性相似的 “像素相似度” 。我们的下一步是创建一个对象,为我们处理SGD step。在PyTorch中,它被称为优化器。
Creating an Optimizer
由于这是一个如此普遍的基础,PyTorch提供了一些有用的类,使其更容易实现。我们可以做的第一件事是用PyTorch的 nn.Linear 模块替换我们的 linear1 函数。模块是从 PyTorch nn.Module 类继承的类的对象。此类对象的行为与标准Python函数相同,因为您可以使用括号调用它们,它们将返回模型的激活。
nn.Linear 等价于我们的 init_params 和 linear 合在一起。它包含单个类中的权重和偏置。以下是我们从上一节中复制模型的方法:
1
linear_model = nn.Linear(28*28,1)
每个PyTorch模块都知道它可以训练哪些参数;它们可以通过参数方法获得:
1
2
3
4
w,b = linear_model.parameters()
w.shape,b.shape
(torch.Size([1, 784]), torch.Size([1]))
我们可以使用这些信息创建一个优化器:
1
2
3
4
5
6
7
8
class BasicOptim:
def __init__(self,params,lr): self.params,self.lr = list(params),lr
def step(self, *args, **kwargs):
for p in self.params: p.data -= p.grad.data * self.lr
def zero_grad(self, *args, **kwargs):
for p in self.params: p.grad = None
我们可以通过传递模型的参数来创建优化器:
1
opt = BasicOptim(linear_model.parameters(), lr)
我们的训练循环现在可以简化为:
1
2
3
4
5
def train_epoch(model):
for xb,yb in dl:
calc_grad(xb, yb, model)
opt.step()
opt.zero_grad()
我们的验证函数根本不需要更改:
1
2
3
validate_epoch(linear_model)
0.4157
让我们把我们的小训练循环放在一个函数中,让事情更简单:
1
2
3
4
def train_model(model, epochs):
for i in range(epochs):
train_epoch(model)
print(validate_epoch(model), end=' ')
结果与上一节相同:
1
2
3
train_model(linear_model, 20)
0.4932 0.8618 0.8203 0.9102 0.9331 0.9468 0.9555 0.9629 0.9658 0.9673 0.9687 0.9707 0.9726 0.9751 0.9761 0.9761 0.9775 0.978 0.9785 0.9785
fastai提供了 SGD 类,默认情况下,该类与我们的 BasicOptim 做相同的事情:
1
2
3
4
5
linear_model = nn.Linear(28*28,1)
opt = SGD(linear_model.parameters(), lr)
train_model(linear_model, 20)
0.4932 0.852 0.8335 0.9116 0.9326 0.9473 0.9555 0.9624 0.9648 0.9668 0.9692 0.9712 0.9731 0.9746 0.9761 0.9765 0.9775 0.978 0.9785 0.9785
fastai还提供了 Learner.fit,我们可以用它来代替 train_model。要创建 Learner,我们首先需要通过训练和验证集的 DataLoaders 来创建 DataLoaders:
1
dls = DataLoaders(dl, valid_dl)
要在不使用应用程序(如 cnn_learner )的情况下创建 Learner,我们需要传递我们在本章中创建的所有元素:DataLoaders、模型、优化函数(将把参数传递进去)、损失函数以及可选的任何要打印的指标:
1
2
learn = Learner(dls, nn.Linear(28*28,1), opt_func=SGD,
loss_func=mnist_loss, metrics=batch_accuracy)
现在我们可以调用 fit:
1
learn.fit(10, lr=lr)
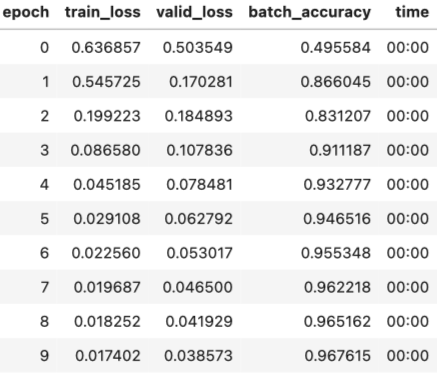
正如你所看到的,PyTorch 和 fastai 类没有什么魔力。它们只是方便的预包装件,让您的生活更轻松一点!(它们还提供了我们将在未来章节中使用的许多额外功能。)
Adding a Nonlinearity
到目前为止,我们有一个优化函数参数的一般程序,我们已经在一个非常无聊的函数上进行了尝试:一个简单的线性分类器。线性分类器在做什么方面非常有限。为了让它更复杂一点(并能够处理更多任务),我们需要在两个线性分类器之间添加一些非线性的东西——这就是我们神经网络的原因。
以下是基本神经网络的完整定义:
1
2
3
4
5
def simple_net(xb):
res = xb@w1 + b1
res = res.max(tensor(0.0))
res = res@w2 + b2
return res
就这样!我们在 simple_net 中只拥有两个线性分类器,它们之间有一个 max 函数。
在这里,w1和w2是权重张量,b1和b2是偏置张量;也就是说,最初随机初始化的参数,就像我们在上一节中所做的那样:
1
2
3
4
w1 = init_params((28*28,30))
b1 = init_params(30)
w2 = init_params((30,1))
b2 = init_params(1)
关于这一点的关键是,w1 有 30 个输出激活(这意味着 w2 必须有30个输入激活,所以它们匹配)。这意味着第一层可以构建30个不同的特征,每个特征代表一些不同的像素组合。您可以将这30更改为任何您喜欢的,以使模型或多或少复杂。
这个小函数 res.max(tensor(0.0))被称为ReLU。即用零替换每个负数。这个微小的函数也可以在PyTorch中作为 F.relu 使用:
1
plot_function(F.relu)
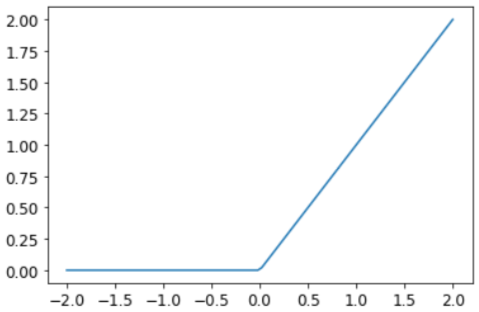
深度学习中有大量的行话,包括 rectified linear unit 等术语。正如我们在本例中看到的,绝大多数术语并不比在短代码行中实现更复杂。现实是,为了让学者们发表论文,他们需要让论文听起来尽可能令人印象深刻和复杂。他们这样做的方法之一是引入行话。不幸的是,这导致该领域最终变得比应有的更令人生畏和难以进入。你确实必须学习行话,否则论文和教程对你来说意义不大。但这并不意味着你必须发现这个术语令人生畏。请记住,当你遇到一个你以前从未见过的单词或短语时,它几乎肯定会指的是一个非常简单的概念。
基本思想是,通过使用更多的线性层,我们可以让我们的模型做更多的计算,从而建模更复杂的函数。但将一个线性层直接放在另一个线性层是没有意义的,因为当我们将事物相乘,然后将它们多次加时,这可以通过将不同事物相乘并仅相加一次来取代!也就是说,一行任意数量的线性层的一系列可以替换为具有不同参数集的单个线性层。
但是,如果我们在它们之间放置一个非线性函数,例如 max 。现在,每个线性层实际上都与其他线性层脱钩了,并且可以做自己的有用工作。max 函数特别有趣,因为它是一个简单的 if 语句。
S:从数学上讲,我们说两个线性函数的组成是另一个线性函数。因此,我们可以将任意数量的线性分类器堆叠在一起,如果没有它们之间的非线性函数,它只会与一个线性分类器相同。
令人惊讶的是,如果您能为 w1 和 w2 找到正确的参数,并且使这些矩阵足够大,可以从数学上证明,这个小函数可以任意高精度地解决任何可计算问题。对于任何任意晃动函数,我们可以将其近似为一堆连接在一起的线;为了使其更接近晃动函数,我们只需要使用更短的线。这被称为通用近似定理。我们这里的三行代码被称为 layers。第一行和第三行被称为线性层,第二行代码被称为非线性或激活函数。
与上一节一样,我们可以通过利用PyTorch将此代码替换为更简单一点的内容:
1
2
3
4
5
simple_net = nn.Sequential(
nn.Linear(28*28,30),
nn.ReLU(),
nn.Linear(30,1)
)
nn.Sequential 创建一个模块,该模块将依次调用列出的每个层或函数。
nn.ReLU 是一个PyTorch模块,其工作与 F.relu 函数完全相同。大多数可以在模型中出现的函数也具有模块相同的形式。一般来说,这只是用 nn 替换 F 并更改大写的情况。使用 nn.Sequential 时,PyTorch要求我们使用模块版本。由于模块是类,我们必须实例化它们,这就是为什么您在本示例中看到 nn.ReLU()。
由于 nn.Sequential 是一个模块,我们可以得到它的参数,它将返回它包含的所有模块的所有参数的列表。我们试试吧!由于这是一个更深层次的模型,我们将使用较低的学习率和更多的时代。
1
2
learn = Learner(dls, simple_net, opt_func=SGD,
loss_func=mnist_loss, metrics=batch_accuracy)
1
2
#hide_output
learn.fit(40, 0.1)
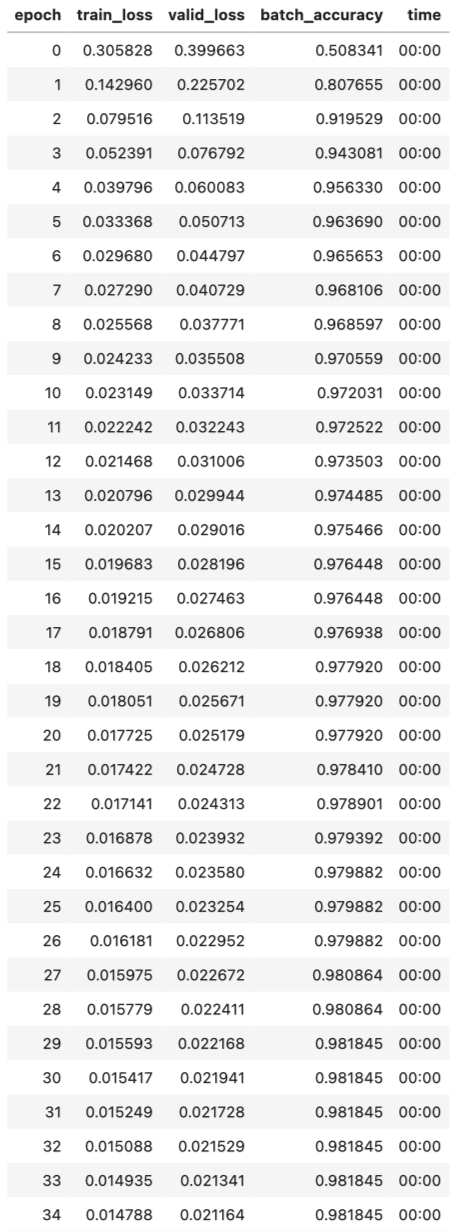
我们这里不显示40行输出来节省空间;训练过程记录在 learning.recorder 中,输出表格存储在 value 属性中,因此我们可以将训练的准确性绘制为:
1
plt.plot(L(learn.recorder.values).itemgot(2));
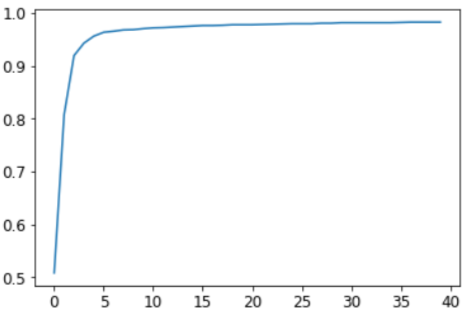
我们可以查看最终的准确性:
1
2
3
learn.recorder.values[-1][2]
0.982826292514801
在这一点上,我们有一些相当神奇的东西:
- 在给定正确参数集的情况下,可以以任何精度(神经网络)解决任何问题的函数
- 找到任何函数(随机梯度下降)最佳参数集的方法
这就是为什么深度学习可以做一些看似相当神奇的事情,比如奇妙的事情。相信这种简单技术的组合可以真正解决任何问题,这是我们发现许多学生必须采取的最大步骤之一。这似乎太好了,不可能是真的——事情肯定应该比这更困难、更复杂吗?我们的建议:试试看!我们刚刚在MNIST数据集上尝试了它,您已经看到了结果。由于我们自己从零开始做任何事情(除了计算梯度),你知道幕后没有隐藏着特殊的魔法。
Going Deeper
没有必要只停留在两个线性层。只要我们在每对线性层之间添加非线性,我们就可以添加任意数量。然而,正如您将学到的,模型越深,在实践中优化参数就越困难。在这本书的后面,您将学习一些简单但非常有效的技术来训练更深层次的模型。
我们已经知道,具有两个线性层的单个非线性就足以近似任何函数。那么,我们为什么要使用更深层次的模型呢?原因是性能。对于更深的模型(即具有更多层的模型),我们不需要使用那么多参数;事实证明,我们可以使用具有更多层的较小矩阵,并获得比使用较大矩阵和更少层更好的结果。
这意味着我们可以更快地训练模型,它占用的内存会更少。在20世纪90年代,研究人员如此专注于通用近似定理,以至于很少有人试验一个以上的非线性。这种理论上但不是实践的基础多年来一直阻碍着这个领域。然而,一些研究人员确实对深层模型进行了实验,并最终能够表明这些模型在实践中可以做得更好。最终,得出了理论结果,说明了发生这种情况的原因。今天,发现任何人使用只有一个非线性的神经网络是非常罕见的。
当我们使用相同的方法训练18层模型时会发生什么:
1
2
3
4
dls = ImageDataLoaders.from_folder(path)
learn = cnn_learner(dls, resnet18, pretrained=False,
loss_func=F.cross_entropy, metrics=accuracy)
learn.fit_one_cycle(1, 0.1)

近100%的准确性!这与我们简单的神经网络相比有很大区别。但正如您将在这本书的其余部分学到的,您只需要使用几个小技巧,才能从头开始获得如此伟大的结果。你已经知道了关键的基础部分。(当然,即使你知道了所有技巧,你几乎总是想使用PyTorch和fastai提供的预建类,因为它们让你不必自己思考所有小细节。)
-
Previous
【深度学习】GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models -
Next
【深度学习】YOLOP: You Only Look Once for Panoptic Driving Perception