Abstract

在过去的几十年里，计算光谱成像一直致力于捕捉动态世界的光谱信息。

这篇文章提出了一个可解释的神经网络的计算光谱成像。

首先，这篇文章引入了一种新的数据驱动先验，它可以自适应地利用光谱图像之间的局部和非局部相关性。

我们的数据驱动先验作为正则化集成到重构问题中。

然后，这篇文章提出将重建问题展开到一个优化启发的深度神经网络。

通过对图像相关性和系统成像模型的显式刻画，该网络结构具有较高的可解释性。

最后，通过端到端训练学习网络中的完整参数，使网络具有高空间-光谱保真度的鲁棒性能。

大量的仿真和硬件实验验证了该方法优于最先进的方法。

Introduction

光谱图像描绘出关于场景的详细场景表示，这有利于各个领域，从基础研究领域，如医疗诊断、医疗保健和遥感，到计算机视觉应用，如人脸识别、外观建模和目标跟踪。传统的光谱仪通常沿着空间维度或光谱维度扫描场景，需要多次曝光才能捕捉到全光谱图像。因此，这些系统不适合测量动态场景。

为此，研究人员开发了相当多的计算光谱成像原型。基于压缩感知(CS)理论，编码孔径快照光谱成像(CASSI)是一个很有前途的解决方案。然而，CASSI的瓶颈在于重构质量有限。光谱图像重建的核心问题是如何从欠采样的二维 measurement 中提取底层的三维光谱图像。从理论上讲，影响重构质量的有两个方面: 先验正则化和优化方法。

由于重构问题是不确定的，需要基于图像先验的正则化来划分光谱图像的结构特征。之前的方法在局部窗口内建模图像先验，如全变分(TV)，马尔可夫随机场(MRF)和稀疏性。最近提出的深度去噪先验也是一种局部先验，它逐渐处理来自局部邻近的信息。与局部先验互补，非局部先验是光谱图像重建中利用长程依赖性的替代方法。然而，现有的非局部基于先验的正则化方法，如非局部均值、协同滤波过滤和联合稀疏性等，需要手工调整参数来处理场景的各种特征。

除了先验正则化之外，优化方法也对重构质量至关重要。CASSI 的早期开发一般采用基于模型的优化技术。后来，一些工作提出学习一种从压缩图像到光谱图像之间的暴力映射。然而，这些方法忽略了系统成像模型。因此，它们在实际系统中使用时缺乏灵活性，因为不同硬件实现之间的系统成像模型在很大程度上是不同的。近年来，研究人员在自然图像CS领域发展了一些基于深度展开的优化方法。这些方法用神经网络代替了基于模型的优化中的迭代。然而，它们仍然通过显式地强制特征是稀疏的来继承局部先验。

这篇文章提出深度非局部展开，一种可解释的神经网络，用于计算光谱成像。首先，引入一种新的数据驱动先验，将优化问题规范化，以提高空间光谱保真度。数据驱动先验显式地学习了局部先验和非局部先验。通过自适应学习贡献权重，进一步研究了局部先验和非局部先验的平衡问题。然后，将正则化器纳入重构问题，并将重构问题展开到一个优化启发的深度神经网络(DNN)。通过显式地描述图像先验和系统成像模型，可以直观地解释该网络的体系结构。最后，通过端到端训练学习完整的重构网络参数，以达到高精度的鲁棒性能。

Methodology

Interpretable Unrolling-based Reconstruction

给定压缩图像 $g$ 和 sensing matrix $\Phi$，接下来的任务是估计潜在的光谱图像。

因为重构问题是严重的欠定问题，他需要解决下面的最小化问题：

$\hat f = \arg \min_f \| g - \Phi f \|^2 + \tau R(f) \tag{5}$ 其中 $R(·)$ 是正则化项，其在解上施加了一些图像先验， $\tau$ 是调节数据项和正则项的权重。上式的优化问题不能直接求解，一个通用的策略是将它分解为两个子问题。通过引入一个辅助变量，上式可以被写成一个约束优化问题：

$\hat f = \arg \min_f \|g - \Phi f\|^2 + \tau R(h) \qquad s.t \quad h = f \tag{6}$ 然后，采用 half quadratic splitting (HQS) 方法将上述优化问题转换为一个无约束优化问题：

\[(\hat f, \hat h) = \arg \min_{f, h} \|g - \Phi f\|^2 + \eta \|h - f\|^2 + \tau R(h) \tag{7}\]

其中 $\eta$ 是惩罚项。等式 $7$ 可以被拆分为两个子问题：

$\hat f^{(k + 1)} = \arg \min_f \|g - \Phi f\|^2 + \eta \| h^{(k)} - f \|^2 \tag{8}$ $\hat h^{(k + 1)} = \arg \min_h \eta \|h - f^{(k+1)}\|^2 + \tau R(h) \tag{9}$ 在这个视角， HQS 算法分为 sensing matrix $\Phi$ 和正则化 $R(·)$, 这两个子问题可以被交替求解。

这里，我们想要为等式 $8$ 中的 $f-subproblem$ 找到一个找到一个近似解。等式 $9$ 中的 $h-subproblem$ 可以使用 3.3 节中的光谱图像先验网络求解。这里我们先跳过关于 $h-subproblem$ 的细节，只给出一个通用的求解器来进行后续的推导：

\[h^{(k + 1)} = S(f^{(k + 1)}) \tag{10}\]

等式 $8$ 中的 $f-subproblem$ 是一个二次正则化最小二乘问题。

$f^{(k + 1)} = (\Phi^T \Phi + \eta I)^{-1 }(\Phi^Tg + \eta h^{(k)}) \tag{11}$ 以往图像复原领域的方法认为矩阵 $\Phi^T\Phi + \eta I$ 非常大，不能直接计算其逆矩阵。如果使用 conjugate gradient(CG) 算法，需要很多次迭代并且不能保证找到准确解。而由于图 3 所示的 sensing matrix $\Phi$ 的特殊结构，可以采用最近的方法[59, 31] 计算等式 (11) 来直接得到准确解。具体来说，给定一个 block diagonal sensing matrix $\Phi \in \mathbb{R}^{MN \times MN\Lambda}$，我们可以简单计算一个对角矩阵 $\Phi_i \Phi_i^T$：

$\Phi_i \Phi_i^T = diag\left\{\phi_1, ..., \phi_i, ..., \phi_{MN} \right\} \tag{12}$

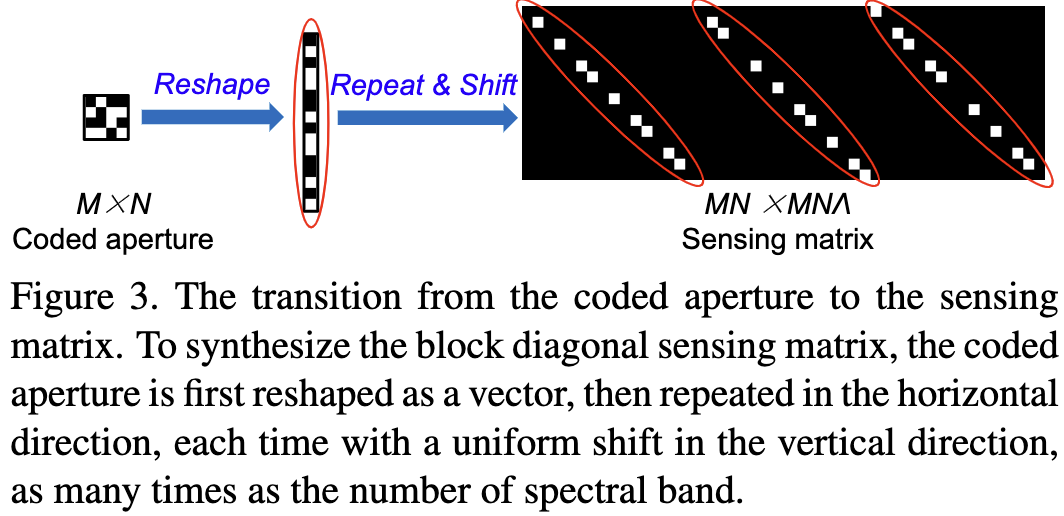
其中 $\phi_i$ 可以根据编码模板 $C$ 提前计算。通过矩阵求逆，等式 $11$ 可以被写成：

\[(\Phi^T\Phi + \eta I)^{-1} = \eta^{-1}I - \eta^{-1}\Phi^T(I + \Phi_\eta^{-1}\Phi)^{-1}\Phi\eta^{-1} \tag{13}\]

根据等式 $12$ ：

$(I + \Phi\eta^{-1}\Phi^T)^{-1} = diag\left\{\frac{\eta}{\eta + \phi_1}, ..., \frac{\eta}{\eta + \phi_i}, ..., \frac{\eta}{\eta + \phi_n}\right\} \tag{14}$ 通过插入等式 $12$, 等式 $13$ 和等式 $14$ 到等式 $11$，并且化简公式，我们有：

\[f^{(k + 1)} = h^{(k)} + \Phi^T[(g - \Phi h^{(k)})]./(\eta + \Phi\Phi^T) \tag{15}\]

在这种形式中， $f-subproblem$ 可以通过得到准确解来解决。等式 $15$ 的计算仅需线性操作，相比于基于 CG 的迭代方法有更少的计算成本。

然后我们将两个子问题通过等式 $10$ 和等式 $15$ 合并起来

\[f^{(k + 1)} = S(f^{(k)}) + \Phi^T[(g - \Phi S(f^{(k)}))]./(\eta + \Phi \Phi^T) \tag{16}\]

需要强调的是，由于计算光谱成像中 sensing matrix 的特殊结构，这是第一次推导出公式 $16$ 中的循环公式进行正则化优化。

为了求解等式 $16$，这里提出通过 DNN 展开循环，如图 4 所示。该网络由多个循环组成，每个循环包括一个光谱图像先验网络(如3.3节所介绍的)拼接上一个等式 $16$ 的线性连接。在所提出的网络中，循环以前馈的方式运行。该网络是端到端训练的，遵循图像模型，同时利用图像先验，优于以往的 separative solver。

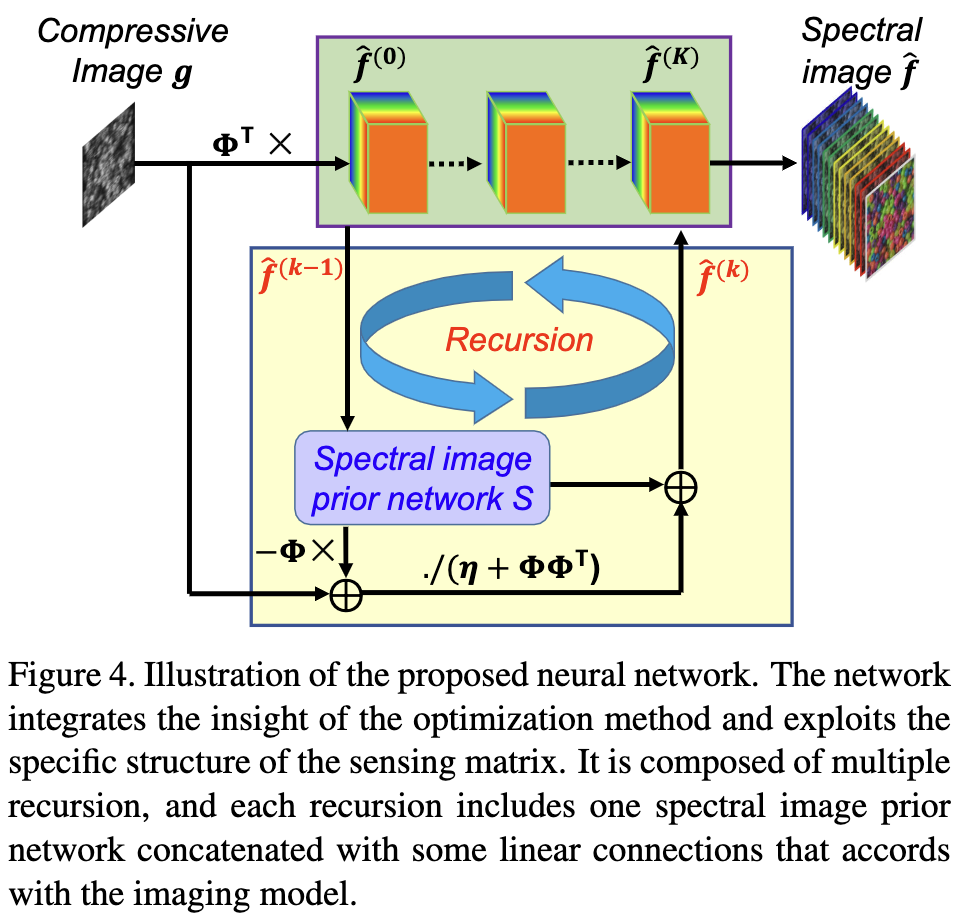
特别地，输出的压缩 patch $g$ 首先送入由 sensing matrix $\Phi^T$ 的转置参数化的线性层。输出的向量被视为初始化： $f^{(0)} = \Phi^Tg$。对于第 $k$ 次循环，输入 $f^{k-1}$ 连续被送入光谱图像先验1网络 $S(·)$ 和一个残差网络块。在残差网络块中，恒等连接和残差连接分别模拟等式 $16$ 的第一部分和第二部分。在残差连接中，输入被送入一个由 $\Phi$ 参数化的线性层，加上压缩图像 $g$, 然后是由 $\eta + \Phi \Phi^T$ 和 $\Phi^T$ 参数化的线性连接。这样的循环进行 $K$ 次。

Neural Local and Non-local Priors

Conclusion

这篇文章提出了一个可解释的神经网络的计算光谱成像。

该方法综合了 deep unrolling 和NLS 的优点:

1) 通过利用 sensing matrix 的块对角特性，推导出一种新的递归公式，在此基础上，开发了一个可解释的神经网络来解决计算光谱成像中的重建问题。

2）通过认识到以往的深度学习方法仅通过局部卷积来考虑局部先验，这篇文章提出了一种自适应地将非局部先验纳入光谱图像先验网络的机制。

该方法无需优化参数调整，降低了计算复杂度。

在实际硬件样机上验证了该方法的有效性。

未来的一个研究方向是将所提出的方法扩展到更多的光谱图像处理问题，如光谱插值和去马赛克。

另一个方向是加速该方法实现视频速率重构，从而实现高光谱视频的实时采集。

Summary

重构问题需要解决以下最小化问题：

\[\hat x = \mathop{\text{argmin}}_x \|y - \Phi x\|^2 + \tau R(x) \tag{1}\]

等式 $(1)$ 可以通过引入辅助变量写成一个带约束的优化问题：

$\hat x = \mathop{\text{argmin}}_x \|y - \Phi x\|^2 + \tau R(z) \quad s.t. \quad z = x \tag{2}$ 然后采用 half quadratic splitting (HQS) 方法将上述约束优化问题转换为无约束优化问题：

$(\hat x, \hat z) = \mathop{\text{argmin}}_{x, z} \|y - \Phi x\|^2 + \eta \|z - x\|^2 + \tau R(z) \tag{3}$ $\eta$ 是惩罚项，等式 $(3)$ 可以拆分为两个子问题 $x-$subproblem 和 $z-$subproblem：

\[\hat x^{(k + 1)} = \mathop{\text{argmin}}_x \|y - \Phi x\|^2 + \eta \|z^{(k)} - x\|^2 \tag{4}\] \[\hat z^{(k + 1)} = \mathop{\text{argmin}}_z \eta\| z - x^{(k + 1)} \|^2 + \tau R(z) \tag{5}\]

等式 $(4)$ 中的 $x-$subproblem 是一个 quadratic regularized least-squares 问题。一个 closed form 为：

\[x^{(k + 1)} = (\Phi^\top \Phi + \eta I)^{-1} (\Phi^\top y + \eta z^{(k)}) \tag{6}\]

给定一个 block diagonal sensing matrix $\Phi \in \mathbb{R}^{MN \times NM\Lambda}$:

\[\Phi_i \Phi_i^\top = \text{diag}\{\phi_1, ..., \phi_{MN}\} \tag{7}\]

其中 $\phi_i$ 可以根据 code aperture pattern $C$ 提前计算出来。通过矩阵求逆法则：

\[(\Phi^\top \Phi + \eta I)^{-1} = \eta^{-1}I - \eta^{-1} \Phi^\top (I + \Phi \eta^{-1} \Phi^\top)^{-1} \Phi \eta^{-1} \tag{8}\]

根据等式 $(7)$：

\[(I + \Phi \eta^{-1} \Phi^\top)^{-1} = \text{diag}\{\frac{\eta}{\eta+ \phi_1}, ..., \frac{\eta}{\eta + \phi_n}\} \tag{9}\]

通过将等式 $(7), (8), (9)$ 插入等式 $(6)$，并且简化公式，得到：

$x^{(k + 1)} = z^{(k)} + \Phi^\top [(y - \Phi z^{(k)})./(\eta + \Phi \Phi^\top)]$ 以这种方式， $f-$subproblem 可以求解得到精确解。

【深度学习】DNU: Deep Non-local Unrolling for Computational Spectral Imaging