Abstract

编码孔径快照光谱成像(CASSI)系统将三维高光谱图像编码到单个二维压缩图像中，然后采用逆优化算法重建潜在的高光谱图像，这种方法具有快照的明显优势，但通常重建精度较低。

为了提高精度，现有的方法要么尝试设计替代的编码孔径，要么尝试设计先进的重构方法，但无法通过统一的框架将两者联系起来，限制了精度的提高。

这篇文章提出了一种基于卷积神经网络的端到端方法，通过联合优化编码孔径和重构方法来提高精度。

一方面，基于CASSI前向模型的特点，设计了一种重复模式的编码孔径，其实体作为网络权值来学习。

另一方面，通过同时利用HSI内部的固有属性，以及跨空间和光谱维度的广泛相关性来进行重建。

通过利用深度学习的力量，编码孔径设计和图像重建通过一个统一的框架连接和优化。

Introduction

高光谱成像系统密集采样场景中每个点的光谱信号。 捕获的高光谱图像提供场景大量的光和材料信息，其有利于各种各样的领域，包括遥感， 计算机视觉， 医疗诊断。 现有的 2D 成像传感器无法通过单次曝光捕获3D HSI。 进而，传统的高光谱成像系统[7]-[10]牺牲了时间维度，并沿着空间或光谱维度扫描场景，以捕获完整的HSI。因此，这些基于扫描的系统不能用于捕获动态场景。

由于重建是一个严重的病态问题，重建数据的准确性通常有限。为了提高 CASSI 系统的准确性，现有方法主要从两个阶段进行，即观测阶段和重建阶段。从观测阶段开始，设计了替代编码孔径模式，目的是更有效地编码 HSI 信息。从重建阶段开始，随着CS理论的推进，提出了复杂的重建算法[19]，[20]。这两个阶段通常共同决定重建的准确性。然而，现有的方法忽略了这两个阶段之间的联系，通常每次只考虑一个阶段，这限制了准确性的提高。

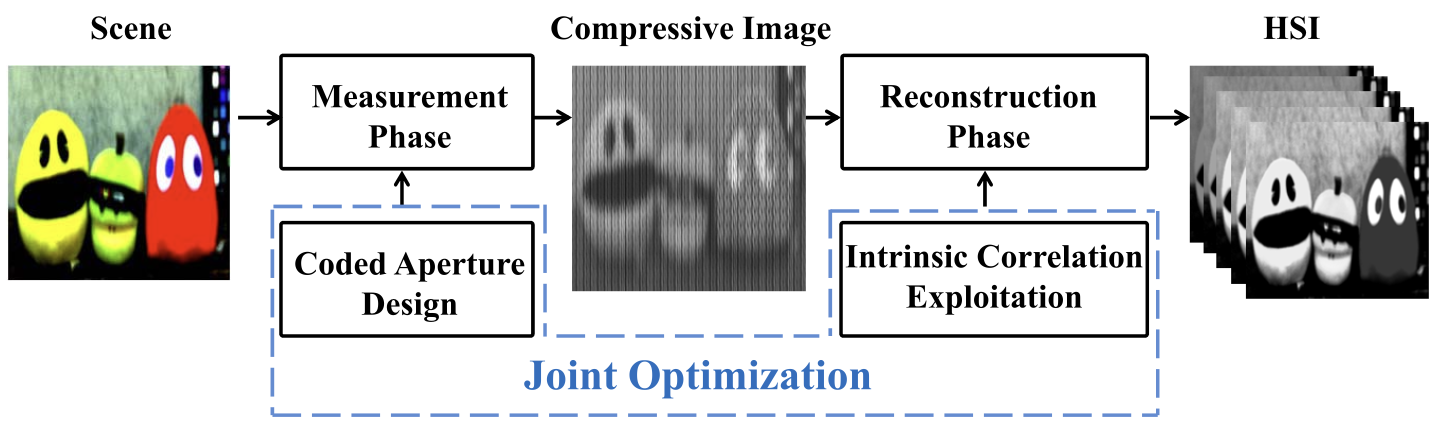
在本文中，我们提出了一种基于卷积神经网络工作（CNN）的端到端方法，该方法共同优化了编码孔径和图像重建（图1）。具体来说，对于观测阶段，根据 CASSI 正向模型的性质，我们将 CASSI 正向模型从基于图像的建模分解为基于 patch 的建模，这与CNN的复杂性要求保持一致。这种动机来自一个关键观察，即二维压缩图像的每个小 patch 都对应于潜在 3D HSI 中的 oblique parallelepiped[21]。通过充分利用基于 patch 的建模的优点，我们进一步设计了循环的编码孔径模式，并通过将其视为网络权重来优化编码模板。然后，对于重建阶段，鉴于空间和光谱维度的相关性，我们设计了一个空间网络和一个光谱网络，以利用HSI的内在属性，并连接这两个网络以完成重建。通过利用深度学习的力量，编码孔径优化和HSI重建被统一到一个框架中，称为HyperReconNet。据我们所知，这是第一次将CNN与压缩高光谱成像系统集成，直接从2D压缩图像中重建3D HSI。此外，这是第一次尝试连接观测阶段和重建阶段之间的联系，这提高了重建的保真度，并为使压缩高光谱成像系统实用性向前迈出了坚实的一步。

本文的其余部分组织如下。第二节回顾了相关工作。第三节介绍了提出的方法。实验结果见第四节。第五节得出结论并讨论未来方向。

Related Work

Optimal Coded Aperture Design

根据CS理论，将 HSI 映射到 CASSI 中压缩图像的感知矩阵在重建质量中起着至关重要的作用。使用固定探测器和色散棱镜，感知矩阵仅由编码孔径的实体决定。编码模板的初始采用随机二值设计。然而，随机编码孔径没有充分利用 CASSI 感知机制的结构，这导致了次优重建。为了使 CASSI 观测包含更多有用的信息，近年来，编码孔径模式的优化引起了越来越多的关注[17]。Arguello 开始从对投影矩阵的限制等距属性（RIP）[37]的分析中优化编码孔径，该矩阵是具有特定基矩阵的传感矩阵的乘积[38]，[39]。它提出将编码模板优化问题转换为秩最小化问题，该问题已用通用算法解决。这种方法侧重于光谱选择性，这需要多个镜头，因为对来自不同镜头的多次观测进行了操作，以获得包含且仅包含所需光谱带信息的新观测。最近，微光刻和涂层技术的新进展允许设计彩色编码孔径，这也被引入CASSI系统[40]，[41]。Parada-Mayorga转而分析投影矩阵的一致性，而不是RIP[18]。有人提出，彩色编码孔径模式的优化等同于相干性最小问题。Ramirez和Arguello提出对投影矩阵的Gram矩阵的实体分布进行建模。彩色编码孔径的设计使克矩阵的方差最小化[42]-[44]。对于这些方法，它应该在优化开始之前确定一个特定的稀疏矩阵。这些方法可以根据场景特征自适应地学习稀疏性基础。从这个意义上说，在成像之前没有稀疏性基础，因此不能用于设计编码孔径。

在上述编码孔径优化方法趋势的推动下，本文通过数据驱动方法解决问题，该方法与之前基于优化的方法相辅相成。我们认为，基于优化和数据驱动的编码孔径设计方法是编码孔径成像成功的两个互补方向。

Joint Coded Apeture Optimization and HSI Reconstruction

HSI Reconstruction

受基于学习的图像恢复[54]-[56]令人印象深刻的发展的启发，我们建议通过CNN进行HSI重建。鉴于HSI的3D性质，训练特定网络需要高计算资源。因此，很难在网络内支持完整的图像吞吐量。为此，我们建议采用分而治之策略，并每次重建小的 3D HSI patch[19]，[20]，[29]。

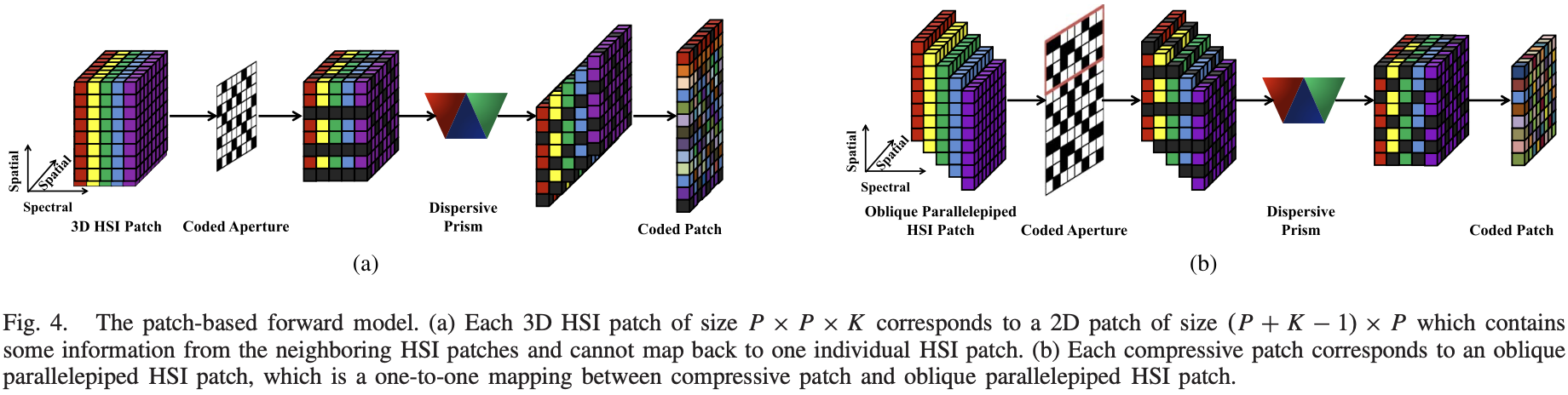
现在，瓶颈在于如何将基于图像的重建划分为基于 patch 的重建。直观上，我们可以通过系统正向模型跟踪一个大小为 $P \times P \times K (P<M，P<N)$ 的 3D HSI patch ，如图 4a 所示。在HSI patch 被编码模板调制并由棱镜色散后，探测器上的相应测量是尺寸 $(P+K-1) \times P$ 的二维 patch。然而，2D patch 将包含来自相邻 HSI patch 的场景信息，并且不能映射到单个HSI patch。因此，图4a 中的分解方法无法满足要求。

根据 CASSI 正向模型的性质，我们通过光学系统在探测器上追踪 $P \times P$ 补丁，如图4b [21]所示。我们可以看到，相应的 HSI patch 不再是一个立方体，而是一个具有 $K$ 位移光谱带的 oblique parallelepiped。 每个波段相对于其相邻波段在色散方向上有一个像素的偏移。图 4b 中的分解方法提供了一种在 oblique parallelepiped HSI patch 和探测器上的二维压缩 patch 之间的一对一映射，从而有效地符合分而治之策略。

Coded Aperture Optimization

从Sec III-B 的分析，我们可以在3D oblique parallelepiped HSI patch 和 2D 压缩 patch 之间获得一对一的映射。一对一映射允许我们将图像重建分解为小规模问题。然而，对于 图4b 中的正向模型，具有 $P \times P$ 空间点和 $K$ 光谱带的小型 oblique parallelepiped HSI patch 由尺寸 $(P + K − 1）\times P$ 的编码孔径 patch 进行空间调制。很明显，编码孔径 patch 的空间分辨率大于 oblique parallelepiped。因此，编码模板 patch 不仅调制当前 oblique parallelepiped 补丁，还调制其相邻的 patch。也就是说，与相邻的 oblique parallelepiped patches 相对应的编码模板 patches 将具有重叠区域。从这个意义上说，如果我们为当前 oblique parallelepiped HSI patch 优化编码模板 patch，我们必须考虑它对相邻 patch 的影响。这种串扰将遍布整个图像，因此一对一映射是无效的。

为了消除编码模板的串扰效应，我们建议设计一个局部随机和全局重复编码孔径。在这个设计中，$P \times P$ 实体被视为基本单位。一旦优化，基本单元将拼贴到全分辨率，作为最终编码编码模板。通过这种方式，对于大小为 $(P + K − 1) \times P$ 的每个编码模板 patch，上部 $(K − 1) \times P$ 实体（如图4b中编码孔径的红色框所示）与下部 $(K −1) \times P$ 实体相同。

具体来说，编码模板的基本单位表示为：

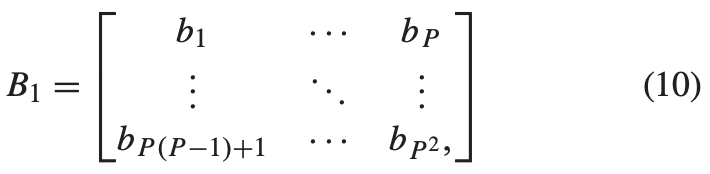
其中 $B_1$ 中的元素需要学习， 例如 $b_p = 1$ 或者 $0$ ($p = 1, …, P^2$)。由于信息由棱镜光谱色散，因此对应于每个光谱带的编码孔径相对于其相邻带具有一像素的偏移。因此，第k个光谱带的二值编码模板可以描述为 $B_1$ 的循环位移，即:

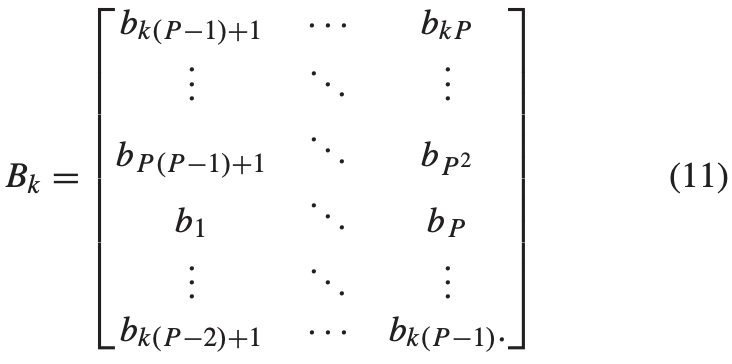
例如，图6显示了三个相邻波段的编码模板。

为了将这种结构转换为神经网络并学习最佳编码模板，我们首先将 oblique parallelepiped patch $s^i$ 的下部移动到图7中橙色线所示的上部位置，然后得到一个立方HSI patch $\hat s^i_p$。我们在 $\hat s^i$ 中提取空间位置 $p(p = 1，···，P^2)$ 的所有光谱元素，表示为 $\hat s^i_p \in R^K$ 。令 $\hat s^i_{p,k}(k = 1,···，K)$ 表示 $\hat s^i_p$ 中的第 $k$ 个光谱元素。我们将 $b_p$ 设置为 $1 \times 1$ 权重，并获得编码的 3D patch。

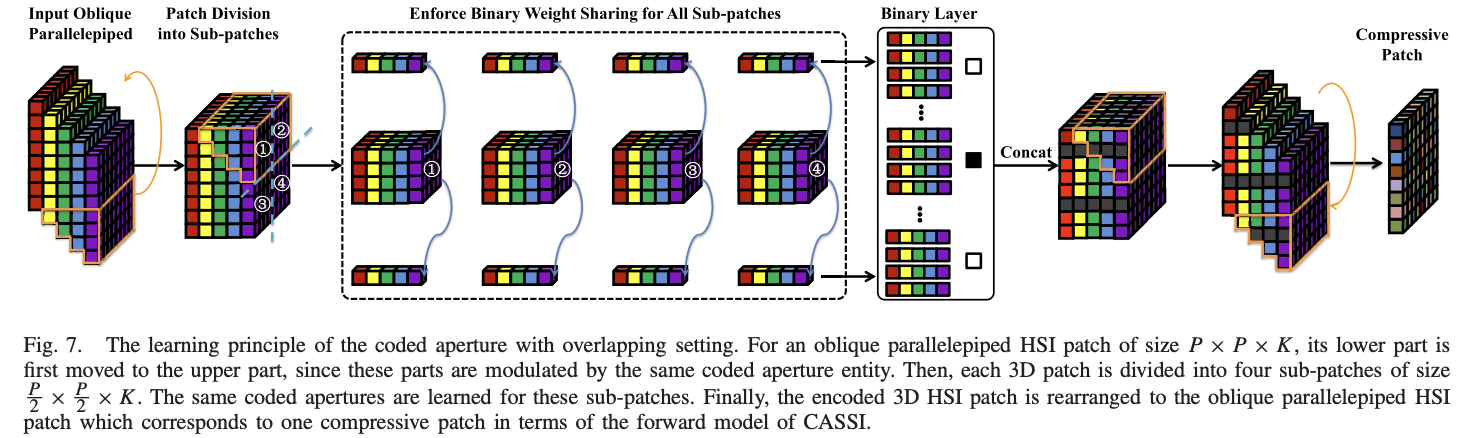
然后，通过返回橙色线所示的移动部分，我们得到了编码的 oblique parallelepiped。到目前为止，空间调制模型是为基于 CNN 的编码模板优化而构建的。然后，通过以下光谱色散和求和，我们获得了二维压缩测量。

BinaryConnect方法[59]用于通过符号函数将 $B_1$ 中的元素学习为 0 或 1，即，

$b^r$ 是 $B_1$ 的实值元素。 来自于 coding CNN 学习到的 $b^b$ 是 $B_1$的值并且建立了最优编码模板。通过重复这种学习元素来获得完整的编码模板，以适应编码模板的空间分辨率。可以在采用 DMD 或 LCoS 的现有系统上轻松实现这种编码模板。

由于学习的编码模板均匀地用于每个 oblique parallelepiped HSI patch，因此相应的重建 patch 是非重叠的。 因此，很容易引入 blocky artifacts。为了减轻 blocky artifacts 并提高重建质量，我们提出了重叠处理。通过这种方式，每个 oblique parallelepiped patch 被划分为四个大小为 $\frac{P}{2} \times \frac{P}{2} \times K$ 的 patch， 其共享编码模板。因此对于 $B_1$ 中ed编码模板，需要学习 $\frac{P^2}{4}$ 而不是 $P^2$ 个值。 这种处理可以使大小为 $P \times P \times K$ 的重建的 oblique parallelepiped patch 具有大小 $\frac{P}{2} \times \frac{P}{2}$ 与其相邻 patch 的空间重叠。因此，重建的完整 HSI 可以通过融合所有 patches 和 平均重叠区域得到。以 $P = 8$ 为例，如图7 所示，它可以分为四个尺寸为 $4 \times 4 \times K$ 的 sub-patches。因此，只需要估计16个二值，每个二值对应四个不同的输入。例如，$\hat e(s_1^i), \hat e(s_5^i), \hat e(s_{33}^i), \hat e(s_{37}^i)$ 共享等式 12 中的参数 $b_1$。

Conclusion and Discussion

这篇文章尝试引入带有CASSI的CNN，它可以同时优化编码孔径和重构HSI。从观测阶段开始，根据 CASSI 前向模型的性质，将编码孔径实体作为网络权值进行优化。从重建阶段开始，设计了两个子网络，以充分利用跨空间和光谱维度的相关性。通过利用深度学习的力量，编码孔径优化和HSI重建连接到一个统一的框架。

有几个问题需要进一步努力。第一个方向来自于这篇文章的动机，试图在编码孔径优化方法和HSI重建算法之间架起桥梁。这篇文章在深度学习的框架下，建立了编码孔径与重构算法之间的隐式连接。然而，与压缩感知背后丰富的理论相比，这种联系似乎有些野蛮，缺乏完整的数学解释。现在由 HyperReconNet 优化得到的编码模板与之前基于凸和非凸优化方法并不 compatible。例如，表VI显示了在 Harvard 数据集上的 TwIST 和 3DNSR 全局随机和最优编码模板的比较。编码孔径优化后的重构质量较全局随机编码孔径差，说明编码孔径应与重构算法同时优化。我们还需要进一步努力，以本文的线索深入研究，在理论支持下建立明确的模型。此外， 这篇文章提出的方法是互补的而不是替代的， 之前的方法基于凸和非凸优化。

第二个方向指向网络本身。这篇文章论证了用CASSI引入CNN的可能性。由于训练复杂度高的缺点，必须采用分治策略，这可能会导致次优结果。需要进一步努力简化网络架构，以适应全分辨率图像训练。由于测试复杂度低的优势，需要在实际系统的平台上做大量的工作。将该方法部署到便携式计算设备(如FPGA)中并非易事。进一步将便携式计算设备与光学硬件系统相结合，将加快压缩高光谱成像仪向实际应用的更新。

该方法的主要局限性来自于训练和测试之间的数据不匹配的困境，这一问题存在于图像处理和计算机视觉领域的所有基于训练的方法中。作为参考，进行了交叉验证实验，在不同的数据集上进行训练和测试。结果见表七。可以看出，在交叉验证过程中，性能急剧下降。这主要是由于两组数据所使用的高光谱相机时代完全不同，包括制造商、相机型号、光谱范围和成像方式，因此两组数据的图像属性是异质性的.我们仍然希望寻求更稳健的方法，以处理相机配置的多样性。

• Previous
  【深度学习】Language Models Can See: Plugging Visual Controls in Text Generation
• Next
  【深度学习】Hyperspectral Image Reconstruction Using a Deep Spatial-Spectral Prior