Abstract

为了解决编码孔径快照光谱成像(CASSI)的反问题，即从二维 compressed measurement 中重构三维高光谱图像(HSIs)，已经开发了许多算法。

近年来，基于学习的方法表现出了良好的性能，并主导了主流研究方向。

然而，现有的基于 CNN 的方法在捕获远程依赖和非局部自相似性方面存在局限性。

以前基于 Transformer 的方法密集采样 token，其中一些 token 没有信息，并计算一些内容不相关的标记之间的多头自注意力(MSA)。

这并不符合HSI信号的空间稀疏特性，并限制了模型的 scalability。

这篇文章提出了一种新的基于 Transformer 的 coarse-to-fine sparse Transformer(CST) 方法，首先将HSI sparsity 嵌入深度学习中进行 HSI 重构。

特别地，CST使用提出的spectral-aware screening mechanism(SASM)进行 coarse patch selecting。

然后，将所选择的 patch 输入到定制的 spectra-aggregation hashing multi-head self-attention(SAH-MSA)中，进行fine pixel clustering 和自相似性捕获。

Introduction

这项工作的主要贡献可以概括如下：

这篇文章提出了一种新的基于 Transformer 的方法，CST，用于HSI重建。据我们所知，这是第一次尝试将HSI空间稀疏性嵌入到基于学习的算法中。
这篇文章提出了用HSI信号定位有信息区域的SASM。
定制了 SAH-MSA 来捕获密切相关模式的交互。
在仿真的所有场景中，CST算法的计算复杂度都大大低于SOTA算法。此外，在真实的HSI恢复中， CST比现有的方法获得了更令人满意的视觉效果。

Method

图3中的CST由两个关键成分组成： spectra-aware screening mechanism(SASM) 用于 coarse patch selecting 和 spetra-aggregation hashing multi-head self-attention 用于 fine pixel clustering。图3(a) 描述了 SASM 和 CST 的网络架构。 Fig.3(c) 解释了 SAH-MSA，这是 SAHAB 最重要的成分。

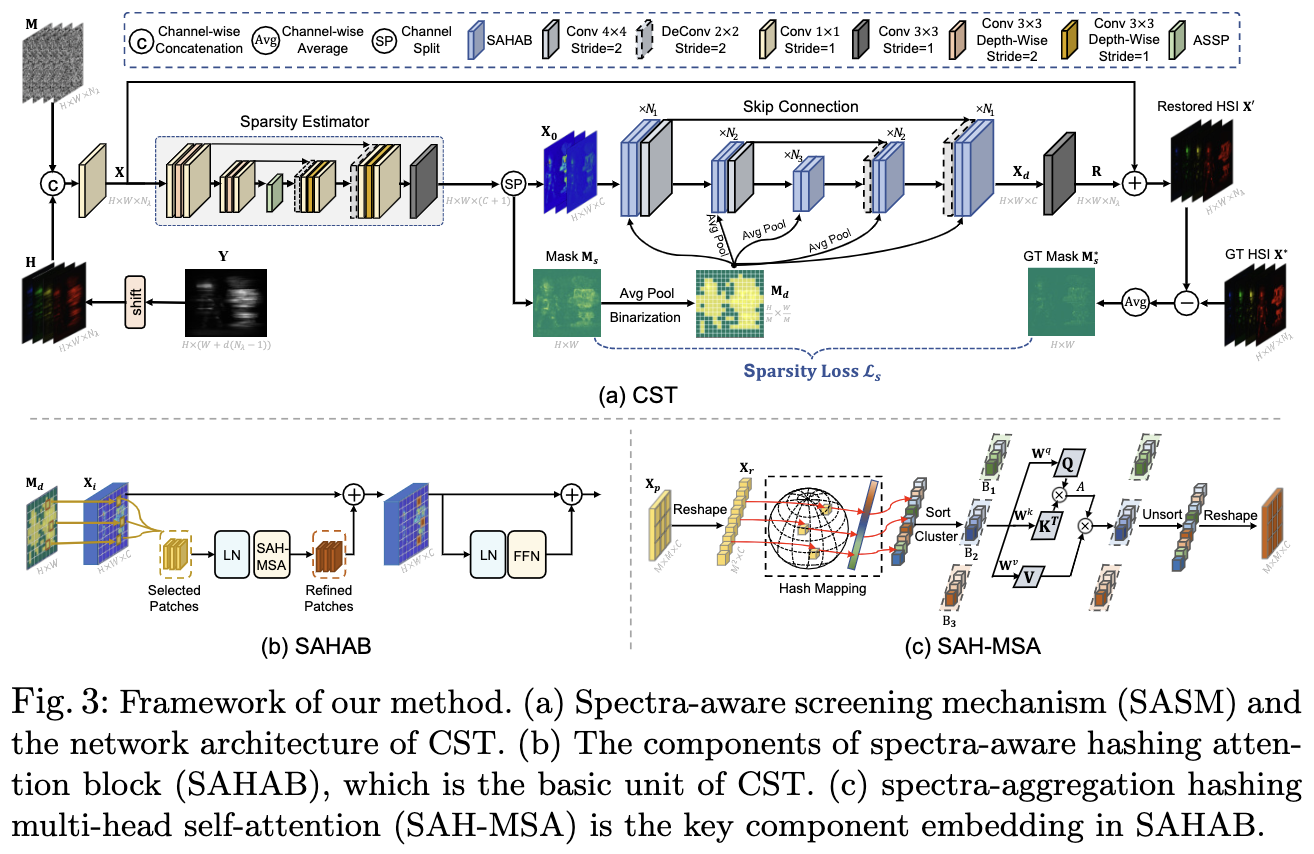
Network Architecture

首先，一个 sparsity estimator 将 X 处理为一个 sparsity mask $M_s \in \mathbb{R}^{H \times W}$ 和浅层特征 $X_0 \in \mathbb{R}^{H, W, C}$。

其次，浅层特征 $X_0$ 通过三阶段对称的编码器-解码器结构，得到深层特征 $X_d \in \mathbb{R}^{H \times W \times C}$。

编码器或解码器的第 i 个阶段包含 $N_i$ 个 SAHABs。如图3(b)， SAHAB 由两个 layer normalization(LN)，一个 SAH-MSA，和一个 FFN 组成。

对于降采样分别使用 strided conv4x4 和 deconv 2x2 层。

最后，对 $X_d$ 应用一个 conv3x3 产生 residual HSIs $R \in \mathbb{R}^{H \times W \times N_\lambda}$。

然后重构的 HSIs $X’$ 可以通过 $R$ 和 $X$ 的和得到。

Spectra-Aware Screening Mechanism

HSI信号在空间维度上表现出高度的稀疏性。然而，原始的全局Transformer对特征映射中的所有 token 进行采样，而基于窗口的本地Transformer 对每个非重叠窗口中的所有 token 进行采样。这些 Transformer 在计算MSA时选取了很多信息不足的区域，降低了模型的效率。为了解决这一问题提出了SASM方法用于 coarse patch selecting，即筛选HSI信息密集的区域来产生 Token。这节将分三部分介绍SASM，分别是稀疏估计器、稀疏损失和patch选择

Sparsity Estimator：在这一部分详细介绍了第4节中提到的稀疏性估计。如图3 (a)所示，稀疏性估计器采用u型结构，包括两级编码器、ASSP模块和两阶段解码器。编码器的每一阶段由两个 conv1x1 和一个 strided depthwise conv3x3 组成。解码器的每一阶段包含一个 strided deconv2x2，两个 conv1x1和一个 depthwise conv3x3。sparsity estimator 将初始化特征 $X$ 作为输入，产生浅层特征 $X_0$ 和稀疏 mask $M_s$。通过最小化所提出的稀疏性损失来实现这一点。

Sparsity Loss：为了监督 $M_s$，我们需要一个参考，可以告诉在 HSI 上空间稀疏的HSI信息在哪里。由于背景较暗且信息不足，HSI表征的区域大致等价于难以重构的区域。因此，通过平均重构 HSI $X’$ 和 ground truth $X^$ 之间的差值在光谱维度上取平均设计参考信号 $M_s^ \in \mathbb{R}^{H \times W}$。

\[M^*_s = \frac{1}{N_\lambda} \sum_{n_\lambda = 1}^{N_\lambda} \left| X'(:, :, n_\lambda) - X^*(:, :, n_\lambda)\right|\]

然后， $L_s$ 通过计算预测的 sparsity mask $M_s$ 和参考 sparsity mask $M_s^*$ 的均方根误差构建

$L_s = \| M_s - M_s^* \|_2$ 通过最小化最小二乘，利用稀疏性估计器检测前景中难以重构的区域。此外，整体训练目标 $L$ 为 $L_s$ 与 $L_2$ 损失的加权和：

\[L = L_2 + \lambda · L_s = \|X' - X^*\|_2 + \lambda · \| M_s - M_s^*\|_2\]

Patch Selection： SASM将特征映射划分为大小为 $M \times M$ 的不重叠 patches。然后利用预测的 sparsity mask 筛选出具有HSI表示的patch，并送入SAH-MSA，如图3 (b)所示。具体来说， $M_s$ 通过平均池化被降采样，然后被二值化为 $M_d \in \mathbb{R}^{\frac{H}{M} \times \frac{W}{M}}$ 。我们使用超参数稀疏比 $\sigma$ 来控制二值化。更具体地说，选择下采样稀疏 mask 上值最高的 k 个patch。$k$ 由 $\sigma$ 控制： $k = \lfloor (1 - \sigma) \frac{HW}{M^2} \rfloor$。 $M_d$ 上每个像素对应特征图上 $M \times M$ patch, 并且它的 0-1 值分类这个 patch 是否被筛选出。然后将 $M_d$ 应用于每个 SAHAB 的 SAH-MSA。当 $M_d$ 被用于第 i 个阶段时(i > 1)，一个平均池化操作用来降采样 $M_d$，使其匹配第 i 个阶段特征图的空间分辨率。

Spectra-Aggregation Hashing Multi-head Self-Attention.

之前的 Transformer 计算所有采样 token 之间的MSA，其中一些甚至在内容上不相关。这可能会导致计算效率低下，降低模型的效益，并容易阻碍收敛。稀疏编码方法假设图像信号可以被表示为在字典信号上的一种稀疏线性组合。受此启发，提出了 SAH-MSA 用于 fine pixel clustering。SAH-MSA增强了MSA机制的稀疏性约束。特别是，SAH-MSA只计算内容中密切相关的 token 之间的自注意力，这解决了以前transformer 的限制。

SAH-MSA通过搜索产生最大内积的元素来学习将 token 聚集到不同的桶中。如图 3(c) 所示，将 patch T恩正图表示为 $X_p \in \mathbb{R}^{M \times M \times C}$，其通过 sparsity mask 筛选出。将 $X_p$ reshape 为 $X_r \in \mathbb{R}^{N \times C}$, 其中 $N = M \times M$ 是元素的数量。随后，我们使用哈希函数在光谱上聚合信息，并将 C-Dimension 元素(pixel vector) $x \in \mathbb{R}^C$ 映射为一个整数哈希码。

Experiment

Qualitative Results

Simulation HSI Restoration. 图4比较了 CST-L 和 7个 SOTA 算法复原的仿真 HSI 在场景2上的 28 通道的 4 个。请放大以便更好地显示。从重构的HSI(右)和黄框中放大的 patch 可以观察到，CST可以有效地产生感知愉快的图像，具有更生动的尖锐边缘细节，同时在不引入伪影的情况下保持均匀区域的空间平滑。相比之下，其他方法无法恢复细粒度的详细信息。它们要么获得过度光滑的结果，牺牲结构内容和高频细节，要么产生斑点纹理和彩色伪影。图4给出了RGB图像中绿色方框所选区域(左上)对应的光谱密度曲线(左下)。CST 的曲线与真实值具有最高的相关系数。这一证据清楚地证明了CST的光谱维一致性重建的有效性。

Real HSI Restoration. 作者在真实HSI重建中评估CST。与之前的工作一致，在 KAIST 和 CAVE 数据集上重新训练了 CST-L。为了模拟真实的CASSI，在训练过程中，在 measurement 中注入了 11-bit 的shot噪声。重建的HSI比较如图6所示。CST-L在细节恢复和真实噪声去除方面具有显著优势。这些结果验证了该方法的鲁棒性、可靠性和泛化能力。

Conclusion

这篇文章研究了 HSI 重构中的一个关键问题，即如何将 HSI 稀疏性嵌入到基于学习的算法中。

为此，这篇文章提出了一种新的基于 Transformer 的 HSI 恢复方法，命名为 CST。

CST 首先利用 SASM 检测具有HSI 表征的 informative 区域。

然后将检测到的 patch 输入到定制的 SAH-MSA 中，对内容密切相关的空间分散 token 进行聚类，计算MSA。

这种从粗到精的学习模式使 CST 能够更好地感知空间稀疏的 HSI 信息，减少了对 dark uninformative 区域的低效计算，从而提高了模型的成本效益。

大量的定量和定性实验表明，CST显著优于其他SOTA方法，同时需要更低的计算成本。

此外，在真实的HSI重建中，与现有的算法相比，CST产生了更有视觉效果的结果，具有更细粒度的细节和结构内容。

【深度学习】CST：Coarse-to-Fine Sparse Transformer for Hyperspectral Image Reconstruction