Introduction

最近，GANs和VAEs这两个重要的生成模型已经获得了很多成功和认可。GANs在多个应用程序中都能很好地工作，然而，它们很难训练，由于一些挑战，比如模式坍塌和梯度消失，它们的输出缺乏多样性。然而，虽然 VAEs 具有坚实的理论基础，但是建立一个良好的损失函数模型是 VAEs 系统的一个挑战。

还有一组技术从物理现象中获得灵感，其基于概率似然估计方法, 叫做扩散模型。扩散模型背后的中心思想来自气体分子热力学，其中分子从高密度扩散到低密度区域。在物理学文献中，这种运动通常被称为熵或 heat death 的增加。在信息论中，这等同于噪音的逐渐干扰导致的信息丢失。

扩散模型的关键概念是，如果我们可以建立一个学习模型，学习信息由于噪声造成的系统衰减，那么应该可以逆转这个过程，从而从噪声中恢复信息。这个概念与 VAE 相似，它试图通过首先将数据投影到隐空间，然后将其恢复到初始状态来优化目标函数。然而，该系统不是学习数据分布，而是旨在模拟马尔可夫链中的一系列噪声分布，并通过以分层方式对数据去噪来“解码”数据。

Denoising Diffusion Model

去噪扩散模型的想法已经存在了很长时间。它起源于扩散映射概念，这是机器学习文献中使用的维度还原技术之一。它还借鉴了在许多应用中使用的马尔可夫链等概率方法中的概念。

去噪扩散建模是一个两步过程：正向扩散过程和反向重建过程。在正向扩散过程中，逐步引入高斯噪声，直到数据变成所有噪声。反向重建过程通过使用神经网络模型学习条件概率密度来消除噪声。这样一个过程的示例可以可视化为下图：

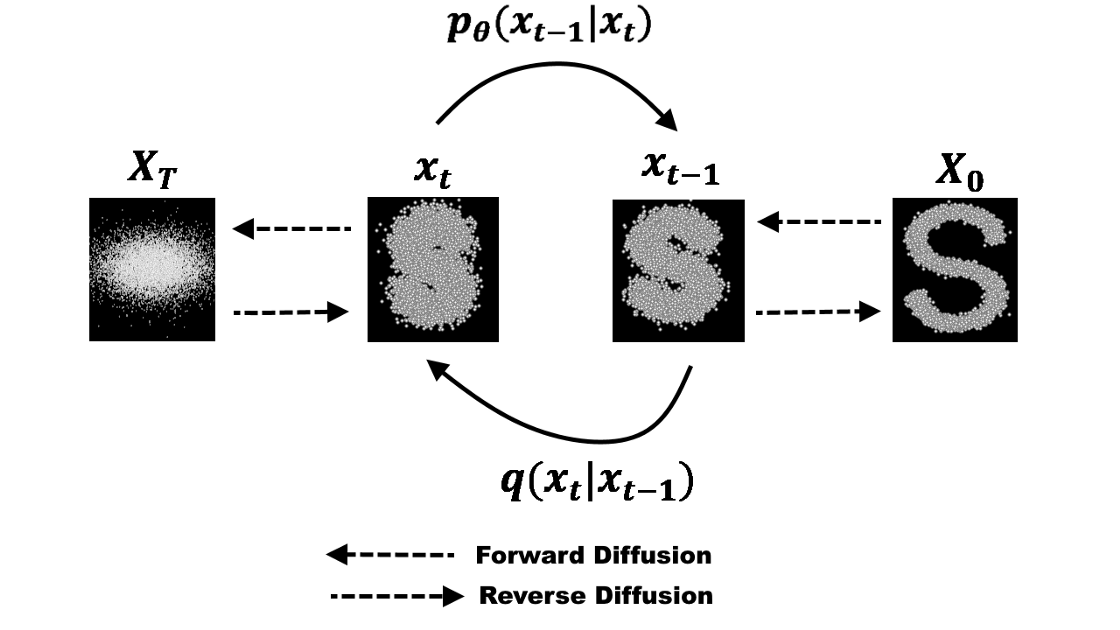
Forward Process

我们可以将正向扩散过程定义为马尔可夫链，因此，与VAE中的编码器不同，它不需要训练。从初始数据点开始，我们为连续 $T$ 步添加高斯噪声，并获得一组噪声样本。时间 $t$ 的概率密度预测仅取决于时间步 $t-1$ 的直接前身，因此，条件概率密度可以计算如下：

\[q(x_t \mid x_{t-1}) = N(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_tI)\]

然后，整个过程的完整分布可以计算如下：

\[q(x_{0:T} \mid x_0) = q(x_0) \prod_{t=1}^T q(x_t \mid x_{t-1})\]

在这里，密度函数的平均值和方差取决于参数 $\beta_t$，这是一个超参数，其值可以在整个过程中视为常数，也可以在连续的时间步中逐步更改。

为了使用时间步 $t-1$ 的概率密度估计产生时间步 $t$ 的采样，我们可以使用另一个来自热力学的概念， ‘Langevin dynamics’。根据 stochastic gradient Langevin dynamics[2], 我们可以仅通过在马尔科夫链更新中密度函数的梯度更新系统的新状态。基于之前的时间步 $t-1$，可以采样新的时间步 $t$

\[x_t = x_{t-1} + \frac{1}{2} \nabla_x p(x_{t-1}) + \sqrt{1} z_i \qquad z_i \thicksim N(0, 1)\]

上述推导足以预测后续的状态，然而，如果我们想要在任意的时间间隔 $t$ 进行采样，而不是经历所有的中间步骤。我们可以通过将上面等式的超参数替换为 $\alpha_t = 1 - \beta_t$ 来实现：

\[q(x_t \mid x_0) = N(x_t; \sqrt{\alpha_t}x_0, (1 - \alpha_t)I)\]

对步长大小为 $\epsilon$, 基于上一状态 $t-1$，可以采样新的状态 $t$：

\[x_t = x_{t-1} + \frac{\epsilon}{2} \nabla_x p(x_{t-1}) + \sqrt{\epsilon} z_i \qquad z_i \thicksim N(0, 1)\]

Reconstruction

相反的过程需要在给定系统当前状态的较早时间步估计概率密度。这意味着要估计 $q(x_{t-1} \mid x_t)$，从而从各向同性(isotropic)高斯噪声中生成数据样本。然而，与前向过程不同的是，从当前状态估计前一个状态需要所有前一个梯度的知识，如果没有一个可以预测这种估计的学习模型，我们就无法获得。因此，我们必须训练一个神经网络模型来基于时间步 $t$ 的当前状态和学习到的权重估计 $p_\theta(x_{t-1} \mid x_t)$。

\[p_\theta(x_{t-1} \mid x_t) = N(x_{t-1}; \mu_\theta(x_t, t)， \Sigma_\theta(x_t, t))\] \[p_\theta(x_{0:T}) = p(x_T) \prod_{t=1}^T p_\theta(x_{t-1} \mid x_t)\]

对均值函数的参数化可由 [3]提出的方法计算：

$\mu_\theta(x_t, t) = \frac{1}{\sqrt{a_t}}(x_t - \frac{\beta_t}{\sqrt{1 - \alpha_t})} \epsilon_\theta(x_t, t)$ [3] 提出使用固定方差函数 $\Sigma_\theta = \beta_t$。时间 $t-1$ 的采样可以计算得到：

$x_{t-1} = \frac{1}{\sqrt{a_t}} (x_t - \frac{1 - \alpha_t}{\sqrt{1 - \alpha_t}}\epsilon_\theta(x_t, t)) + \sigma_t z$

Training and Results

Construction of the Model

扩散模型训练中使用的模型与VAE网络的模式相似，但与其他网络结构相比，它往往更简单和直接。输入层的输入大小与数据维度的输入大小相同。根据网络需求的深度，可以有多个隐藏层。中间层是具有各自激活函数的线性层。最后一层的大小再次与原始输入层相同，从而重构原始数据。在去噪扩散网络中，最后一层由两个单独的输出组成，每个输出分别用于预测概率密度的均值和方差。

Computation of Loss Function

网络模型的目标是优化以下损失函数：

$L = E_q\left(-\log p(x_T) - \sum_{t \geq 1}log \frac{p_{\theta}(x_{t-1} \mid x_t) }{q(x_t \mid x_{t-1})}\right)$ 这个损失函数的推导由 [1] 提出，其根据两个高斯分布之间的KL 散度和一组熵线性组合组成这个损失公式。这简化了计算，并且使实现损失函数变得容易。因此，损失函数变为：

\[L= -E_q(D_{KL}(q(x_{t-1} \mid x_t, x_0) \| p_\theta(x_{t-1} \mid x_t)) + H_q(x_T \mid x_0) - H_q(x_1 \mid x_0) - H_p(x_T))\]

[3] 提出进一步的简化损失函数(将估计 $x_t$ 转化为了估计噪声 $\epsilon$)，损失函数变为：

\[L_{simple} = -E_{t, x_0, \epsilon} (\| \epsilon - \epsilon_\theta(\sqrt{\alpha_t}x_0 + \sqrt{1 - \alpha_t} \epsilon, t) \|^2)\]

Results

通过马尔可夫链添加高斯噪声的正向过程的结果如下图所示。总时间步数为100，而图中显示了生成的序列集中的10个样本。

反向扩散过程的结果如下图所示。最终输出的质量取决于超参数的调整和训练周期的数量。

Conclusion

在本文中，我们讨论了扩散模型的基础，以及它们的实现。尽管扩散模型在计算上比其他深度网络架构要昂贵，但是在某些应用中它们的性能要好得多。例如，最近在文本和图像合成任务中的应用，扩散模型已经优于其他架构[4]。进一步的实现细节和代码可以在以下github存储库中找到：https://github.com/azad-academy/denoising-diffusion-model.git

Reference

Sohl-Dickstein, J., Weiss, E. A., Maheswaranathan, N., & Ganguli, S. (2015). Deep unsupervised learning using nonequilibrium thermodynamics. arXiv preprint arXiv:1503.03585.
Max Welling & Yee Whye Teh. “Bayesian learning via stochastic gradient langevin dynamics.” ICML 2011.
Ho, J., Jain, A., & Abbeel, P. (2020). Denoising diffusion probabilistic models. arXiv preprint arXiv:2006.11239.
Prafulla Dhariwal, Alex Nichol, Diffusion Models Beat GANs on Image Synthesis, arXiv: 2105.05233
Diffusion Models Made Easy

【深度学习】Diffusion Models Made Easy