Abstract
深度神经网络(DNN)在图像恢复方面取得了巨大的成功。
然而，大多数DNN方法被设计成一个黑盒，缺乏透明性和可解释性。
尽管有人提出一些方法将传统优化算法与DNN相结合，但它们通常需要预先定义退化过程或手工制作的假设，使其难以处理复杂和真实的应用。
这篇文章提出了一种用于图像复原的深度泛化展开网络(DGUNet)。
具体地说，在不损失可解释性的情况下，将梯度估计策略集成到 Proximal Gradient Descent(PGD)算法的梯度下降步骤中，驱动它处理复杂和真实的图像退化。
此外，作者在不同的PGD迭代中设计了across proximal mapping 的 inter-stage 信息通路，通过一种多尺度和空间自适应的方式来纠正大多数深度展开网络(DUN)的固有信息损失。
通过整合 flexible gradient descent 和 informative proximal mapping，将迭代PGD算法展开为一个可训练的DNN。
对各种图像恢复任务的广泛实验证明了该方法在最先进的性能、可解释性和泛化方面的优越性。
Related Works
Deep Unfolding Networks
深度展开网络(DUN)的主要思想是，传统的迭代优化算法可以通过一堆循环 DNN 块等价地进行叠加。这种对应关系最初应用于 deep plug-and-play（PNP）方法[44、57、74、92、94]，其利用训练好的 denoiser 隐式地将正则化项 $J(x)$ 表示为去噪问题。在PNP的启发下，DUN方法在特定任务中联作优化可训练的 denoiser，以端到端的方式进行训练。 例如，[16]联合优化了UNet作为ADMM [5]算法中的近似映射。然而，其网络结构与处理预定义图像退化的人工假设的退化假设密切相关。[88]使用 ResUNet 取代了 HQS [27] 算法中的近似映射。然而，退化过程也是手动设计的，其网络需要 scale factor、blur kernel 和 noise level 作为额外的输入，因此性能在很大程度上取决于所提供的 degradation factors 的准确性。[60、73、83]通过已知退化过程的PGD算法[4]解决了压缩感知。此外，由于每个阶段结束时的特征到图像的转换，大多数DUN方法都受到信息丢失的困扰。虽然[48]中的跳跃连接有利于信息传输，但其实现仍然原始，例如，特征融合是通过在近似映射模块的单个解码器层上串联来实现的。
Methodology
Traditional Proximal Gradient Descent
PGD 算法通过一个迭代函数估计等式$3$ 为一个迭代收敛问题：
\[\hat x^k = \arg \max_x \frac{1}{2} \| x - (\hat x^{k-1} - \rho \nabla g(\hat x^{k -1 })) \|_2^2 + \lambda J(x) \tag{4}\]| 其中 $\hat x^k$ 表示第 $k$ 次迭代的输出， $g(·)$表示等式 $3$ 的数据保真度。 $\nabla$ 是微分操作， 齐备步长 $\rho$ 加权。数学上来说， $\hat x^{k-1} - \rho \nabla \frac{1}{2} | y - A\hat x^{k-1} | _2^2$ 是一个梯度下降操作， 剩下的部分 $\hat x^k = \arg \min_x \frac{1}{2} | x - v^k | + \lambda J(x)$ 通过近似映射操作 $prox_{\lambda, J}$ 求解。 因此， 它可分为两个子问题， 梯度下降和近似映射。 |
PGD 算法迭代更新 $v^k$ 和 $\hat x^k$ 直到收敛。 ISTA[4] 是一个典型的基于 PGD 的算法， 其正则项定义为 $l_1$ 范数， $J(x) = | x |1$。 因此， ISTA 中的近似映射通过一个 软阈值函数 得到： $\text{prox}{\lambda, J} (v^k) = \text{sign}(v^k) \max(0, \mid v^k \mid - \lambda)$。 然而， 手工 $l_1$ 正则限制了表征能力， 并且其在其应用限制在少数几个退化已知的任务(例如压缩感知)。 这篇文章专注于改进传统PGD算法，通过具有鲁棒和泛化设计的深层神经网络来展开它。
Proposed Deep Generalized Unfolding Network
所提出的 DGUNet 的整个网络结构如图 2 所示， 其是一个基于 DNN 的 PGD 算法的展开框架。 DGUNet 由几个重复的阶段组成。 每个阶段包含一个 flexible gradient descent module(FGDM) 和 informative proximal mapping module(IPMM), 分别对应 PGD 算法一次迭代步骤中的梯度下降和近似映射。 默认情况下，阶段数设置为7个，除第一个和最后一个阶段外，它们共享相同的参数。为了进一步提高模型性能，还提出了一个加号版本，称为DGUNet+，其中所有阶段都与参数独立。
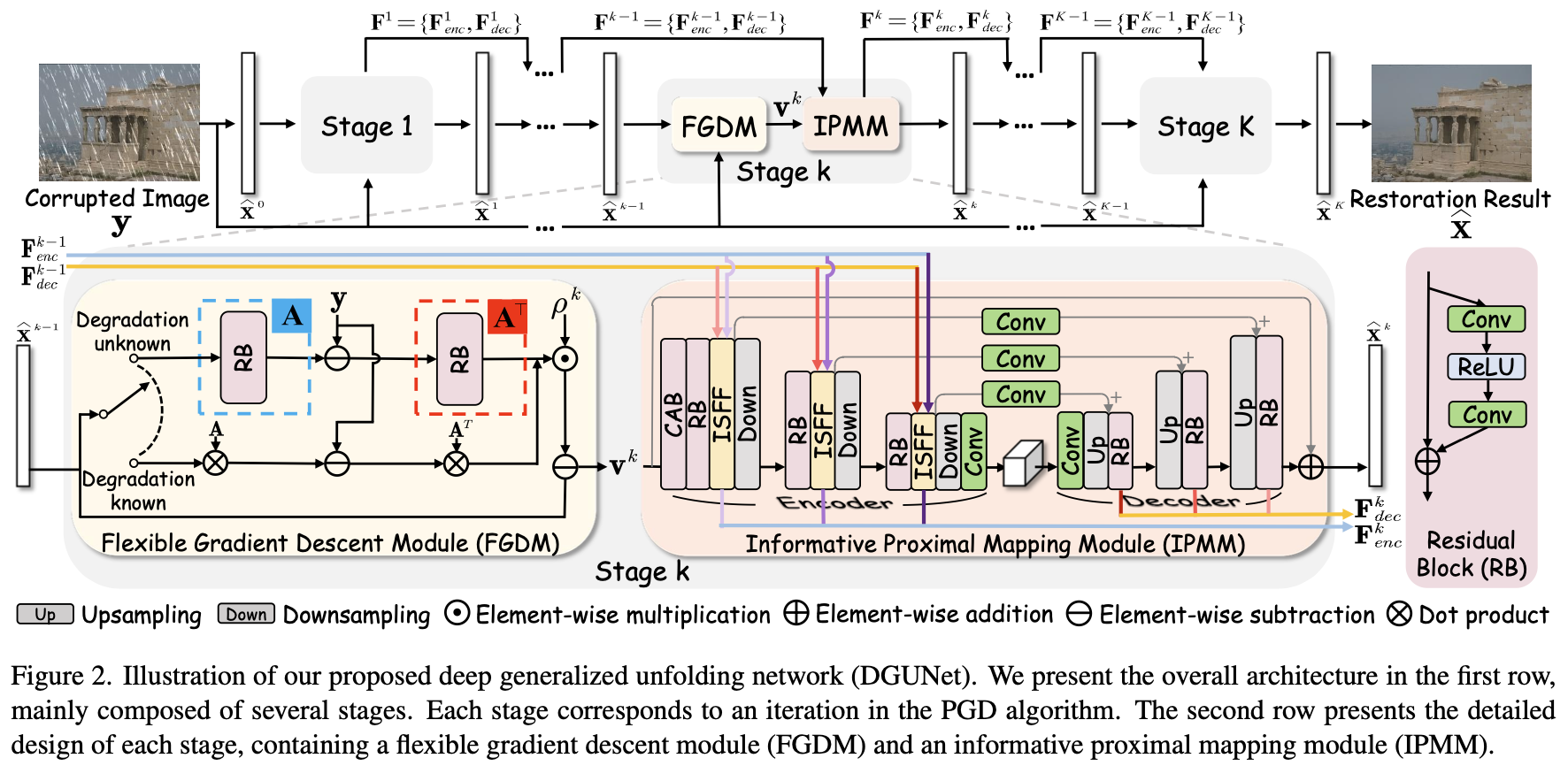
Flexible Gradient Descent Module. 如等式 (5a) 解释， 当退化矩阵 $A$ 已知， 梯度下降步骤是很容易解决的。然而， 当在一些退化问题 $A$ 未知， 使得 $A^T(A \hat x^{k-1} - y)$ 梯度计算不可解。在这种情况下， 这篇文章提出一个 flexible gradient descent module(FGDM)， 如图 2 第二行所示。它有两个模型设置来合理处理已知和未知的退化情况。
如果 $A$ 已知， 直接使用准确的 $A$ 计算梯度。 为了提升鲁棒性， 令步长 $\rho$ 在每个 stage 中设置为可训练的参数， 最终变成如下的梯度下降操作：
\[v^{k} = \hat x^{k-1} - \rho^k A^T (A \hat x^{k-1} - y) \tag{6}\]如果 $A$ 是未知的， 相比于为不同的退化问题制作任务特定的假设， 采用一个数据驱动的策略预测梯度。 利用两个独立的残差块， 叫做 $F_A^k$ 和 $F_{A^T}^k$ 来模拟第 $k$ 个阶段的 $A$ 和它的转置 $A^T$。 梯度被计算为 $F_{A^T}^k(F_A^k(\hat x^{k-1}) - y)$。 因此， 在不损失可解释的情况下, 在退化未知时， DGUNet中的梯度下降可以被定义为：
\[v^k = \hat x^{k-1} - \rho^k \mathcal{F}^k_{A^T}(\mathcal{F}_A^k(\hat x^{k-1}) - y) \tag{7}\]Informative Proximal Mapping Module. 对于等式 $5b$ 的解， 以贝叶斯的角度来看， 它对应于一个去噪问题。 在这个情况下， 设计了如图2所示的 infromative proximal mapping module(IPMM)。 IPMM 是一个 UNet 类型的结构， 有一个编码器和一个解码器组成， 以利用多尺度的特征图。 IPMM 首先以一个 channel attention block(CAB) 来提取浅层特征。 然后使用不带 BN 层的 residual block(RB) 提取三个尺度的特征。 使用 $F_{enc}^k = \left{F^k_{enc \otimes n}\right}{n=1}^3$ 和 $F{dec}^k = \left{F_{dec \otimes n}^k\right}_{n=1}^3$ 来表示从第 $k$ 个阶段第 $n$ 个尺度提取的特征。为了在 IPMM 中切换尺度， 使用步长为 $2$ 的 $2 \times 2$ 的最大池化层用于降采样， 使用卷积层后双线性插值用于上采样。 与其他 denoiser 相似， 使用从输入到输出的全局 pathway， 其鼓励网络通过低频信息。 在 IPMM 的末端， 使用 supervised attention module(SAM) 提取干净的特征并且通过 subspace projection 将它们插入下个阶段。
考虑到大多数DUN方法的 intrinsic information 损失，设计了每个scale 的 inter-stage information pathways，以在不同 stage 从编码器和解码器广播有用的信息。在图2中使用不同颜色的线来分辨不同 scale 的编码器和解码器信息。为了融合 inter-stage 信息，我们在编码器的每个 scale 上设计了一个 inter-stage feature fusion submodule（ISFF）。由于编码器和解码器之间的跳跃连接，inter-stage 信息也可以自然地传播到解码器。ISFF 的结构如图 $3$ 所示， 其收到 [51, 66] 的启发。具体来说，在每个尺度上，将编码器和解码器特征从上一 stage 传输到当前 stage。
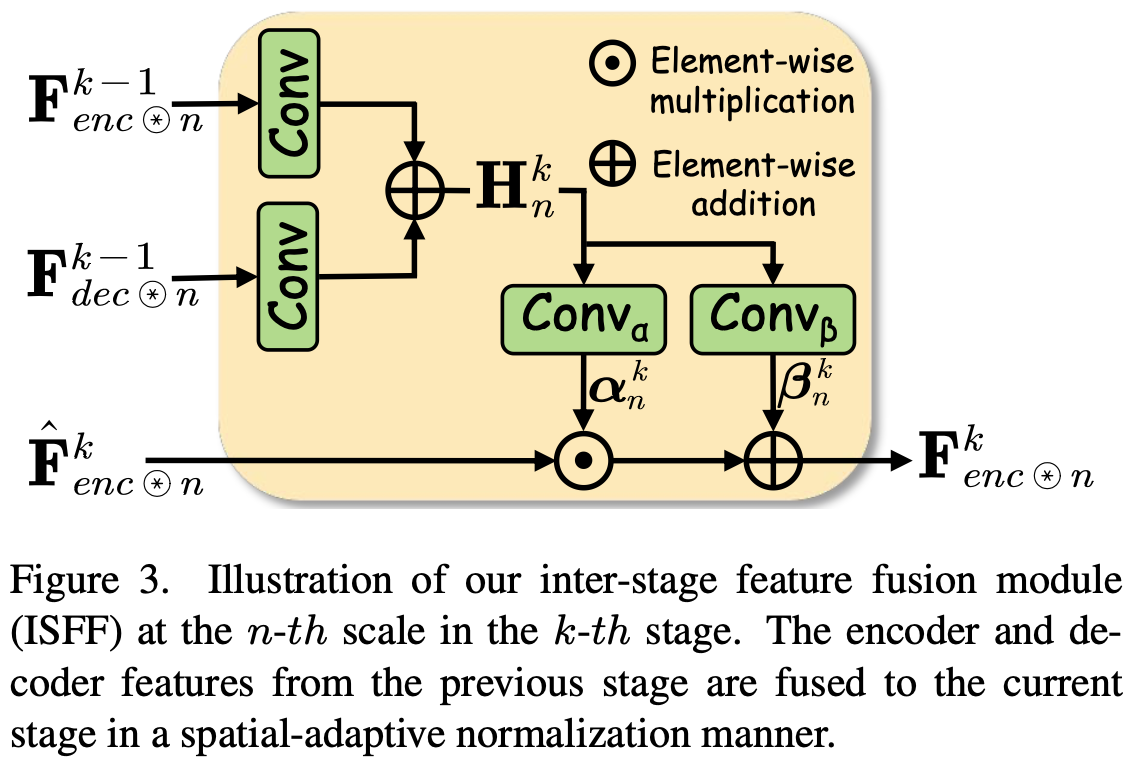上述的特征融合过程是一个标准的 spatial-adaptive normalization。 与 conditional normalization 方法不同， $\alpha_n^k$ 和 $\beta_n^k$ 不是向量， 而是具有空间维度的张量。通过这种方式， 编码器和解码器得到多尺度到的特征， 每个 scale 的特征图保留了之前 stage 的空间信息。 使用 $F^k$ 表示多尺度编码器和解码器特征集合， $F^k = \left{F^k_{enc}, F_{dec}^k\right}$。最终， 等式 $5b$ 中的 IPMM 表达式为：
\(\hat x^k, F^k = \text{prox}_{\theta^k} (v^k, F^{k-1}) \tag{9}\) 其中 $\theta_k$ 表示 IPMM 第 $k$ 个阶段的参数。
Loss Function Design
在所有的 stage 使用 $l_2$ 损失函数优化 DGUNet 和 DGUNet+。 给定一个退化 measurement y 和 ground-truth 图像 $x$， 训练的目标可以定义为：
\(\mathcal{L}(\Omega) = \sum_{k=1}^K \| x - \hat x^k \|_2^2 \tag{10}\) 其中 K 为 stage 数量。 $\hat x^k$ 为每个阶段输出的结果， $\Omega = \left{\rho^k, \mathcal{F}A^k(·), \mathcal{F}{A^T}^k(·), \theta^k\right}_{k=1}^K$ 是DGUNet 的可训练参数。
Conclusion and Discussion
本文提出了一种用于图像复原的深度泛化展开网络(DGUNet)。
开发的原则旨在结合基于模型的方法和深度学习方法的优点。
为此，将PGD优化算法展开到一个深度网络中，并将梯度估计策略集成到梯度下降步骤中，使其易于应用于复杂和真实的应用。
为了弥补DUN中固有信息的损失，设计了多尺度和空间自适应归一化的阶段间特征路径。
在众多图像复原任务上的广泛实验(包括十二个综合和真实测试集)证明了该方法在性能、可解释性和泛化性方面的优越性。
Summary
图像退化过程可以定义为：
\[y = Ax + n \tag{1}\]其中 $y$ 为退化观测， $x$ 是原始图像， $A$ 是退化矩阵， $n$ 表示加性噪声。
求解等式 $1$ 可以使用贝叶斯估计：
\[\hat x = \arg \max_x \log P(x \mid y) = \arg \max_x \log P(y \mid x) + \log P(x) \tag{2}\]数据保真项通常定义在 $l_2$ 范数下， 将等式 $2$ 表示为一下能量函数(损失函数？)：
\[\hat x = \arg \min_x \frac{1}{2} \|y - Ax \|_2^2 + \lambda J(x) \tag{3}\]通过 PGD 算法估计等式 $3$ 可以将其视为一个迭代收敛问题：
\[\hat x^k = \arg \min_x \frac{1}{2} \| x - (\hat x^{k-1} - \rho \nabla g(\hat x^{k-1})) \|_2^2 + \lambda J(x) \tag{4}\]$g(·)$ 是等式 $3$ 中的数据保真项(l2范数？)。也就是?
\[\hat x^k = \arg \min_x \frac{1}{2} \| x - (\hat x^{k-1} - \rho \nabla \frac{1}{2}\|y - A\hat x^{k-1}\|_2^2) \|_2^2 + \lambda J(x) \tag{4}\]其中 $\rho$ 是学习率。
上式 $\hat x^{k-1} - \rho \nabla \frac{1}{2}|y - A\hat x^{k-1}|_2^2$ 是一个梯度下降操作：
\(v^k = \hat x^{k-1} -\rho A^T (A\hat x^{k-1} - y) \tag{5a}\) 剩下的部分 $\hat x^k = \arg \min_x \frac{1}{2} |x - v^k| + \lambda J(x)$ 通过近似映射操作 $prox_{\lambda, J}$ 求解：
\[\hat x^k = prox_{\lambda, J}(v^k) \tag{5b}\]PGD 算法迭代更新 $v^k$ 和 $\hat x^k$ 直到收敛。
-
Previous
【深度学习】Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning -
Next
【深度学习】COAST：COntrollable Arbitrary-Sampling NeTwork for Compressive Sensing
