Abstract

Snapshot compressive imaging(SCI)系统旨在利用2D detectors 在单次拍摄中捕捉高维(3D)图像。

SCI设备包括两个主要部分:硬件编码器和软件解码器。

硬件编码器通常包括一个(光学)成像系统，旨在捕捉 compressed measurements。

另一方面，软件解码器指的是一种重建算法，从这些 measurement 中检索所需的高维信号。

这篇文章利用深度展开的思想，提出了一种基于 generalized alternating projection(GAP-Net) 算法的SCI恢复算法——GAP-Net。

在每个阶段，GAP-Net通过一个训练好的卷积神经网络(CNN)来传递它对期望信号的当前估计。

CNN作为去噪器，将估计结果投影回所需的信号空间。

对于采用训练好的基于自编码器的 denoiser 的 gap 网络，作者证明了一个概率的全局收敛结果。

最后，作者研究了 GAP-Net 在解决视频 SCI 和光谱 SCI 问题中的性能。

在这两种情况下，GAP-Net 在合成数据和真实数据上都显示出具有竞争力的表现。

除了具有较高的精度和速度外，作者还展示了GAP-Net 对信号调制的灵活性，这意味着训练好的 GAP-Net 解码器可以应用于不同的系统。

Introduction

人工智能和机器人技术的最新发展对计算效率高的高维(HD)数据捕捉和处理设备产生了前所未有的需求。然而，现有的光学传感器通常只能直接捕获不超过二维(2D)信号。捕捉三维或更高维度的信号仍然具有挑战性，因为直接执行三维数据采集的传感器还不存在。

近年来，利用 2D detector 捕捉 HD(3D)信号的快照压缩成像(SCI)系统被证明是解决这一挑战的一个有前途的解决方案。与传统摄像机不同，SCI系统根据 sensing matrix 对一组连续的图像视频帧(如CACTI[21])或光谱通道(如CASSI[39])进行采样，并沿着时间或频谱对这些采样信号进行集成，以获得最终的压缩 measurements 值。使用这些技术， SCI 系统能够以低内存、低带宽、低能量、低成本捕获高速运动或高分辨率光谱信息。

在SCI系统中有两个主要组成部分:硬件编码器和软件解码器。硬件编码器通常是一个(光学)成像系统，用于捕获所需信号的压缩 measurements 值，而软件解码器则是指从这些 measurements 值中恢复所需高清数据的算法。该硬件编码器的基本原理是使用比相机捕获率更高的速度调制HD数据。为了实现这一目标，通常使用编码孔径(binary mask)或其他空间光调制器。这篇文章重点研究了软件解码器，即重构算法， 直到最近由于现有重构算法缓慢的速度阻碍了SCI的广泛应用。由于深度学习的发展，近年来各种基于卷积神经网络(convolutional neural networks, CNNs)的SCI恢复算法[30]，[42]，[23]，[5]被开发出来。与之前的方法相比，这些算法显著加快了重构过程。

SCI重构算法可分为以下四类：

• 设计基于迭代优化的算法，假设源结构由(典型的简单)先验(或正则化函数)捕获，如 sparsity [47] 或 total variation(TV)
• 端到端CNNs (E2E-CNNs)，使用大量训练数据进行训练，这些数据包括 measurements 数据和(可选) mask 作为输入，ground truth 即底层期望信号作为输出;在测试过程中，将捕捉到的 measurements 数据输入到训练好的E2E-CNN中，它有望瞬间产生所需的信号。
• 深度展开算法，其中，不是一个CNN，而是训练一系列K个CNN，将 measurements 映射到所需信号[22]，[41];与E2E-CNNs不同，这里，每个阶段由两部分组成: i)线性变换和 ii)通过一个作为去噪器的CNN传递信号
• 即插即用(PnP)方法[36]，[37]，将预训练好的去噪网络插入类(a)[30]，[51]的迭代算法之一。

基于迭代优化的方法已经在文献中广泛研究了各种各样的先验集。这种算法的速度和质量是不同的，更快的版本(例如，那些使用TV[1]，[50])通常不能实现高重建质量，高性能版本通常是非常慢的[20]。然而，即使是类(a)相对较快的算法，目前也比类(b)-(d)[30]基于cnn的算法要慢得多。E2E-CNN算法需要大量的训练数据集、较长的训练时间和较大的GPU内存。在某些应用程序中，这是不可行的，例如在处理大规模数据集[51]时。由于PnP算法不需要对网络进行再训练，因此具有灵活性，可用于大规模数据集。但是，它们的性能主要受限于预训练的去噪网络。例如，高效灵活的高光谱图像去噪算法目前还没有。

Related Work

基于优化的SCI算法，如TwIST[1]、GAP-TV[50]、GMM[46]、[45]和DeSCI[20]，使用了不同的先验。DeSCI 使用weighted nuclear nrom 最小化视频帧中的非局部相似 patches 到 ADMM 框架中。DeSCI虽然可以恢复清晰的图像，但恢复8帧(每帧大小为256 x 256)大约需要2个小时，这阻碍了它的广泛应用。受最近基于深度学习的解决方案在图像恢复[44]，[56]上的成功启发，近年来，研究人员也探索了深度学习在计算成像中的应用。深度展开(或展开)[11]已被用于压缩感知(CS)，各种 solver 如ADMM-net[48]、ISTA-net[55]和学习的 D-AMP[25] 已被提出。对于E2E-CNN，[5]中提出的循环神经网络(RNN)现在可以提供与视频SCI的DeSCI一样有竞争力的结果，[23]中提出的光谱模型可以获得最好的光谱SCI结果。

深度展开也被用于视频SCI的[18]，[9]，[22]和光谱SCI[41]。然而，这些方法的灵感来自于每个阶段的稀疏编码，所得到的真实数据重构质量较低。 此外，这些算法还没有收敛性保证。最近的论文[18]采用了在每个阶段使用去噪的类似想法。然而，这些文章仅对视频SCI进行了探讨，并没有对所提出的方法进行理论分析。

注意，现有的模型是为视频SCI或光谱SCI开发的。例如，在视频SCI中使用 RNN 是合理的，但将 RNN 应用于光谱SCI并不直观。这篇文章的目标是开发一个统一的模型，有效地工作在视频SCI和光谱SCI。

基于不同方法的优缺点，这篇文章提出了一种深度展开的SCI恢复算法——GAP-net。下面是稍后将详细描述的GAP-net的一些关键属性：

• GAP-net是一种采用广义交替投影(GAP)[19]框架的深度展开算法。GAP是一种比ADMM[51]更有效的SCI重建框架。
• GAP-net是一种用于视频和光谱SCI的恢复算法，它将解码器每一阶段训练好的CNN作为去噪网络。这与学习的D-AMP[25]恢复图像CS和[18]恢复视频SCI的方法是一样的。文献中还存在其他基于深度展开的SCI恢复算法。在这种方法中，展开的每个阶段的CNN都包含了转换(通过卷积或全连接神经网络实现)和收缩(通过ReLU等实现)。
• 基于上述去噪角度，GAP-net与SCI[51]的PnP框架有关。作者从理论上证明了它的收敛性，并通过实验验证了它的收敛性。
• GAP-net在用合成数据和真实数据(视频SCI和光谱SCI)完成的实验结果中实现了最先进的(在某些情况下，具有竞争力)性能。

Video SCI and Spectral SCI

图2描绘了视频(左)和光谱(右)SCI的原理图。如前所述，两者的基本原理是使用比相机捕获率更高的速度来调制数据立方体。在视频SCI中，提出了不同的调制方案，如 shifting mask[21]和不同的digital micromirror device(DMD)模式[12]，它们都是 active modulation 方法。另一方面，在光谱SCI中，调制可以通过固定 mask 加 disperser [39]实现，这是一种被动调制方法，因此具有更高的能量效率。关键的思想是，使用 disperser，固定的调制模式可以改变不同的波长。

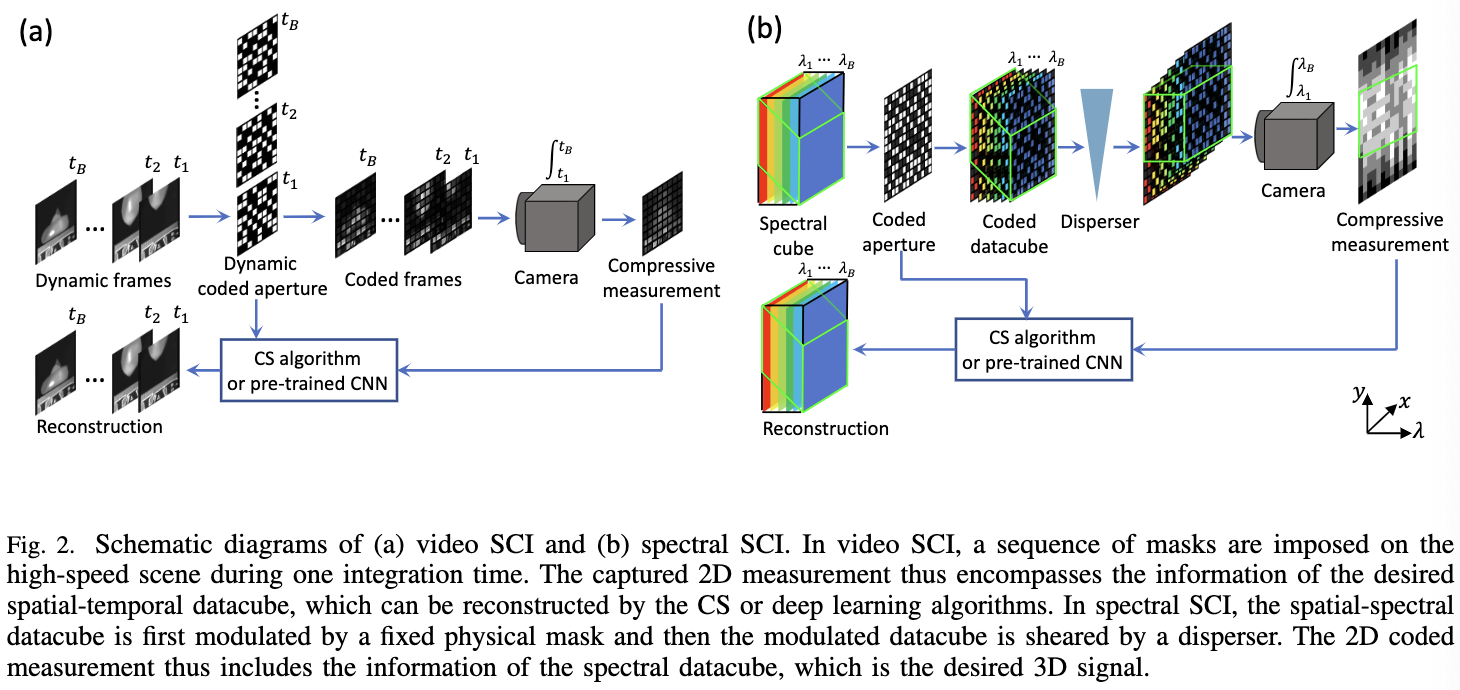
Froward Model of Video SCI

考虑到 video SCI 编码器， 其中一个 $B$ 帧的视频 $X \in \mathbb{R}^{n_x \times n_y \times B} $ 被调制 并被 $B$ 个 sensing matrices(mask) $C \in \mathbb{R}^{n_x \times n_y \times B}$ 映射到单个 measurement 帧 $Y \in \mathbb{R}^{n_x \times n_y}$：

其中 $Z \in \mathbb{R}^{n_x \times n_y}$ 表示噪声； $C_b = C(:, :, b)$ 以及 $X_b = X(:, :, b) \in \mathbb{R}^{n_x \times n_y}$ 表示第 $b$ 个 sensing matrix(mask)。 使用向量化操作， 定义 $y = Vec(Y) \in \mathbb{R}^{n_x n_y}$ 和 $z = Vec(Z) \in \mathbb{R}^{n_x n_y}$。 相似地， 定义 $x \in \mathbb{R}^{n_x n_y B}$ ：

有了上述定义， measurement 处理过程可定义如下：

与标准的压缩感知不同， sensing matrix $H \in \mathbb{R}^{n_xn_y \times n_xn_yB}$ 在 video SCI 中是高度结构化和稀疏的。更具体地，它可以写成 $B$ 个矩阵的对角拼接：

其中， 对于 $b = 1, …, B$， $D_b = \text{diag}(Vec(C_b)) \in \mathbb{R}^{n \times n}$， $n=n_xn_y$。

Forward Model of Spectral SCI

图2(b) 展示了 spectral SCI 系统的图。 令 $X^0 \in \mathbb{R}^{n_x \times n_y \times n_\lambda}$ 和 $M^0 \in \mathbb{R}^{n_x \times n_y}$ 表示原始的 spectral cube 和 固定的 mask modulation。 在场景 $X^0$ 通过 mask 后， 令 $X’ \in \mathbb{R}^{n_x \times n_y \times n_\lambda}$ 表示调制后的版本， 其中不同的波长分别被单独调制， 例如， 对于 $b = 1, …, n_\lambda$， 有：

在通过 disperser 后， cube $X’$ 被 tilted 并且沿着 y 轴 sheared。 令 $X’’ \in \mathbb{R}^{N_x \times (N_y + N_\lambda - 1)\times N_\lambda} $ 表示 tilted cube 并且假设 $\lambda$ 是相关的波长， 例如 $X’(:, :, n_{\lambda_c})$ 是没有沿着 y 轴 sheared 的图像， 则有：

其中 $(u, v)$ 表示在 detector plane 上的坐标系统， $\lambda_b$ 是第 $b$ 个通道的波长， $\lambda_c$ 表示中心波长。 $d(\lambda_b - \lambda_c)$ 表示第 $b$ 个通道的空间移位。

考虑到 detector sensor 集成了波长 $\left[\lambda_{min}, \lambda_{max}\right]$ 所有的光， 压缩的 measurement 在 detector $y(u, v)$ 位置上可以写作：

其中 $x’’$ 表示 $X’’$ 的模拟(连续)表示。

在离散的版本中， 捕获的 2D measurements $Y \in \mathbb{R}^{n_x \times (n_y + n_\lambda - 1)}$ 可以写作：

为了方便描述， 进一步使 $C \in \mathbb{R}^{n_x \times (n_y + n_\lambda - 1) \times n_\lambda}$ 表示为对应不同波长 mask $M^0$ 的移位后的版本：

相似地， 对于不同波长的每个信号帧， 位移后的版本为 $X \in \mathbb{R}^{n_x \times (n_y + n_\lambda - 1) \times n_\lambda}$

紧接着， measurement $Y$ 可以被表示为：

Vectorized Formulation 令 $vec(·)$ 表示矩阵向量化操作。 例如拼接一个矩阵的列为一个向量。 然后， 我们定义 $y = vec(Y), z = vec(Z) \in \mathbb{R}^{n_x(n_y + n_\lambda - 1)}$

其中，对于 $b = 1, …, n_\lambda$, $x^{(b)} = vec(X(:, :, b))$。

此外， 我们定义 sensing matrix:

\(H = [D_1, ..., D_{n_\lambda}] \in \mathbb{R}^{n \times n_\lambda n} \tag{13}\) 其中 $n = n_x(n_y + n_\lambda - 1)$, $D_b = \text{Diag}(\text{vec}(C(:, :, b)))$ 是对角矩阵， $\text{vec}(C(:, :, b))$ 是它的对角元素。至此，我们可以重写公式 $11$ 为：

这在 video SCI 中同样适用。唯一的区别是 measurement 是 $Y \in \mathbb{R}^{n_x \times (n_y + n_\lambda - 1)}$, 然后我们复原 $X$， spatial-spectral cube 通过将$X$ 的每个通道移动回他原始的位置得到 $X^0$。

GAP-Net for SCI

一个 SCI 重建系统的目标是解决如下优化问题：

其中 $\Omega(x)$ 是正则项， 其用来捕获源结构。 为了求解 $15$， 这篇文章提出了 GAP-Net 算法，它利用了 deep unfolding 和 generalized alternating projection 的思想。 GAP-Net 同样受启发于 PnP 框架， 但与 PnP 不同的是， 在算法的每个阶段训练一个不同的去噪网络以提供高保真的重建以及高度的灵活性。

特别地， GAP-Net 如图3所示包含 K 个阶段。 在阶段 $k$, $k = 1, …, K$, 用 $v^{(k)}$ 表示目标信号的当前估计。 用 $x^{(k)}$ 表示一个与 $v^{(k)}$ 维度相同的辅助向量。GAP-Net 按如下方式更新 $v^{(k)}$ 和 $x^{(k)}$：

• 更新 $x$: $x^{(k)}$ 通过在线性流形 $\mathcal{M}$上 $v^{k}$ 的欧几里得投影得到: $y = Hx$。

\(x^{(k + 1)} = v^{(k)} + H^T(HH^T)^{-1}(y - Hv^{(k)}) \tag{16}\) 回忆 $(4)$， $R \mathop{=}\limits_{ }^{def} HH^T$ 是对角矩阵， 因此其逆可以直接得到。

• 更新 $v$: 在投影之后， 下一步的目标是将 $x^{(k+1)}$ 更接近想要的信号域。 在 GAP-Net 中这是由使用一个合适的训练好的去噪器 $D_{k+1}$ 做到的， 令：

GAP-Net 和这篇文章提出的 re-purposed ADMM-Net(图4) 不同于原始的 ADMM-Net， deep-tensor-ADMM-Net 和 tensor-FISTA-Net， 这些网络的目标是在每个阶段模拟稀疏编码， 例如引入变换(由神经网络学习并且通常使用全连接或卷积网络)和收缩(由ReLU实现)。接下来我们比较 GAP-Net 和 ADMM-Net。

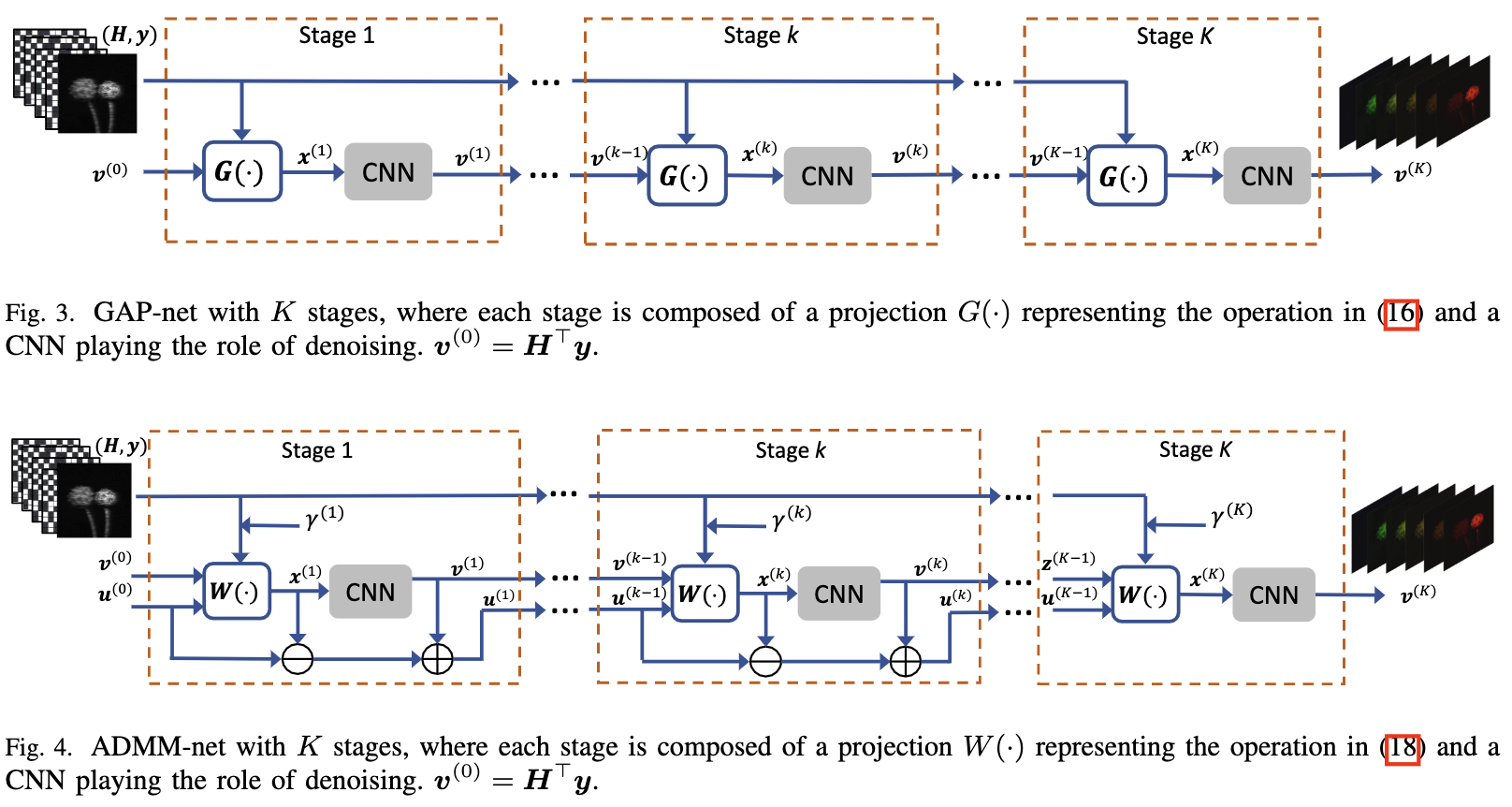
GAP-Net vs ADMM-Net

在不丢失细节的情况下， 我们列出 ADMM-Net 每个阶段的三个步骤：

• 通过 $x^{(k + 1)} = \arg \min_x \frac{1}{2} | y - Hx|_2^2 - (z^{(k)} + u^{(k)}|_2^2$ 解 $x$。 其 close form 解为：

由于 $H$ 的特殊结构， 这可以以 one shot 求解

• 通过 $v^{(k + 1)} = \arg \min_v [\frac{\gamma}{2}|v - (x^{(k + 1)} - u^{(k)})|_2^2 + \tau \Omega(v)]$。 在GAP-Net， 可以通过 CNN 去噪求解

\(v^{(k+1)} = D_{k+1}(x^{(k+1)} - u^{(k)}) \tag{19}\)

• 通过 $u^{(k + 1)} = u^{(k)} - (x^{(k + 1) }- v^{(k+1)})$ 更新辅助变量 $u$。

ADMM-Net 的流程图如图4所示。

与图3相比， GAP-Net 有更少的参数和操作， 因此它相比 ADMM-Net 有效率。

Conclusion

这篇文章提出了一种用于快照压缩成像的深度展开技术GAP-Net。

GAP-Net是一个统一的框架，可以在理论上保证收敛性的情况下，在视频和光谱SCI上实现最先进的性能。

它可以为两种系统以每秒超过60帧的速度重构空间大小为 256 x 256 的数据。

实验结果表明，GAP-Net可以嵌入到真实的SCI相机中，提供端到端的实时捕获和重构，可以在实际应用中得到广泛应用。

• Previous
  【深度学习】COAST：COntrollable Arbitrary-Sampling NeTwork for Compressive Sensing
• Next
  【深度学习】ISTA-Net: Interpretable Optimization-Inspired Deep Network for Image Compressive Sensing