Abstract
近年来，高光谱成像(HSI)引起了越来越多的研究关注，特别是基于编码孔径快照光谱成像(CASSI)系统的高光谱成像。
现有的深度HSI重构模型通常是在成对数据的基础上进行训练，以在CASSI中特定的光学硬件 mask 给出的二维压缩 measurements 上检索原始信号，在此期间 mask 在很大程度上影响重构性能，并可以作为控制数据增强的 “model hyperparameter”。
这种 mask-specific 的训练方式将导致硬件错误校准问题，从而为在不同硬件和噪声环境中部署深度HSI模型设置了障碍。
为了解决这一挑战，作者使用完整的变分贝叶斯学习处理为HSI引入 mask 不确定性，并通过受真实硬件启发的 mask 分解对其进行显式建模。
特别地，作者提出了一种新的基于图的自调整(GST)网络，以适应不同硬件中不同空间结构的 mask 的不确定性。
此外，作者开发了一个双层优化框架，以平衡HSI重建和不确定性估计，其负责 mask 的超参数属性。
Methodology
Preliminaries
Hardware miscalibration. Deep HSI models 在参数 $\theta$ 和 mask $m$ 之间存在一种成对关系。但是 $m$ 和 $\theta$ 之间的校准问题将会导致明显的性能下降。考虑到昂贵的训练时间和硬件中存在的各种噪声，这种错误校准问题不可避免地影响了跨真实系统部署深度HSI模型的灵活性和鲁棒性。为了解决这个问题， 将模型 $f_\theta$ 和 多个 mask 一起建模。然而， 用随机 masks 直接训练单个网络不能在没有见过的 masks 上提供满意的表现，因为缺乏探索在 uncertainties 和 不同 mask 结构之间关系。
Mask Uncertainty
建模 mask uncertainty 是有挑战性的， 由于：
- 2D mask 的高维度和 mask set 大小的限制
- mask 中多变的空间结构
受到 mask 值分布的启发， 其峰值为 0 和 1 的高斯分布， 将 mask 分为两部分：
\(m = \tilde m + z\) 假设 $z$ 中的每个像素服从一个高斯分布， 表示为 $p(z) = \mathcal{N}(\mu, \sigma)$。$\tilde m$ 表示具有特定空间结构的二值 mask。
作者通过估计 mask 后验概率 $p(m \mid X, Y)$ 来估计 mask uncertainty， 其中 $X$ 和 $Y$ 分别表示光谱图像和它们对应的 measurements。
为此， 作者旨在学习一个由 $\phi$ 参数化的 variational distribution $q_\phi(m)$ 以最小化 $q_\phi(m)$ 和 $p(m \mid X, Y)$ 之间的 KL 散度， 如 $\min_\phi KL[q_\phi(m) | p(m \mid X, Y)]$， 等价于最小化 evidence lower bound(ELBO)：
\(\max_\phi \mathbb E_{q_\phi(m)}[\log p(X \mid Y, m)] - KL[q_\phi(m) \| p(m)] \tag{4}\) 其中第一项度量重构， 第二项给定 mask 先验 $p(m)$ 正则化 $q_\phi(m)$。 variational distribution $q_\phi(m)$ 定义为以 $m \in \mathcal{M}$ 为中心的高斯分布。
\[q_\phi(m) = \mathcal{N}(m, g_\phi(m)) \tag{5}\]$g_\phi(m)$ 学习 self-tuning variance 来建模 uncertainty。因此， variational noise distribution $q_\phi(z)$ 服从方差为 $g_\phi(m)$ 的高斯分布。 使用重参数技巧， 令 $m’ \thicksim q_\phi(m)$ 是一个采样自 variational distribution 的随机变量， 有：
\(m' = t(\phi, \epsilon) = m + g_\phi(m) \odot \epsilon, \quad \epsilon \thicksim \mathcal{N}(0, 1) \tag{6}\) 将 $m’$ 的值截断在 [0, 1] 之间。
与AutoEncoder相似，将负对数似然 $\mathbb{E}{q\phi(m)}[- \log p(X \mid Y, m)]$ 实现为 $\ell_2$ 损失并且计算它的蒙特卡洛估计：
\[\ell(\phi, \theta; \mathcal{D}) = \frac{N}{B} \sum_{i=1}^B \| f_\theta(y_i, t(\phi, \epsilon_i)) - x_i \|^2 \tag{7}\]其中 $(x_i, y_i) \in \mathcal{D}$， $B$ 表示 mini-batch 大小， $t(\phi, \epsilon_i)$ 表示从 $q_\phi(m)$ 中采样的第 $i$ 个样本。
因为 $p(m)$ 是未知的， 由于 mask 的不同的空间结构， 作者用 $q_\phi(m)$ 的熵估计等式 $(4)$ 中的 KL 项。最终，用以下损失实现 $\text{ELBO}(q(m))$ ：
\[\mathcal{L} (\phi, \theta; \mathcal{D}) = \ell(\phi, \theta; \mathcal{D}) + \beta \mathbb{H}[\log q_\phi(m)] \tag{8}\]其中 $\mathbb{H}[\log q_\phi(m)]$ 通过计算 $\ln (h_\phi(m) \sqrt{2 \pi e})$ 和 $\beta > 0$ 得到， 解释为 variational inference 和 variational optimization 之间的目标函数。
Graph-based Self-Tuning Network
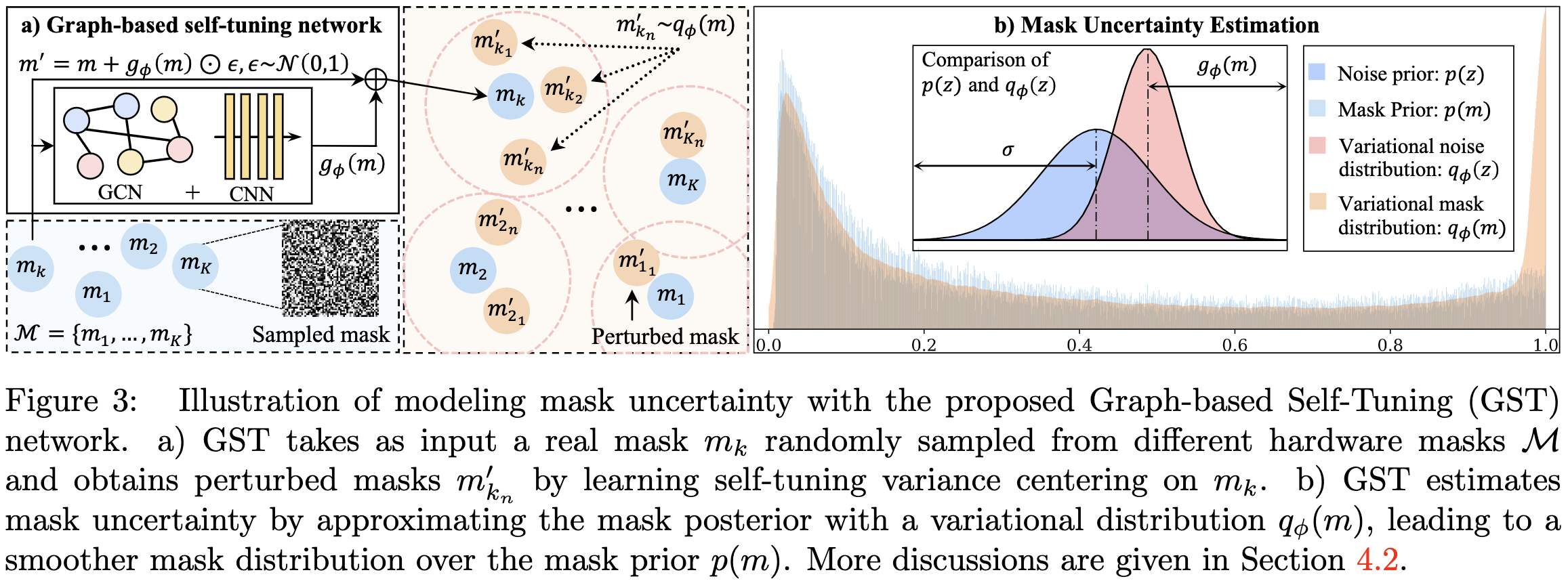
作者提出 graph-based self-tuning (GST) 网络实现等式 $(5)$ 中的 variance model $g_\phi(m)$， 其在每个 mask 附近捕获 uncertainties，并使得 mask 在 real masks 上的分布更光滑， 如图 3 所示。处理没有见过的的 mask(新硬件)的关键是了解如何随着 mask 的空间结构的变化分布。为此，作者将GST实现为视觉推理注意力网络。 它首先基于 neural embedding 计算 pixel-wise correlations(视觉推理)，然后基于图卷积网络(GCN)生成注意力分数。与以往的研究[6,25,61]不同，这篇文章提出的GST模型是针对构建 stochastic probabilistic 编码器来捕获 mask 分布而定制的。
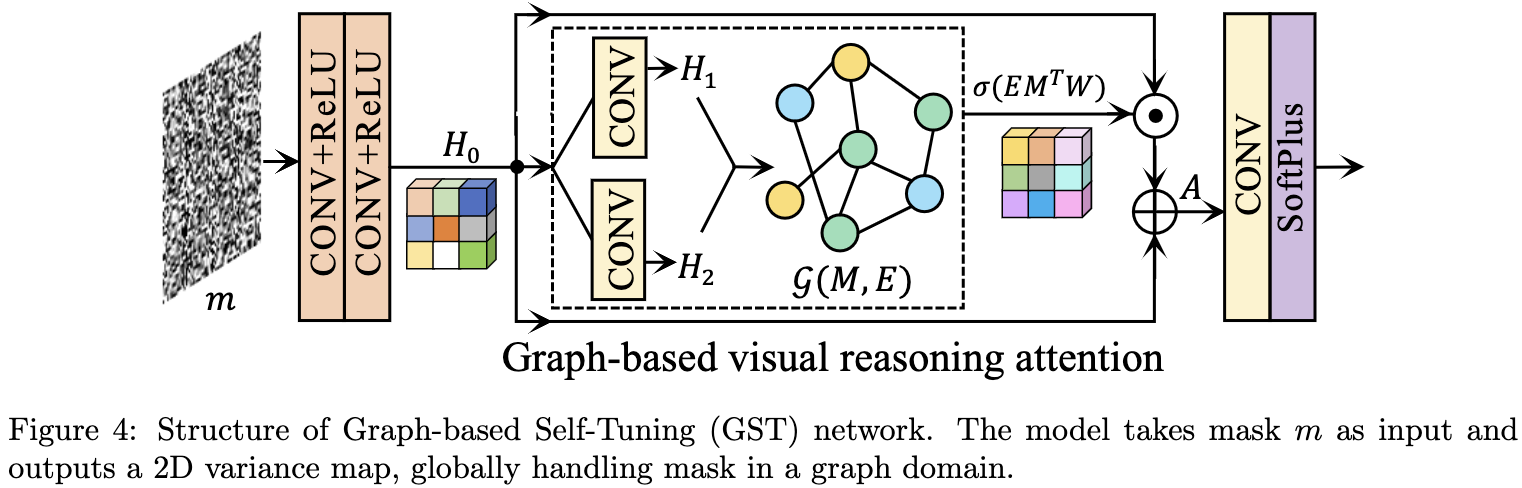
GST 的网络结构如图4所示。给定一个 real mask $m$, GST 使用两个拼接的 $\text{CONV}-\text{ReLU}$ 块生成 neural embedding $H_0$。 然后使用两个 $\text{CONV}$ 层来转换 $H_0$ 为两个不同的 embeddings $H_1$ 和 $H_2$， 通过矩阵乘法 $H_1^TH_2$ 生成一个图表征 $\mathcal{G}(M, E)$, 其中节点矩阵 $M$ 表示 mask 像素， 边矩阵 $E$ 表示 pixel-wise correlations。 用 $W$ 表示 $\text{GCN}$ 的权重矩阵。 通过 pixel-wise 的乘法得到 enhanced attetnion cube：
其中 $\sigma$ 是 sigmoid 函数。最终， self-tuning variance 通过下式得到：
\(g_\phi(m) = \delta(\text{CONV}(A)) \tag{10}\) 其中 $\delta$ 表示 softplus 函数， $\phi$ 表示所有可学习的参数。因此， GST 使得自适应的 variance 建模任意真实 mask。
Bilevel Optimization
尽管使用等式 $(8)$ 中的损失联合训练 HSI 重构网络 $f_\theta$ 和 self-tuning 网络 $g_\phi$ 是可能的， 但将这两个网络的训练表述为 mask 的两个超参数的 bilevel 优化框架更为合适。首先， 深度重构网络对 masks 的改变和扰动是高度敏感的。因此，模型权重 $\theta$ 很大程度上取决于 mask $m$。 其次， 深度 HSI 方法通常使用单个 mask 并且一组 shifting 操作来使得 2D measurement 变成一个多通道的输入， 其中 mask 作为一个数据增强的超参数用于训练深度网络。
具体而言，作者将 low-level 问题定义为HSI重构，high-level 问题定义为 mask uncertainty 估计，并提出 GST模型的最终目标函数如下：
\[\min_\phi \mathcal{L}(\phi, \theta^*; \mathcal{D}^{val}) \quad \text{s.t.} \quad \theta^* = \mathop{\text{argmin}}_\theta \ell(\phi, \theta; \mathcal{D}^{trn}) \tag{11}\]其中 $\ell(\phi, \theta; \mathcal{D}^{trn})$ 由带训练集的等式 $(7)$ 提供， $\mathcal{L}(\phi, \theta^*; \mathcal{D}^{val})$ 在验证集中由等式 $(8)$ 提供。在等式 $(11)$ 中， $f_\theta$ 和 $g_\theta$ 通过计算梯度 $\frac{\partial l}{\partial \theta}$ 和 $\frac{\partial \mathcal{L}}{\partial \phi}$交替更新。为了更好地初始化参数 $\theta$, 作者预训练重构网络 $f_\theta(m, y)$ 几个 epochs。 所提方法的整个训练流程总结为算法 $1$。 引入等式 $(11)$ 有两个好处：
- 它能平衡 HSI 重构和 mask uncertainty 估计
- 它使得所提的 GST 作为一个超参数优化方法， 即便只工作在单个 mask 上， 其也可以提供高保真的重构。
Conclusions
这项工作探索了在真实的CASSI系统中部署深度HSI模型时的一个实际的硬件错误校准问题。
解决方案是通过建模 mask 的不确定性来校准单个重建网络。
受真实 mask 观测的启发，作者提出了一种基于一种可能的 mask 分解的全变分贝叶斯学习方法。
以变分 mask 分布建模和HSI检索为目标，作者引入并实现了一种新的基于图的自调整(GST)网络，该网络在二层优化框架下进行HSI重构和不确定性推理。
该方法实现了平滑分布，并在两种不同的错误校准场景下取得了良好的性能。
