Abstract

全局操作，如全局平均池，被广泛用于顶级性能的图像恢复。

它们通过输入特征沿着整个空间维度聚合全局信息，但在图像恢复任务的训练和推理过程中表现不同:它们基于不同的区域，即裁剪的patch(来自图像)和全分辨率图像。

本文回顾了全局信息聚合，发现推理过程中基于图像的特征分布与训练过程中基于patch的特征分布不同。

这种训练-测试的不一致性会对模型的性能产生负面影响，这是以往研究中严重忽视的问题。

为了减少不一致性，提高测试时的性能，作者提出了一种简单的方法，称为 Test-time Local Converter(TLC)。

TLC只在推断时将全局操作转换为局部操作，这样它们就聚集了局部空间区域内的特征，而不是整个大图像。

该方法可以应用于各种全局模块(如归一化、通道和空间注意力)，且成本可以忽略不计。

在不需要任何微调的情况下，TLC改进了几个图像恢复任务的最先进的结果，包括单图像运动去模糊、视频去模糊、离焦去模糊和图像去噪。

Analysis and Approach

Test-time Local Converter

为了减少训练和测试不一致并提高模型的测试时的性能，作者提出了一种名为 Test-time Local Converter（TLC）的测试时解决方案。

TLC没有改变训练策略或裁剪图像，而是在推理阶段直接更改特征级别的信息聚合区域范围。

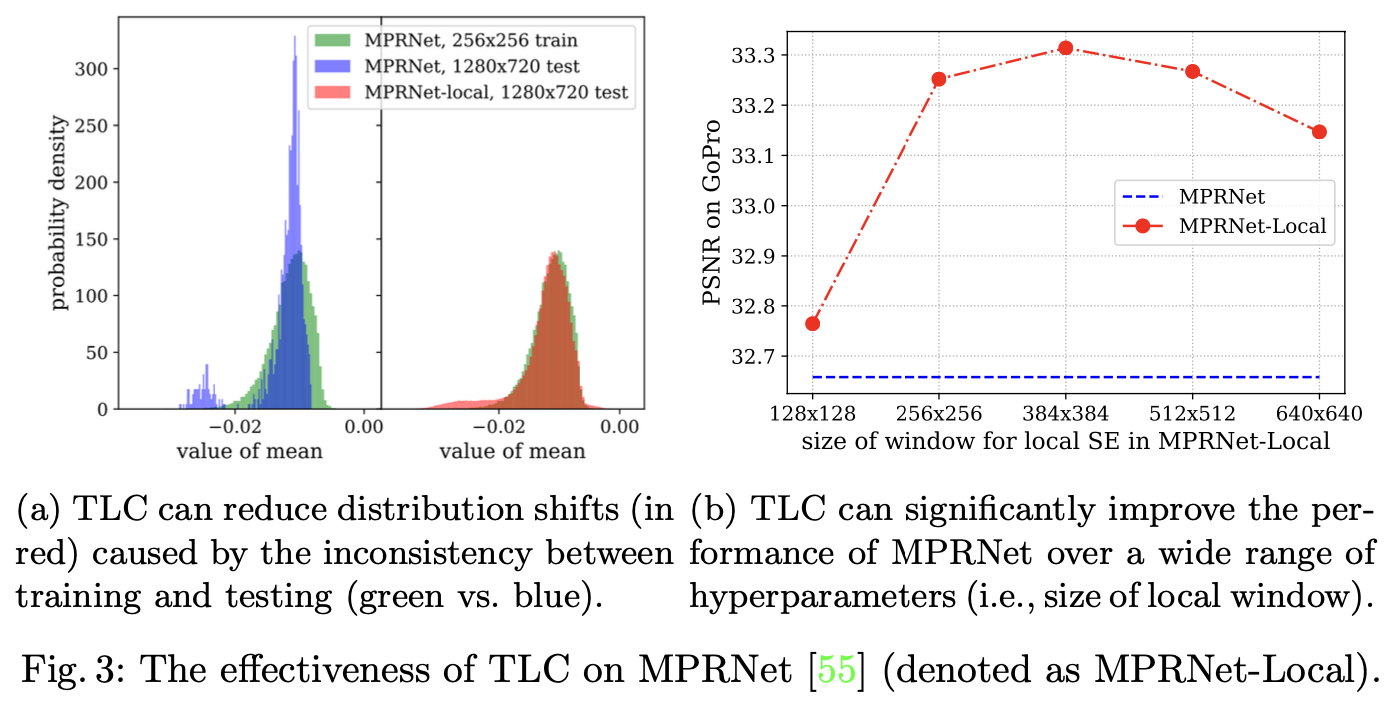
如图1b所示， TLC 将空间信息聚合操作从全局转换为局部，例如，特征的每个像素都会在局部聚合其特征。具体来讲，全局操作的输入特征 $X$ 被分为重叠的 $K_h \times K_w$ 个重叠的窗口大小。然后，信息聚合操作被独立地应用于每个重叠窗口。因此，TLC减少了统计数据分布转移，如图3a所示：在训练阶段(绿色)，MPRNet-Local(红色)获得的统计数据分布接近原始MPRNet。此外，如图2d所示，TLC生成了一个没有边界伪影的清晰图像。

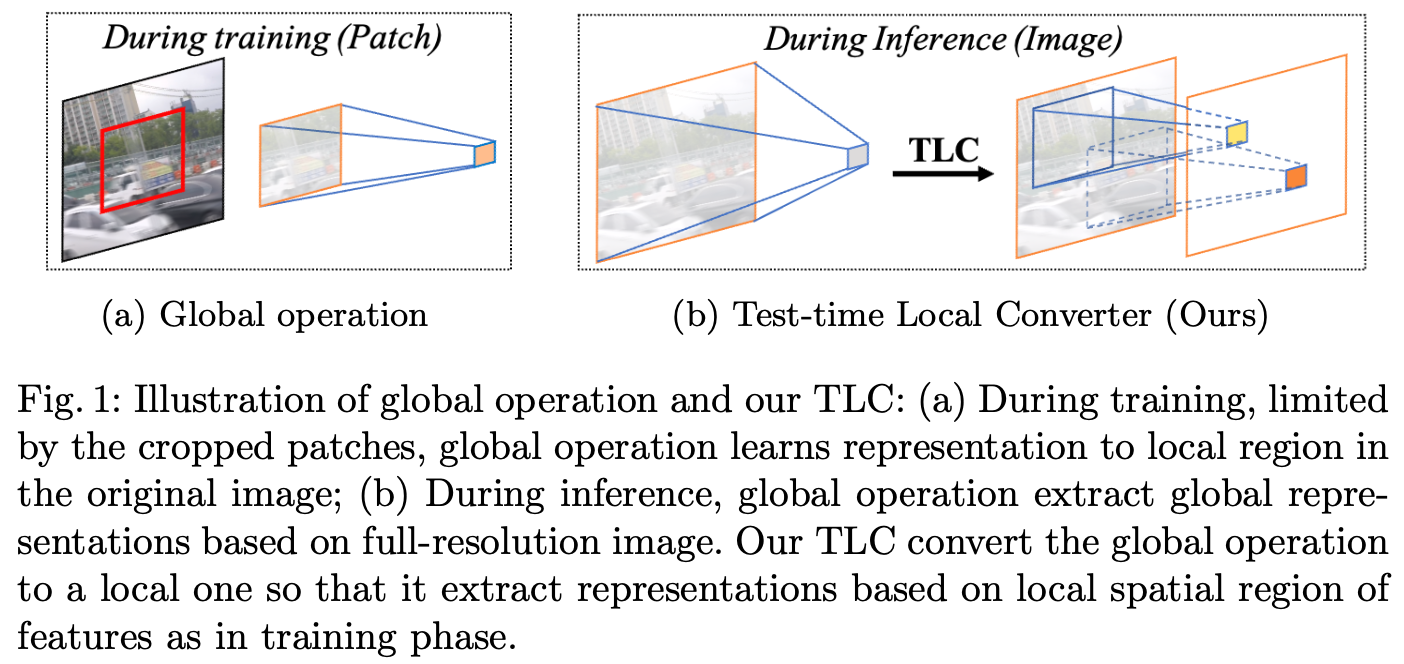
该简单设计的一个优点是，局部处理的高效实现使额外的计算成本可以忽略不计，允许图像恢复器轻松使用 TLC。接下来，作者将讨论求均值操作的实现，这是一个信息聚合的例子，广泛用于图像恢复模型。

Efficient Implementation of Information Aggregation. 一个特征层的全局信息聚合 $X \in \mathbb{R}^{H \times W}$（在不损失泛化性的情况下，忽略通道维度），可以公式化为：

$\Phi(X, f) = \frac{1}{HW} \sum_{p=1}^H \sum_{q=1}^W f(X_{p, q})$ 齐总 $f: \mathbb{R} \rightarrow \mathbb{R}$ 定义信息如何被计算，并且 $\Phi(X, f) \in \mathbb{R}$ 表示聚合的信息。它的计算复杂度是 $O(HW)$。对于局部信息聚合，特征 $X \ \in \mathbb{R}^{H \times W}$ 每个像素在一个局部窗口($K_h \times K_w$)中聚合信息可以公式化为：

$\Psi(X, f)_{i, j} = \frac{1}{K_h K_w} \sum_{p} \sum_{q} f(X_{p, q})$ 其中$(p, q)$ 在局部窗口$(i, j)$ 中， $\Phi(X, f) \in \mathbb{R}$ 表示聚合的局部信息。

实际上，实现 $\Psi(X, f)$ 通过两步。首先，使用步长等于 1 的滑动窗口对每个非边缘的像素聚合局部信息。其次，通过复制边缘填充结果。第一步的计算复杂度为 $O(HWK_hK_w)$。但是在每个局部窗口均值/求和聚合可以认为是子矩阵求和问题，可以以 $O(1)$ 计算复杂度通过前缀和技巧求解。因此，整体复杂性可以降低到 $O(HW)$ ，这与全局信息聚合操作一致。因此， TLC 不是计算瓶颈。

Extending TLC to Existing Modules

这一小节借用了上面定义的符号（例如，$\Phi/\Psi$ 分别表示全局/局部信息聚合运算）。为了拓展 TLC 到现有模块，作者将信息聚合操作从全局转换为局部。在下面，作者以 Squeeze-and-Excitation(SE) 和 Instance Normalization(IN) 为代表，它可以很容易地应用于其他规范化模块，如 Group Normalization(GN) 或者 SE 的变体(例如， CBAM， GE)。

Extending TLC to SE Block. 首先简单回顾 squeeze-and-excitation (SE) 块。对于一个空间大小为 $(H, W)$ 和 $C$ 个通道的特征图 $X \in \mathbb{R}^{H \times W \times C}$， SE块首先压缩全局空间信息到通道，他可以表示为 $\Phi(X^{(c)}, id), \forall c \in [C]$，其中 $id(t) = t, \forall t \in \mathbb{R}$。然后，接下来是一个多层感知器（MLP）来评估通道注意力，从而重新加权特征图。随着全局信息分布的偏移，对全局空间维度的压缩可能不理想。为了解决这个问题，作者通过替换 $\Phi(X^{(c)}, id)$ 为 $\Phi(X^{(c)}, id) \forall c \in [C]$ 拓展 TLC 到 SE 上。与SE一样，然后是沿着通道维度的MLP。不同的是，在这种情况下，特征图被 element-wise 注意力重新加权。

Extending TLC to IN. 对于特征映射 $X \in \mathbb{R}^{H \times W}$（为了简单起见，省略了通道维度），IN 的归一化特征 $Y$ 计算为：$Y = (X − \mu) / \sigma$，其中统计量 $\mu$ 和 $\sigma$ 是在 $X$ 的全局空间上计算的平均值和方差：

$\mu = \Phi(X, id), \sigma^2 = \Phi(X, sq) - \mu^2$ 其中 $id(t) = t, sq(t) = t^2, \forall t \in \mathbb{R}$。此外，可学习的参数 $\gamma, \beta$ 被用于缩放和偏移规范化后的特征 $Y$。在推理期间，作者通过分别替换 $\Phi(X, id)$ 和 $\Phi(X, sq)$ 为 $\Psi(X, id)$ 和 $\Psi(X, sq)$ 。因此，每个像素都被邻域统计信息归一化。

Extending to transposed self-attention. TLC 可以将 Restormer 中的 transpoed self-attention 从全局转换为局部区域。然而，由于GPU内存的低效率和局限性，即每个像素的注意力权重不同，TLC在转换自注意时使用更大的步长而不是步长为1。具体来说，转换的自注意力独立应用于从输入特征切片的 $K_h \times K_w$ 的每个重叠窗口。然后，通过沿着空间维度串联并在重叠区域上平均来融合重叠的输出。

Conclusion

这项工作揭示了由于全局操作的训练-测试不一致，在训练和推断之间的全局信息分布发生了转移，这对恢复模型的性能产生了负面影响。

作者提出了 simple yet test-time 的解决方案，称为 Test-time Local Converter，它取代了从整个空间维度到局部窗口的信息聚合区域，以缓解训练和推断之间的不一致性。

该方法不需要任何再训练或微调，并且提高了模型在各种任务中的性能。

【深度学习】TLC：Improving Image Restoration by Revisiting Global Information Aggregation

Abstract

Analysis and Approach

Test-time Local Converter

Extending TLC to Existing Modules

Conclusion

CATALOG

FEATURED TAGS

FRIENDS