凸优化问题是以下形式：

其中 $f$ 和 $g_i, i =1, …, m$ 都是凸的， $h_j, j=1, …, r$ 是 affine。

特殊的性质： 任意局部最小值都是全局最小值。

Convex sets

$\color{red}{\text{Convex set}}$： $C \subseteq \mathbb R^{n}$ ：

\(x, y \in C \Rightarrow tx + (1 - t)y \in C \quad \text{for all} \quad 0 \leq t \leq 1\) 简单来说，连接任何两个元素的线段完全在集合中

$x_1, …, x_k \in \mathbb{R}^n$ 的$\color{red}{\text{Convex combination}}$ ： 任意线性组合：

$\theta_i \geq 0, i = 1, …, k$， 并且 $\sum_{i=1}^k \theta_i = 1$ 。

集合 $C$ 的 $\color{red}{\text{Convex hull}}$ $\text{conv}(C)$ 是所有元素的 convex combinations。 并且总是凸的。

Examples of convex sets

• 空集， 点， 线
• $\color{red}{\text{Norm ball}}$ : ${x: | x | \leq r}$, 给定范数 $| · |$， 半径为 $r$
• $\color{red}\text{Hyperplane}$ : ${x : a^\top x = b}$， 给定 $a, b$
• $\color{red}\text{Halfspace}$ ： ${x : a^\top x \leq b}$
• $\color{red}\text{Affine space}$ ： ${x ： Ax = b}$， 给定 $A, b$
• $\color{red}\text{Polyhedron}$ ： ${x : Ax \leq b}$， 其中不等号解释为 componentwise
• $\color{red}\text{Simplex}$： plolyhedra 的特殊情况， 给定 $\text{conv}{x_0, …, x_k}$， 其中这些点是 affinely independent 的

Cones

$\color{red}\text{Cone}$： $C \subseteq \mathbb{R}^n$:

$\color{red}\text{Convex cone}$： cone 也是凸的， 例如：

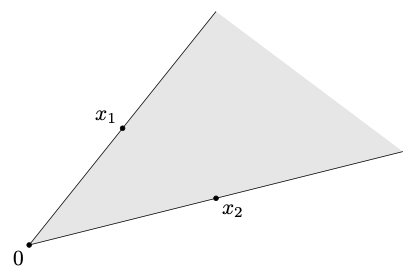
$x_1, …, x_k \in \mathbb{R}^n$ 的 $\color{red}\text{Conic combination}$ ： 任意线性组合：

\(\theta_1 x_1 + ... + \theta_k x_k\) 其中 $\theta_i \geq 0, i = 1, …, k$。

$\color{red}{\text{Conic hull}}$ 是所有 conic combination。

Examples of convex cones

• $\color{red}\text{Norm cone}$: ${(x, t): | x | \leq t}$ ， 对于一个范数 $| · |$。 在 $\ell_2$ 范数 $| · |_2$ 下， 叫做 $\color{red}\text{second-order cone}$
• $\color{red}\text{Normal cone}$： 给定集合 $C$ 和 点 $x \in C$, 我们可以定义：

\(\mathcal{N}_C(x) = \{g : g^\top x \geq g^\top y, \quad \text{for all} \quad y \in C\}\)

• $\color{red}\text{Positive semidefinite cone}$： $\mathbb{S}_+^n = {X \in \mathbb{S} : X \succeq 0}$， 其中 $x \succeq$ 0 表示 $X$ 是 positive semidefinite ($\mathbb{S}^n$ 是 $n \times n$ 对称矩阵的集合)

Key properties of convex sets

• $\color{red}\text{Separating hyperplane theorem}$： 两个不想交的 convex sets 在超平面间有 separating

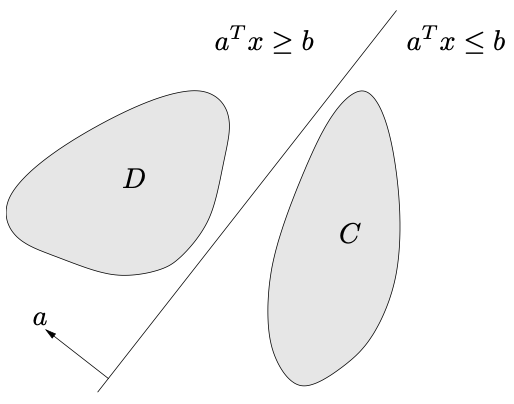
如果 $C, D$ 有非空 convex sets $C \cap D = \emptyset$， 存在 $a, b$ :

• $\color{red}\text{Supporting hyperplane theorem}$： 凸集的边界点有一个支撑超平面穿过它

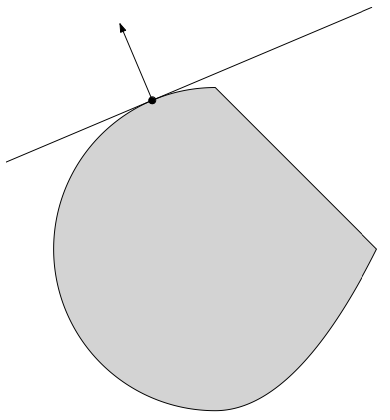
如果 $C$ 是非空 convex set， $x_0 \in \text{bd}(C)$， 存在 $a$:

上述两个定理（seperating 和 supporting hyperplane 定理）都有部分相反；

Operations preserving convexity

• $\color{red}\text{Intersection}$： 凸集的交是凸的
• $\color{red}\text{Scaling and translation}$ ： 如果 $C$ 是凸的， 那么：

\(aC + b = \{ax + b : x \in C\}\) 是凸的， 对于任意 $a, b$

• $\color{red}\text{Affine images and preimages}$： 如果 $f(x) = Ax + b$ 并且 $C$ 是凸的， 那么：

是凸的， 如果 $D$ 是凸的， 那么：

是凸的

Example: linear matrix inequality solution set

给定 $A_1, …, A_k, B \in \mathbb{S}^n$， $\color{red}\text{linear matrix inequality}$ 是如下形式：

\(x_1 A_1 + x_2 A_2 + ... + x_k A_k \preceq B\) 对于变量 $x \in \mathbb{R}^k$。 让我们证明满足上述不等式的点 $x$ 的集合 $C$ 是凸的

Approach 1： 直接验证 $x, y \in C \Rightarrow tx + (1- t)y \in C$。 对于任意 $v$:

Approach 2: 令 $f: \mathbb{R}^k \rightarrow \mathbb{S}^n$， $f(x) = B - \sum_{i=1}^k x_i A_i$。$C = f^{-1}(\mathbb{S}_+^n)$ 是凸集的 affine preimage。

More operations preserving convexity

• $\color{red}\text{Perspective images and preimages}$： perspective function 是 $P: \mathbb{R}^n \times \mathbb{R}{++} \rightarrow \mathbb{R}^n$ (其中 $\mathbb{R}{++}$ 表示正实数)

\(P(x, z) = x / z\) 对于 $z > 0$。 如果 $C \subset \text{dom}(P)$ 是凸的， 那么 $P(C)$ 也是凸的， 如果 $D$ 是凸的， 那么 $P^{-1}(D)$ 也是凸的。

• $\color{red}\text{Linear-fractional images and preimages}$ ：由 affine function 组成的 perspective map:

\(f(x) = \frac{Ax + b}{c^\top x + d}\) 叫做 $\color{red}\text{linear-fractional}$ 函数，定义在 $c^\top x + d > 0$ 上。 如果 $C \subseteq \text{dom}(f)$ 是凸的， 那么 $f(C)$ 也是凸的， 如果 $D$ 是凸的， 那么 $f^{-1}(D)$ 也是凸的

Example： conditional probability set

令 $U, V$ 为在 ${1, …, n}$ 和 ${1, …, m}$ 上的随机变量。 令 $C \subseteq \mathbb{R}^{nm}$ 是 $U, V$ 的联合分布集合， 例如每个 $p \in C$ 定义为联合概率：

\(p_{ij} = \mathbb{P}(U = i, V = j)\) 令 $D \in \mathbb{R}^{nm}$ 包含对应的 $\color{red}\text{conditional distributions}$， 例如，每个 $q \in D$ 定义：

\(q_{ij} = \mathbb{P}(U = i \mid V_j)\) 假设 $C$ 是凸的， 让我们证明 $D$ 是凸的。

Convex functions

$\color{red}\text{Convex function}$ ： $f: \mathbb{R}^n \rightarrow \mathbb{R}$ ， 有 $\text{dom}(f) \subseteq \mathbb{R}^n$ 凸， 并且：

对所有 $x, y \in \text{dom}(f)$

简答来说， 函数在线段 $f(x), f(y)$ 下面

$\color{red}\text{Concave function}：$ 上面不等式的反：

Important modifiers：

• $\color{red}\text{Strictly convex}：$ 对 $x \neq y$ 并且 $0 < t < 1$， $f(tx + (1 - t)y) < tf(x) + (1 - t)f(y)$ 。简单来说，$f$ 是凸的， 并且比线性函数具有更大的曲率。
• $\color{red}\text{Strongly convex}$ : 参数 $m > 0$: $f - \frac{m}{2} | x |_2^2$ 是凸的。 简单来说， $f$ 作为一个二次方程至少是凸的。

Note： $\text{strongly convex}$ $\Rightarrow$ $\text{strickly convex}$ $\Rightarrow$ $\text{Convex}$

Example of convex functions

• Univairate functions:
• • Exponential function： 在 $\mathbb{R}$ 上, 对所有 $a$, $e^{ax}$ 是 convex 的
• • Power function： 在 $\mathbb{R}_+$ 上， 对 $a \geq 1$ 或者 $a \leq 0$ ， $x^a$ 是 convex 的
• • Power function： 在 $\mathbb{R}_+$ 上， 对 $0 \leq a \leq 1$， $x^a$ 是 concave 的
• • Logarithmic function： 在 $\mathbb{R}_{++}$ 上， $\log x$ 是 concave
• $\color{red}\text{Affine function}$： $a^\top x + b$ 同时是 convex 和 concave 的
• $\color{red}\text{Quadratic function}$： 假设 $Q \succeq 0$(positive semidefinite)， $\frac{1}{2} x^\top Q x + b^\top x + c$ 是 convex 的
• $\color{red}\text{Least squares loss}$ ： $|y - Ax|_2^2$ 总是 convex 的 (因为 $A^\top A$ 总是 positive semidefinite 的)
• $\color{red}\text{Norm}$： 对所有范数， $| x |$ 是 convex 的， 例如 $\ell_p$ 范数

包括 operator(spectral) 和 trace(nuclear) 范数

其中 $\sigma_1(X) \geq … \geq \sigma_r(X) \geq 0$ 是矩阵 $X$ 是奇异值。

• $\color{red}\text{Indicator function}$ : 如果 $C$ 是 convex 的， 那么它的 indicator function

\(I_C(x) = \begin{cases} 0 & x \in C \\ \infty & x \neq C \end{cases}\) 是 convex 的

• $\color{red}\text{Support function}$： 对于任何集合 $C$ (convex or not)， 它的 support function

\(I_C^*(x) = \max_{y \in C} x^\top y\) 是 convex 的

• $\color{red}\text{Max function}$： $f(x) = \max{x_1, …, x_n}$ 是 convex 的

Key properties of convex functions

• 函数是凸的，当且仅当其 restriction to any line 是 convex 的
• $\color{red}\text{Epigraph characterization}$: 函数 $f$ 是 convex 的， 当且仅当它的 epigraph

\(\text{epi}(f) = \{(x, t) \in \text{dom}(f) \times \mathbb{R} : f(x) \leq t\}\) 是 convex set

• $\color{red}\text{Convex sublevel sets}$: 如果 $f$ 是 convex 的， 那么它的 sublevel sets：

\(\{x \in \text{dom}(f) : f(x) \leq t\}\) 是 convex 的， 对于所有 $t \in \mathbb{R}$。 反之亦然。

• $\color{red}\text{First-order characterization}$： 如果 $f$ 是可微的， $f$ 是 convex 的， 当且仅当 $\text{dom}(f)$ 是 convex 的， 并且

\(f(y) \geq f(x) + \nabla f(x)^\top(y - x)\) 对所有 $x, y \in \text{dom}(f)$。 因此对于一个可微 convex function $\nabla f(x) = 0 \Leftrightarrow x \text{ minimize } f$

• $\color{red}\text{Second-order characterization}$ ： 如果 $f$ 是二阶可微的， 当且仅当 对所有 $x \in \text{dom}(f)$ , $\text{dom}(f)$ 是 convex 的 并且 $\nabla^2 f(x) \succeq 0$ ， 那么 $f$ 是 convex 的
• $\color{red}\text{Jensen’s inequality}$ ： 如果 $f$ 是 convex 的， 并且 $X$ 是一个支持 $\text{dom}(f)$ 的随机向量， 然后 $f(\mathbb{E}[X]) \leq \mathbb{E}[f(X)]$。

Operations preserving convexity

• $\color{red}\text{Nonnegative linear combination}$： $f_1, …, f_m$ 是 convex 意味着 对于任意 $a_1, …, a_m \geq 0$， $a_1 f_1 + … + a_m f_m$ 是 convex 的
• $\color{red}\text{Pointwise maximization}$： 对任意 $s \in S$， 如果 $f_s$ 是 convex 的， 那么 $f(x) = \max_{s \in S} f_s(x)$ 是 convex 的。 这里的集合 $S$ (函数 $f_s$ 的数量)是有限的
• $\color{red}\text{Partial minimization}$： 如果 $g(x, y)$ 是 convex 的， 并且 $C$ 是 convex 的， 那么 $f(x) = \min_{y \in C} g(x, y)$ 是 convex 的

Example： distances to a set

令 $C$ 是任意集合， 在一个任意范数 $| · |$下， 考虑到 $C$ 的 $\color{red}\text{maximum distance}$ ：

\(f(x) = \max_{y \in C} \| x - y \|\) 对于任意固定的 $y$, $f_y(x) = | x - y |$ 是 convex 的， 通过 pointwise maximization rule, $f$ 是 convex 的

令 $C$ 是 convex 的， 考虑到 $C$ 的 $\color{red}\text{minimum distance}$ ：

$g(x, y) = | x - y |$ 是 convex 的， 并且假设 $C$ 是 convex 的， 因此应用 partial minimization rule

More operations preserving convexity

• $\color{red}\text{Affine composition}$ ： 如果 $f$ 是 convex 的， 那么 $g(x) = f(Ax + b)$ 是 convex 的
• $\color{red}\text{General composition}$ ： 假设 $f = h \circ g$， 其中 $g : \mathbb{R}^n \rightarrow \mathbb{R}, h: \mathbb{R} \rightarrow \mathbb{R}, f: \mathbb{R}^n \rightarrow \mathbb{R}$ 那么：
• • 如果 $h$ 是 convex 并且非递减的， $g$ 是 convex 的， 那么 $f$ 是 convex 的
• • 如果 $h$ 是 convex 并且非递增的， $g$ 是 concave 的， 那么 $f$ 是 convex 的
• • 如果 $h$ 是 concave 并且非递减的， $g$ 是 concave 的， 那么 $f$ 是 concave 的
• • 如果 $h$ 是 concave 并且非递增的， $h$ 是 convex 的， 那么 $f$ 是 concave 的

如何记住这些？ 回忆当 $n = 1$ 时， 链式法则：

\(f''(x) = h''(g(x))g'(x)^2 + h'(g(x))g''(x)\)

• $\color{red}\text{Vector composition}$ ： 假设

\(f(x) = h(g(x)) = h(g_1(x), ..., g_k(x))\) 其中 $g: \mathbb{R}^n \rightarrow \mathbb{R}^k, h : \mathbb{R}^k \rightarrow \mathbb{R}, f: \mathbb{R}^n \rightarrow \mathbb{R}$， 然后

• • 如果 $h$ 是 convex 的并且在每个参数中是非递减的， $g$ 是 convex 的， 那么 $f$ 是 convex 的
• • 如果 $h$ 是 convex 的并且在每个参数中是非递增的， $g$ 是 concave 的， 那么 $f$ 是 convex 的
• • 如果 $h$ 是 concave 的并且在每个参数中是非递减的， $g$ 是 concave 的， 那么 $f$ 是 concave 的
• • 如果 $h$ 是 concave 的并且在每个参数中是非递增的， $g$ 是 convex 的， 那么 $f$ 是 concave 的

Example： log-sum-exp function

$\color{red}\text{Log-sum-exp function}$： 对于固定的 $a_i, b_i, i = 1, …, k$， $g(x) = \log(\sum_{i=1}^k e^{a_i^\top x + b_i})$ 。 通常叫做 “soft max” , 因为它估计 $\max_{i=1, …, k}(a_i^\top x + b_i)$

首先， 足够证明 $f(x) = \log (\sum_{i=1}^n e^{x_i})$ 的 convexity (affine composition rule)

现在使用使用 second-order characterization。 计算：

\(\nabla_i f(x) = \frac{e^{x_i}}{\sum_{\ell = 1}^n e^{x_\ell}}\) \(\nabla_{ij}^2 f(x) = \frac{e^{x_i}}{\sum_{\ell = 1}^n e^{x_\ell}} 1\{i = j\} - \frac{e^{x_i}e^{x_j}}{(\sum_{\ell=1}^n e^{x_\ell})^2}\)

将 $\nabla^2 f(x) = \text{diag}(z) - zz^\top$， 其中 $z_i = e^{x_i} / (\sum_{\ell = 1}^n e^{x_\ell})$。 这个矩阵是主对角矩阵， 因此是半正定的。

• Previous
  【深度学习】USR-DU：Learning Degradation Uncertainty for Unsupervised Real-world Image Super-resolution
• Next
  【机器学习】Proximal Gradient Descent