Optimization terminology

一个凸优化问题是：

$\max_{x \in D} f(x) \quad \text{subject to} \quad g_i(x) \leq 0, i = 1, ..., m \quad Ax=b$ 其中 $f$ 和 $g_i, i = 1, …, m$ 全是 convex 的，并且 optimization domain 是 $D = \text{dom}(f) \cap \bigcap_{i=1}^m dom(g_i)$

$f$ 叫做 $\color{red}\text{criterion}$ 或者 $\color{red}\text{objective}$ 函数
$g_i$ 叫做 $\color{red}\text{inequality constraint}$ 函数
如果 $x \in D, g_i(x) \leq 0, i = 1, …, m$，并且 $Ax = b$，那么 $x$ 叫做 $\color{red}\text{feasible point}$
对所有 feasible points $f(x)$ 的 $f(x)$ 的最小值叫做 $\color{red}\text{optimal value}$，写作 $f^*$
如果 $x$ 是 feasible 的并且 $f(x) = f^*$，那么 $x$ 叫做 $\color{red}\text{optimal}$; 也叫做一个 $\color{red}\text{solution}$ 或者 $\color{red}\text{minimizer}$
如果 $x$ 是 feasible 的并且 $f(x) \leq f^* + \epsilon$，那么 $x$ 叫做 $\color{red}\epsilon\text{-subotimal}$
如果 $x$ 是 feasible 的并且 $g_i(x) = 0$，那么 $g_i$ 在 $x$ 是 $\color{red}\text{active}$ 的
凸最小化可以作为凹(concave)最大化来定位

\[\min_x f(x) \quad \text{subject to} \quad g_i(x) \leq 0 i=1, ..., m \quad Ax=b \quad i=1, ..., m \quad Ax = b \\ \Leftrightarrow \max_x -f(x) \quad \text{subject to} \quad g_i(x) \leq 0 \quad i=1, ..., m \quad Ax = b\]

两者都是凸优化问题

Solution set

令 $X_{opt}$ 表示凸问题的所有解的集合，写作：

$X_{opt} = \text{argmin} \quad f(x) \quad \text{subject to} \quad g_i(x) \leq 0, i = 1, ..., m \quad Ax = b$ Key property 1: $X_{opt}$ 是一个 $\color{red}\text{convex set}$

证明：如果 $x, y$ 是解，那么对于 $0 \leq t \leq 1$

$g_i(tx + (1 - t)y) \leq tg_i(x) + (1 - t) g_i(y) \leq 0$
$A(tx + (1 - t)y) = tAx + (1 - t)Ay = b$
$f(tx + (1 - t)y) \leq tf(x) + (1 - t)f(y) = f^*$

因此 $tx + (1 - t)y$ 也是一个解

Key proberty 2: 如果 $f$ 是 strictly convex，那么 $\color{red}\text{solution is unique}$，如， $X_{opt}$ 包含一个元素。

Example： lasso

给定 $y \in \mathbb{R}^n, X \in \mathbb{R}^{n \times p}$， $\color{red}\text{lasso}$ problem：

$\min_\beta \|y - X \beta\|_2^2 \quad \text{subject to} \quad \|\beta\|_1 \leq s$ 它是 convex 的吗？它的 criterion 函数是什么？ inequality 和 equality constraints 是什么？可行解集是什么？如果解唯一，当：

$n \geq p$ 并且 $X$ 是列满秩矩阵吗？
$p > n$ 吗？

如果我们将 criterion 变为 $\color{red}\text{Huber loss}$，我们的答案会发生什么变化？

$\sum_{i=1}^n \rho(y_i - x_i^\top \beta), \rho(z) = \begin{cases} \frac{1}{2} z^2 & \mid z \mid \leq \delta \\ \delta \mid z \mid - \frac{1}{2} \delta^2 & \text{else} \end{cases}$

Example： support vector machines

给定 $y \in {-1, 1}^n, X \in \mathbb{R}^{n \times p}$ , 行为 $x_1, …, x_n$，考虑 $\color{red}\text{support vector machine}$ 或 SVM 问题：

\[\min_{\beta, \beta_0, \xi} \frac{1}{2}\|\beta\|_2^2 + C \sum_{i=1}^n \xi_i \quad \text{subject to} \quad \xi_i \geq 0, \quad i = 1, ..., n \\ y_i(x_i^\top \beta + \beta_0) \geq 1 - \xi_i, i = 1,..., n\]

它是 convex 的吗？它的 criterion 函数是什么？约束和可行解集是什么？解 $\beta, \beta_0, \xi$ 唯一吗？如果将 criterion 变为下式会怎样：

\[\frac{1}{2} \|\beta\|_2^2 + \frac{1}{2} \beta_0^2 + C \sum_{i=1}^n \xi_i^{1.01}\]

Local minima are global minima

对于一个 convex problem，一个 feasible point $x$ 叫做 $\color{red} \text{locally optimal}$, 局部最优是指 $R > 0$，有：

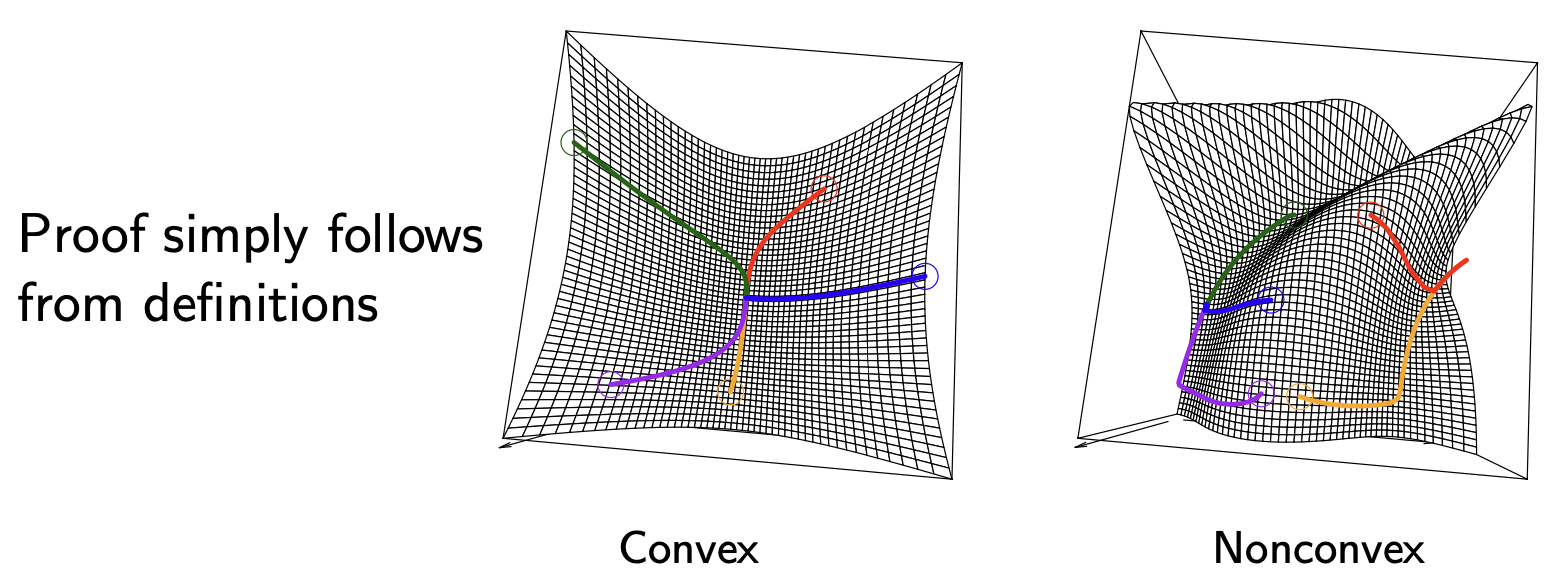
\[f(x) < f(y) \quad \text{for all feasible $y$ such taht} \quad \|x - y\|_2 \leq R\]

对于凸优化问题， $\color{red}\text{local optima are global optima}$。

Rewriting constraints

优化问题：

$\min_x f(x) \quad \text{subject to} \quad g_i(x) \leq 0, i=1,..., m \quad Ax = b$ 其可以写作：

\[\min_x f(x) \quad \text{subject to} \quad x \in C\]

其中可行解集为 $C = {x : g_i(x) \leq 0, i = 1, …, m, Ax = b}$。因此，后一种表述是 $\color{red}\text{compelely general}$

使用 $I_C$ 作为C的 indicator，我们可以以无约束的形式写入：

\[\min_x f(x) + I_C(x)\]

First-order optimality condition

对于一个 convex problem：

\[\min_x f(x) \quad \text{subject to} \quad x \in C\]

和可微的 $f$ ，当且仅当下式成立的时候，一个 feasible point $x$ 是 optimal 的

\[\nabla f(x)^T (y - x) \geq 0 \quad \text{for all} \quad y \in C\]

这叫作 $\color{red}\text{first-order condition for optimality}$

简单来说， $x$ 可行的方向与梯度 $\nabla f(x)$ 对齐

重要的特殊情况: 如果 $C = \mathbb{R}^n$(无约束优化)，那么 optimality condition 退化为 $\nabla f(x) = 0$

Example: quadratic minimization

考虑最小化 $\color{red}\text{quadratic function}$

$f(x) = \frac{1}{2}x^\top Q x + b^\top x + c$ 其中 $Q \succeq 0$。 first-order condition 表明解满足：

$\nabla f(x) = Qx + b = 0$

如果 $Q \succ 0$, 那么存在唯一解 $x = -Q^{-1}b$
如果 $Q$ 是 singular 并且 $b \notin \text{col}(Q)$，那么无解(例如 $\min_x f(x) = -\infty$)
如果 $Q$ 是 singular 并且 $b \in \text{col}(Q)$，那么存在无穷多解：

$x = -Q^+b + z, \quad z \in \text{null}(Q)$ 其中 $Q^+$ 是 $Q$ 的 $\color{red}\text{pseudoinverse}$

【机器学习】Convexity II: Optimization Basics