Abstract
近年来在视觉的自注意力和纯多层感知器(MLP)模型方面取得的进展显示出在减少归纳偏置的情况下实现有前景的性能方面的巨大潜力。
这些模型通常基于从原始数据中学习空间位置之间的相互作用。
这篇文章提出了一种概念上简单但计算效率高的全局滤波网络(GFNet),它学习频率域内具有对数线性复杂度的长程空间相关性。
该架构用三个关键操作取代了视觉 Transformer 中的自注意层:二维离散傅里叶变换、频域特征和可学习的 global filter 之间的元素相乘,以及二维傅里叶反变换。
作者同时在 ImageNet 和 下游任务上展示了模型可喜的 准确率/复杂度权衡
Method
Global Filter Networks
Overall architecture. 视觉 Transformer 的最新进展[10,43]表明,即使没有与卷积相关的归纳偏置,基于自注意力的模型也可以实现竞争性能。 此后,有几部工作[42,41]利用了除自注意力以外的方法(如MLPs)在 tokens 之间混合信息。提出的 Global Filter Networks (GFNet)遵循这一工作路线,旨在用更简单、更高效的自注意层取代计算度复杂(($O(N^2)$))的自注意力层。
模型的总体架构如图1所示。模型的输入为 $H \times W$ 的不重叠的 patches 并且将拉平的 patches 沿着维度 $D$ 投影为 $L = HW$ 的 tokens。 GFNet 的基本块包括:
- global filter layer: 其高效地交换空间信息 ($O(L \log L)$)
- feedforward network(FFN)
最后一个 block 的输出 token 被送入一个全局平均池化层,后面跟着一个线性分类器。
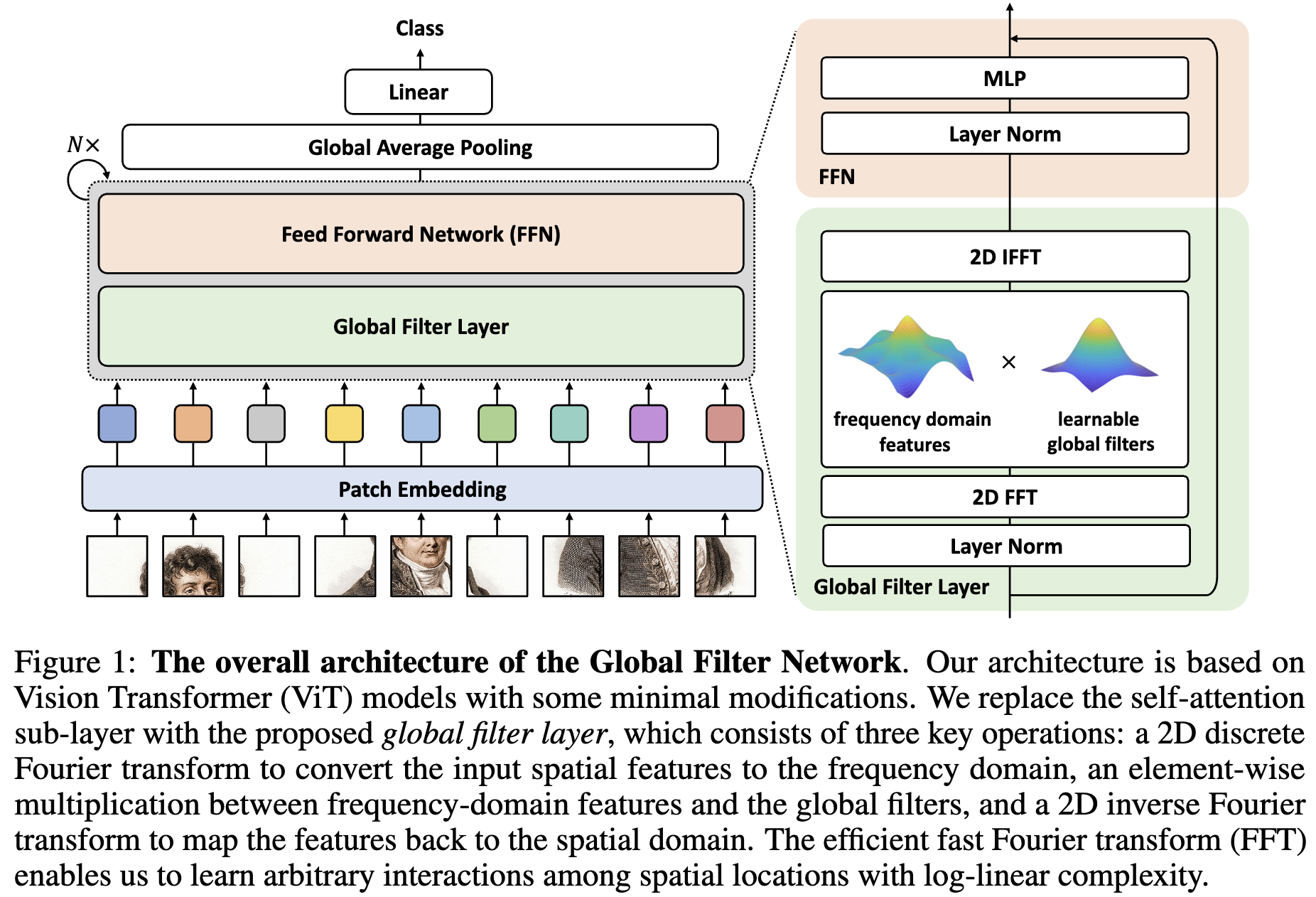
Global filter layer. 作者提出 global filter 层作为自注意力层的替代,它可以混合表示不同空间位置的 token。给定 tokens $x \in \mathbb{R}^{H \times W \times D}$, 首先沿着空间维度执行 2D FFT 将 $x$ 转换到频率域:
\[X = \mathcal{F}[x] \in \mathbb{C}^{H \times W \times D}\]$X$ 是复数张量并且表示 $x$ 的 spectrum。 通过将可学习的 filter $K \in \mathbb{C}^{H \times W \times D}$ 与 $X$ 相乘调制 spectrum。
\[\tilde X = K \odot X\]filter $K$ 与 $X$ 具有相同的维数,可以表示频域中任意的 filter ,因此称为 global filter。最后,采用 FFT 反变换将调制后 spectrum $\tilde X$ 变换回空间域并更新 token。
\[x \leftarrow \mathcal{F}^{-1}[\tilde X]\]作者还发现,虽然提出的 global filter 也可以解释为空间域操作,但在网络中学习的 filter 在频域比空间域表现出更清晰的模式,这表明模型倾向于捕捉频域而不是空间域的关系(见图4)。

注意,在频域实现的 global filter 也比在空间域实现的高效得多,频率域的复杂度 $O(DL \log L)$, 空间域中原始的 depthwise global circular convolution 的计算复杂度为 $O(DL^2)$。
Conclusion
这篇文章提出了 Global Filter Network(GFNet), 其实一个简单但是计算高效的结构。
该模型将视觉 Transformer 自注意力子层替换为 2D FFT/IFFT 和一组可学习的 global filters。
得益于对数线性复杂度的 token mixing操作,该架构是高效的。
-
Previous
【深度学习】A New TwIST: Two-Step Iterative Shrinkage Thresholding Algorithms for Image Restoration -
Next
【深度学习】DeSCI:Rank Minimization for Snapshot Compressive Imaging