Abstract

目标检测标签分配的最新进展主要寻求为每个真实目标定义正/负训练样本。

这篇文章从全局角度创新地重新审视了标签分配，并提出将分配过程表述为最优传输（OT）问题——这是优化理论中一个经过充分研究的课题。

具体而言，我们将每个先验框(demander)和真实标签(supplier)对之间的单位运输成本定义为其分类和回归损失的加权和。

制定后，找到最佳分配解决方案，以最低的传输成本解决最佳传输计划，这可以通过Sinkhorn-Knopp迭代解决。

在COCO上，一个配备最佳传输分配(OTA)的FCOS-ResNet-50检测器可以在 1× scheduler 下达到40.7%的mAP，优于所有其他现有分配方法。

Method

在这节中，作者首先回顾了了最优传输问题的定义，然后演示了如何将目标检测中的标签分配转化成OT问题。作者还介绍了两种先进的设计，建议采用这两种设计来充分利用OTA。

Optimal Transport

最佳运输（OT）描述了以下问题：假设某个领域有 $m$ 个供应商和 $n$ 个需求者。第 $i$ 个供应商有 $s_i$ 个货物，而第 $j$ 个需求者需要 $d_j$ 个货物。从第 $i$ 个供应商到第 $j$ 个需求者的每个货物的传输代价为 $c_{ij}$。 OT 问题的目标是找到一个传输方案 $\pi^* = {\pi_{i, j} \mid i = 1, 2, …, m, j = 1, 2, …, n}$，根据该方法，供应商的所有货物都可以以最低的运输成本转运给需求者：

\[\min_\pi \sum_{i=1}^m \sum_{j=1}^n c_{ij} \pi_{ij} \\ s.t. \sum_{i=1}^m \pi_{ij} = d_j, \quad \sum_{j=1}^n \pi_{ij} = s_i, \\ \sum_{i=1}^m s_i = \sum_{j=1}^n d_j, \\ \pi_{ij} \geq 0, i = 1, 2, ..., m, j = 1, 2, ..., n \tag{1}\]

这是一个可以在多项式时间内求解的线性程序。然而，由此产生的线性程序是巨大的，涉及特征维度的平方。因此，作者通过一个名为Sinkhorn-Knopp[5]的快速迭代解决方案来解决这个问题。

OT for Label Assignment

在目标检测中，假设对于输入图像 $I$ 存在 $m$ 个真实目标和 $n$ 个先验框(在所有 FPN 层级上)，作者将每个真实标签视为带有 $k$ 个正标签的供应商(例如 $s_i=k, i = 1, 2, …, m$)，并且每个先验框视为一个需求者，其需要一个标签(例如 $d_j=1, j=1, 2, …, n$)。将一个正标签从 $gt_i$ 到先验框 $a_j$ 的代价被定义为它们的 $cls$ 和 $reg$ 损失之和：

\[c_{ij}^{fg} = L_{cls}(P_j^{cls}(\theta)， G_i^{cls}) \\ + \alpha L_{reg}(P_j^{box}(\theta), G_i^{box}) \tag{2}\]

其中 $\theta$ 表示模型参数。 $P^{cls}j$ 和 $P_j^{box}$ 表示对 $a_j$ 预测的 $cls$ 分数和边界框。 $G_i^{cls}$ 和 $G_i^{box}$ 表示 $gt_i$ 的真实类别和边界框。 $L{cls}$ 和 $L_{reg}$ 表示交叉熵损失和 IoU 损失。人们也可以用Focal loss 和 GIoU/Smooth L1 loss 取代这两种损失。$\alpha$ 是平衡系数。

除了正分配外，在训练期间，大量先验框也被视为负样本。由于最优运输涉及所有先验框，我们引入了另一个供应商-背景，他们只提供负标签。在标准OT问题中，总供应量必须等于总需求。因此，我们将背景可以提供的负标签数量设置为 $n − m \times k$。将一个单位负标签从背景运输到 $a_j$ 的成本定义为：

$c_j^{bg} = L_{cls}(P_j^{cls}(\theta), \emptyset) \tag{3}$ 其中 $\emptyset$ 表示背景类。拼接 $c^{bg} \in \mathbb{R}^{1 \times n}$ 到 $c^{fg} \in \mathbb{R}^{m \times n}$最后一行，可以得到代价矩阵 $c \in \mathbb{R}^{(m + 1) \times n}$ 的闭式解。供应向量 $s$ 应该相应地按如下更新：

\[s_i = \begin{cases} k, \quad if \quad i \leq m \\ n - m \times k， \quad if \quad i = m + 1 \end{cases} \tag{4}\]

因为我们已经有了代价矩阵 $c$，供应向量 $s \in \mathbb{R}^{m+1}$ 和需求向量 $d \in \mathbb{R}^n$, 最优传输策略 $\pi^* \in \mathbb{R}^{(m+1) \times n}$ 可以通过使用 Sinkhorn-Knopp 迭代求解这个 OP 问题得到。在得到 $\pi^*$ 之后，可以解码相应的标签分配策略，通过分配每个先验框到供应商，供应商传出最大数量的标签给他们。后续过程(例如基于分配结果的计算，反向传播)与 FCOS 和 ATSS 相同。注意到 OT 问题的优化过程仅包含一些矩阵乘法，这些乘法可以由GPU设备加速，因此 OTA 只会将总训练时间增加不到20%，并且在测试阶段完全免费。

Advanced Designs

Center Prior. 以前的工作只从具有边缘区域的物体的中心区域中选择正先验框，称为 Center Prior。这是因为他们要么在随后的过程中有大量模棱两可的先验框，要么有糟糕的统计数据。OTA不是依赖统计特征，而是基于全局优化方法，因此自然而然地克服了这两个问题。从理论上讲，OTA 可以将真是边界框区域内的任何先验框分配为正样本。然而，对于COCO等一般检测数据集，作者发现 Center Prior 仍然受益于OTA的训练。强迫检测器专注于潜在的正区域（即中心区域）有助于稳定训练过程，特别是在训练的早期阶段，这将导致更好的最终表现。因此，作者在代价矩阵之前施加一个 Center Prior。对于每个gt，根据先验框和 gts 之间的中心距离从每个 FPN 层级中选择 $r^2$ 最近的先验框。至于不在 $r^2$ 最接近列表中的先验框，它们在代价矩阵 $c$ 中的相应条目将受到额外常数成本的影响，以减少它们在训练阶段被分配为正样本的可能性。在第4部分，作者展示了尽管OTA像其他工作[38、47、48]一样采用一定程度的中心先验，但当r设置为大值时，OTA一直以很大的优势优于对手(例如大量潜在的正先验框以及模棱两可的先验框)。

Dynamic k Estimation. 直觉上，每个 gt（即 Sec3.1 中的 $s_i$ ）的适当正先验框数量应该不同，并基于许多因素，如物体的大小、比例和遮挡条件等。由于很难直接建模从这些因素到正先验框数量的映射函数，作者提出了一种简单而有效的方法，根据预测边界框和 gt 之间的IoU值粗略估计每个 gt 的适当数量。具体来说，对于每个gt，根据 IoU 值选择最大的 $q$ 个预测。这些 IoU 值的总和表示此 gt 的估计正先验框数量。作者将此方法命名为动态 $k$ 估计。这种估计方法基于以下直觉：特定 gt 的适当数量的正先验框应与回归此 gt 的先验框数量呈正相关。在第4节中，作者详细比较了固定 $k$ 和动态 $k$ 估计策略。

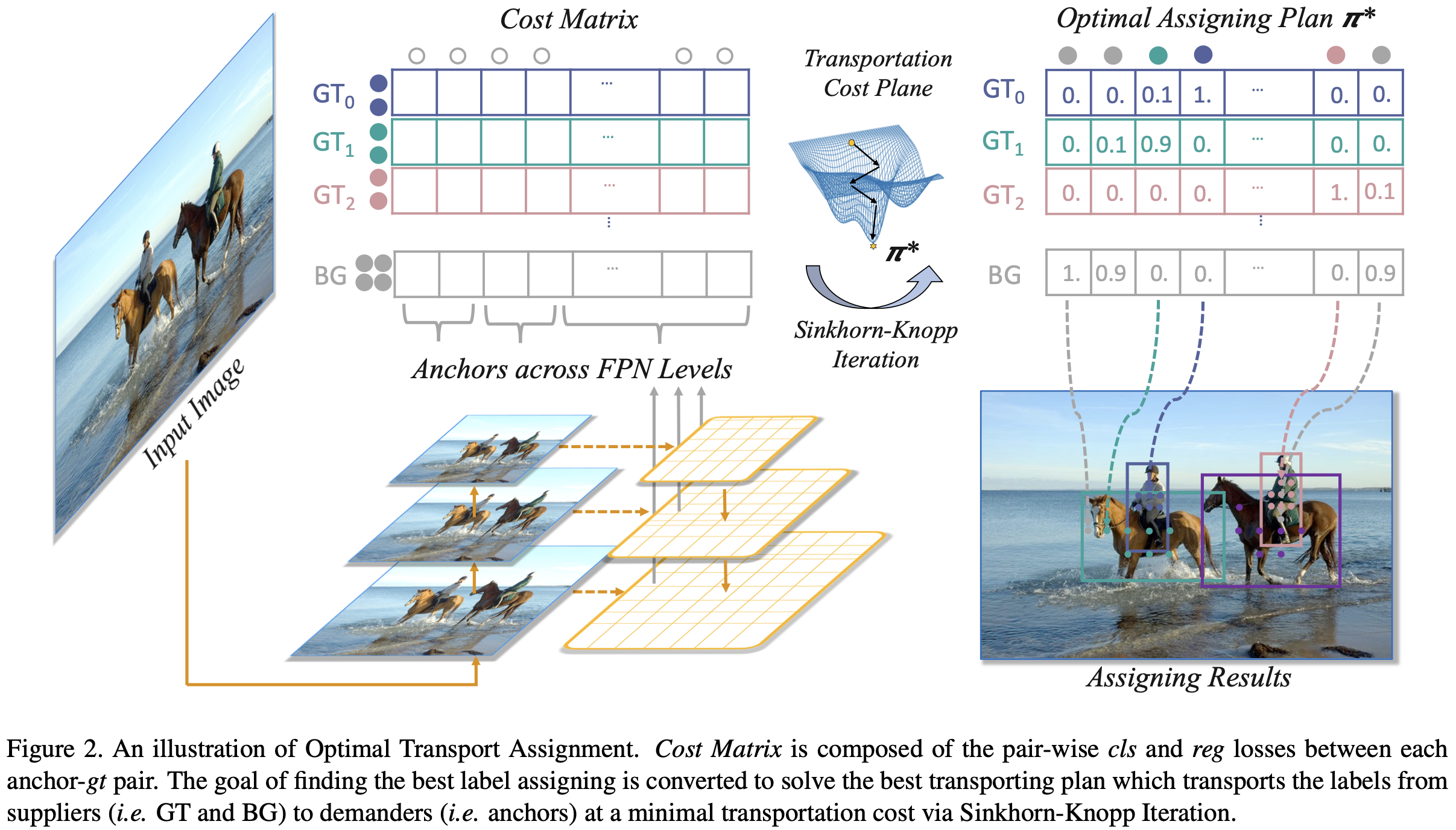
OTA的可视化如图2所示。作者还描述了 OTA 完整的过程，包括算法1中的中心先验和动态 $k$ 估计。

Conclusion

这篇文章提出了一种基于优化理论的标签分配策略——最优传输分配。

OTA将目标检测中的标签分配程序设计为最佳传输问题，该问题旨在以最低的传输成本将标签从真实目标和背景传输到先验框。

为了确定每个真是标签所需的正标签数量，坐着进一步根据预测边界框和每个真实标签之间的IoU值提出一个简单的估计策略。

如实验所示，OTA 在 MS COCO 上实现了新的SOTA性能。

由于OTA可以很好地处理模棱两可的先验框的分配，它还比CrowdHuman数据集中的所有其他单阶段检测器优异，这表明其强大的泛化能力。

【深度学习】OTA: Optimal Transport Assignment for Object Detection

Abstract

Method

Optimal Transport

OT for Label Assignment

Advanced Designs

Conclusion

CATALOG

FEATURED TAGS

FRIENDS