Abstract

由于其构建模块中的固定几何结构，卷积神经网络（CNN）本质上仅限于模拟几何变换。

在这项工作中，作者引入了两个新模块，以提高 CNN 的变换建模能力，即 deformable convolution 和 deformable RoI pooling。

两者都基于使用额外的偏移量来增强模块中的空间采样位置的想法，并在没有额外监督的情况下从目标任务中学习偏移量。

新模块可以很容易地取代现有CNN中的普通模块，并且可以通过标准反向传播轻松端到端训练，从而产生可变形的卷积网络。

大量的实验证明方法的性能。

这篇文章首次表明，在深度CNN中学习密集的空间变换对目标检测和语义语义分割等复杂的视觉任务是有效的。

Deformable Convolutional Networks

CNN中的特征图和卷积是3D的。deformable convolution 和 RoI pooling 模块都在二维空间域上运行。在整个通道维度上，操作保持不变。为了清晰的符号清晰起见，这些模块在这里以2D描述。扩展到3D很简单。

2D 卷积包括两个步骤：

1) 对输入特征图 $x$ 使用网格 $\mathcal{R}$ 采样；

2）采样值被 $w$ 加权求和

网格 $\mathcal{R}$ 定义为 receptive field size 和 dilation。

对于在输出特征图 $y$ 的每个位置 $p_0$，有：

$y(p_0) = \sum_{p_n \in \mathcal{R}} w(p_n) · x(p_0 + p_n)$ 其中 $p_n$ 是 $\mathcal{R}$ 的位置枚举。

在 deformable convolution 中，网格 $\mathcal{R}$ 由偏移量 ${\Delta p_n \mid n = 1, …, N}$，其中 $N = \mid R \mid$ 增强, 上式变为：

\[y(p_0) = \sum_{p_n \in \mathcal{R}} w(p_n) · x(p_0 + p_n + \Delta p_n)\]

现在，采样在带有偏移量的位置 $p_n + \Delta p_n$上进行。偏移量 $\Delta p_n$ 通常很小，上式通过双线性插值实现：

$x(p) = \sum_q G(q, p) · x(q)$ 其中 $p$ 表示任意的位置 $p = p_0 + p_n + \Delta p_n$， $q$ 枚举特征图 $x$ 的所有内部空间位置， $G(·，·)$ 是双线性插值核。注意$G$ 有两个维度。它被分为两个一维核：

\[G(q, p) = g(q_x, p_x) · g(q_y, p_y)\]

其中 $g(a, b) = \max(0, 1 - \mid a - b \mid)$。

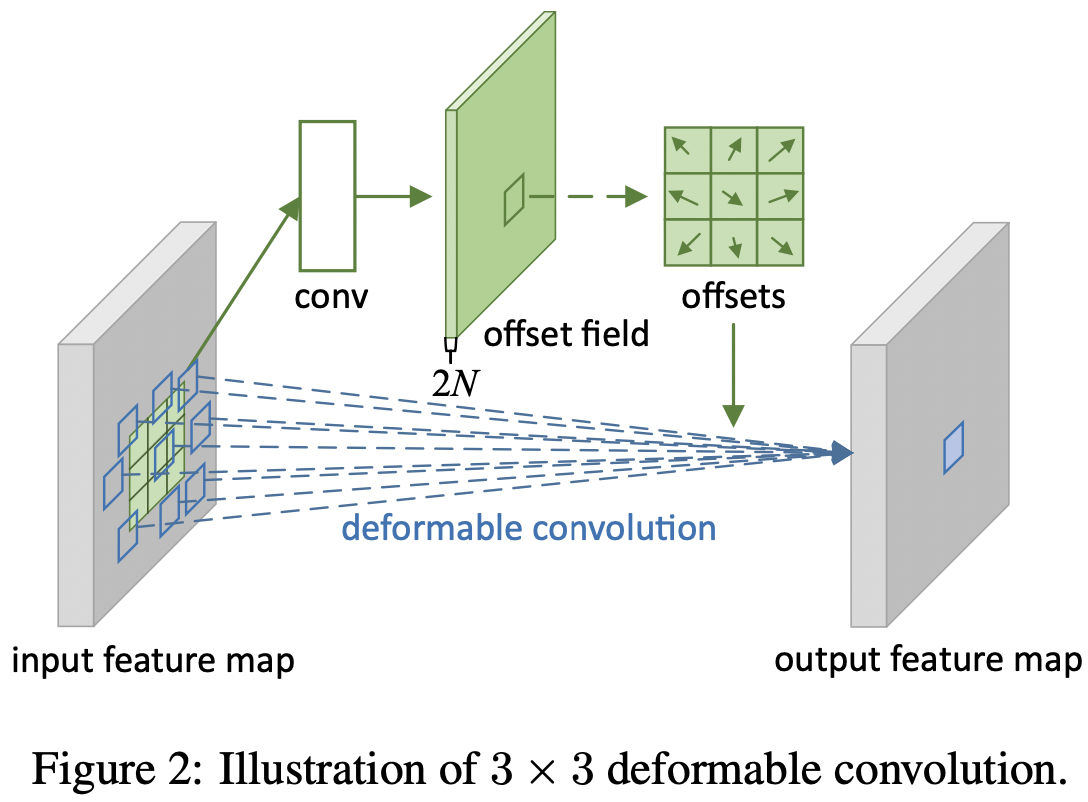
如图2所示，偏移量通过在所有输入特征图上应用卷积层得到。卷积核与现有的卷积层相同的空间分辨率和扩张。输出 offset fields 有和输入特征图相同的空间分辨率。通道维度 $2N$ 对应于 $N$ 个 2D 偏移量。在训练期间，同时学习用于生成输出特征的卷积核和偏移量。

本文提出了 deformable ConvNets，这是一种简单、高效、深度和端到端的解决方案，用于模拟密集的空间变换。

第一次，作者证明了在 CNN 中学习密集的空间转换是可行和有效的，用于复杂的视觉任务，如目标检测和语义分割。