Abstract
几年来,基于先验框的检测器一直主导目标检测。
最近,由于 FPN 和 Focal Loss 的提出,无先验框的检测器变得流行起来。
在这篇文章中,作者首先指出,基于先验框的检测和无先验框检测之间的差异实际上是如何定义正负训练样本,这导致它们之间的性能差距。
如果它们在训练期间对正负样本采用相同的定义,那么无论从边界框还是从点回归,最终表现都不会有任何明显的差异。
这表明,如何选择正负训练样本对当前物体检测器很重要。
然后,作者提出了一个自适应训练样本选择(ATSS),根据目标的统计特征自动选择正负样本。
它显著改善了基于先验框和无先验框检测器的表现,并减少了了它们之间的差距。
最后,作者讨论了在图像上每个位置平铺多个先验框以检测物体的必然性。
Adaptive Training Sample Selection
在训练目标检测器时,首先需要定义正负样本进行分类,然后使用正样本进行回归。根据之前的分析,前者至关重要,无先验框检测器 FCOS 改进了这一步骤。它引入了一种定义正负样本的新方法,与传统的基于 IoU 的策略相比,它实现了更好的性能。受此启发,作者深入研究了目标检测中最基本的问题:如何定义正负训练样本,并提出自适应训练样本选择(ATSS)。与这些传统策略相比,该方法几乎没有超参数,并且对不同的设置很强大。
Description
之前的样本选择策略有一些敏感的超参数,例如基于先验框的检测器中的 IoU 阈值和无先验框检测器中的缩放范围。设置这些超参数后,所有真实边界框都必须根据固定规则选择其正样本,这些规则适用于大多数目标,但一些其他目标会被忽略。因此,这些超参数的不同设置将产生非常不同的结果。
为此,作者提出了ATSS方法,该方法根据物体的统计特征自动划分正样本和负样本,几乎无需任何超参数。算法1描述了该方法如何适用于输入图像。对于图像上的每个真实边界框 $g$ ,首先找到其候选正样本。如第 3 行至第 6 行所述,在每个金字塔层,作者根据 L2 距离选择中心最接近 $g$ 中心的 $k$ 个先验框。假设有 L 层特征金字塔,真实边界框 $g$ 将有 $k \times L$ 个候选正样本。之后,作者将这些候选者之间的 IoU 和第7行的真实边界框 $g$ 计算为 $D_g$,其均值和标准差在第8行和第9行中计算为 $m_g$ 和 $v_g$。通过这些统计数据,这个真实边界框 $g$的 IoU 阈值通过第十行的 $tg = m_g + v_g$ 得到。最后, 作者选择这些大于等于 IoU 阈值的候选者作为正样本, 如第11行到第15行。值得注意的是,我们还将正样本的中心限制在真实边界框中,如第12行所示。此外,如果将先验框分配给多个真实边界框,将选择 IoU 最高的边界框。其余是负样本。该方法背后的一些动机解释如下。

Selecting candidates based on the center distance be- tween anchor box and object. 对于 RetinaNet,当先验框的中心更靠近物体中心时,IoU会更大。对于FCOS,靠近物体中心的先验点将产生更高质量的检测。因此,离物体中心越近的先验框/点就越好。
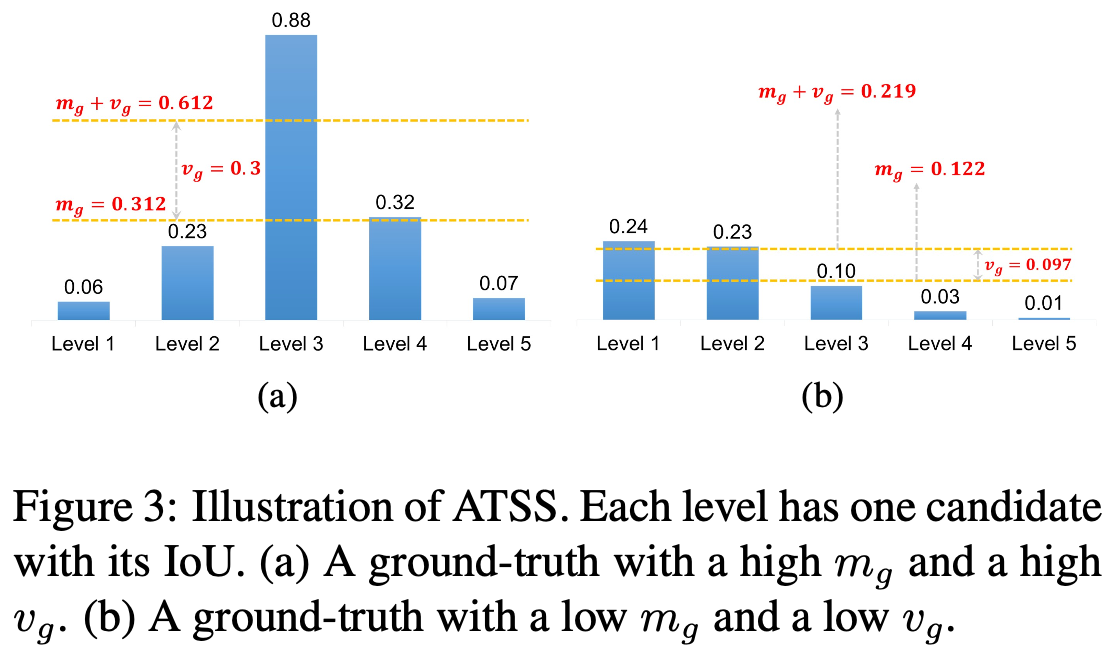
Using the sum of mean and standard deviation as the IoU threshold. 目标的 IoU 均值 $m_g$ 是衡量预设先验对该目标适用性的指标。一个高的 $m_g$ 如图3(a) 所示表明它有高质量的候选者。如图3(b)所示,低 $m_g$ 表明,其大多数候选者质量低,IoU 阈值应较低。此外,目标的 IoU 标准差 $v_g$ 是衡量哪些层适合检测该目标的指标。如图3(a)所示,高 $v_g$ 意味着有一个专门适合该目标的金字塔层级,将 $v_g$ 加上 $m_g$ 可以获得一个高阈值,仅从该层级中选择正样本。如图3(b)所示,低 $v_g$ 表示有几个金字塔层级适合此目标,将 $v_g$ 加上 $m_g$ 可以获得从这些层级中选择合适的正样本的低阈值。使用均值 $m_g$ 和标准差 $v_g$ 的和作为IoU阈值 $t_g$,可以根据物体的统计特征,从适当的金字塔层级自适应地为每个目标选择足够的正样本。
Conclusion
在这项工作中,作者指出,单阶段先验框检测器和基于中心的无先验检测器之间的本质区别实际上是正负训练样本的定义。
它表明,如何在目标检测训练期间选择正负样本至关重要。
受此启发,作者深入研究了这个基本问题,并提出了自适应训练样本选择,该选择根据目标的统计特征自动划分正负训练样本,从而减少了基于先验框和无先验框检测器之间的差距。
作者还讨论了在每个位置平铺多个先验框的必要性,并表明在当前情况下,这可能不是那么有用的操作。