Abstract
机器学习的一个核心问题涉及使用高度灵活的概率分布对复杂的数据集进行建模,其中学习、采样、推理和评估在分析或计算上仍然可以处理。
在这里,作者开发了一种同时实现灵活性和可操作性的方法。
受非平衡统计物理学的启发,本质思想是通过迭代正向扩散过程系统地缓慢地破坏数据分布中的结构。
然后,作者学习了一个反向扩散过程,该过程恢复了数据中的结构,产生了一个高度灵活和易于处理的数据生成模型。
这种方法能够快速学习、采样和评估具有数千层或时间步骤的深度生成模型中的概率,并在学习好的模型下计算条件概率和后验概率。
Algorithm
作者的目标是定义一个正向(或推理)扩散过程,将任何复杂的数据分布转换为简单、可操作的分布,然后学习这个扩散过程的有限时间步的逆过程,该扩散过程定义了生成模型分布(见图1)。作者首先描述了正向推理扩散过程。然后,作者展示了如何训练反向生成扩散过程并用于评估概率。作者还推导了反向过程的熵界限,并展示了如何将学习分布乘以任何第二个分布(在 inpainting 或去噪图像时计算后验会做的那样)。
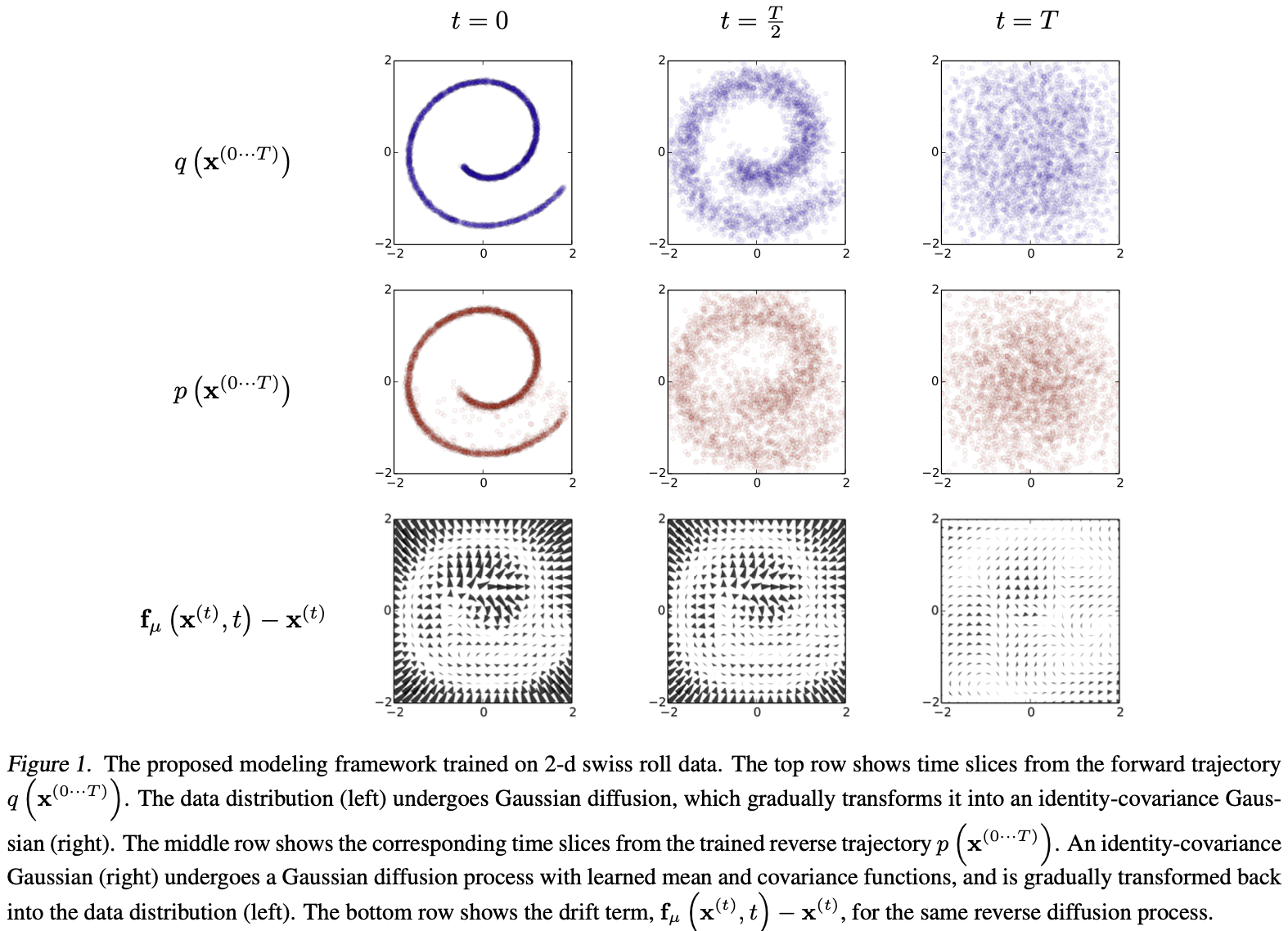
Forward Trajectory
首先标记数据分布 $q(x^{(0)})$。 数据分布逐渐转换为一个表现良好的分布 $\pi(y)$,通过对重复应用马尔科夫扩散核 $T_\pi(y \mid y’; \beta)$ , 其中 $\beta$ 是扩散率。
\[\pi(y) = \int dy' T_\pi(y \mid y'; \beta) \pi(y') \tag{1}\]\(q(x^{(t)} \mid x^{(t-1)}) = T_\pi(x^{(t)} \mid x^{(t-1)}; \beta_t) \tag{2}\) 前向过程从开始的数据分布执行 $T$ 步扩散, 有:
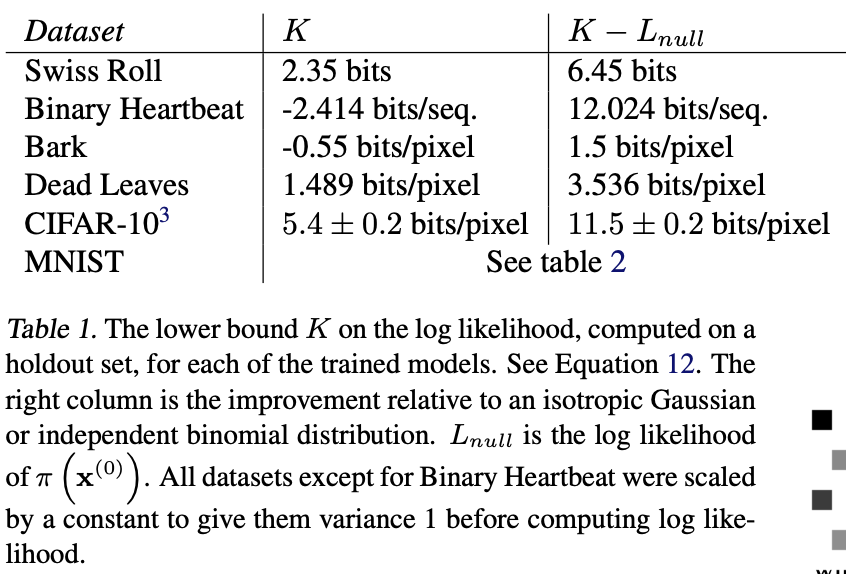
\[q(x^{(0, ..., T)}) = q(x^{(0)}) \prod_{t=1}^T q(x^{(t)} \mid x^{(t-1)}) \tag{3}\]对于下面展示的实验, $q(x^{(t)} \mid x^{(t-1)})$ 对应于高斯扩散到具有单位协方差的高斯分布,或二项扩散到独立的二项分布。表1 给出了高斯分布和二项分布的扩散核。
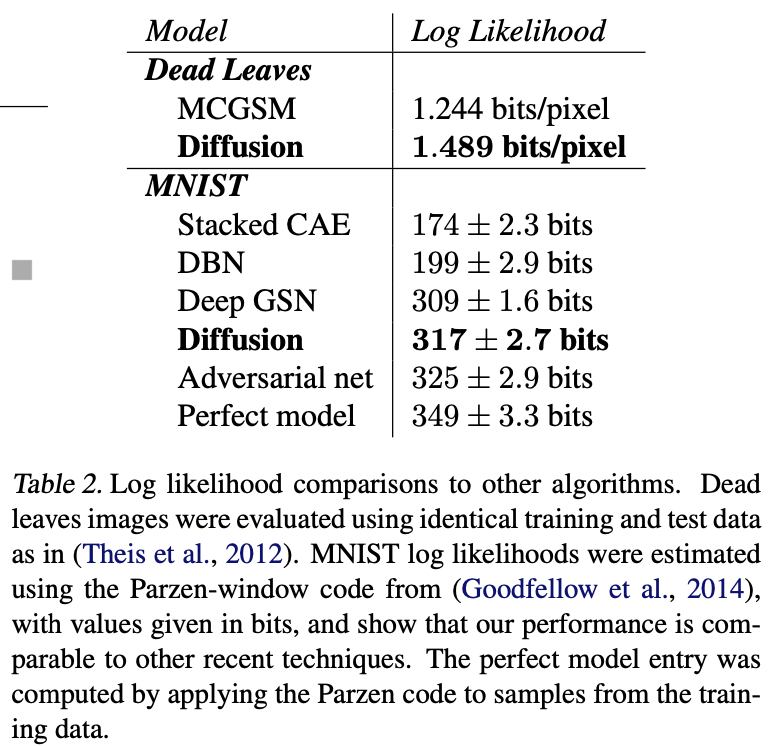
Reverse Trajectory
生成分布将被训练来描述相反的过程
\(p(x^{(T)}) = \pi(x^{(T)}) \tag{4}\) \(p(x^{(0 ... T)}) = p(x^{(T)}) \prod_{t=1}^T p(x^{(t-1)} \mid x^{(t)}) \tag{5}\)
对于高斯扩散和二项扩散,对于连续扩散(限制小步长$\beta$),扩散过程的逆过程具有与正向过程相同的函数形式。因为 $q(x^{(t) \mid x^{(t-1)}})$ 是一个小的高斯(二项)分布,如果 $\beta_t$ 很小, 那么 $q(x^{(t-1) \mid x^{(t)}})$ 将也是一个高斯(二项)分布。扩散的步数越多, 扩散率 $\beta$ 可以越小。
在学习期间,只需要估计高斯扩散核的平均值和协方差,或二项核的 bit flip 概率。如表1所示, $f_\mu(x^{(t), t})$ 和 $f_\Sigma(x^{(t)}, t)$ 是定义逆马尔科夫转移过程的均值和协方差的函数, $f_b(x^{(t)}, t)$ 是提供二项分布提供 bit flip 概率的函数。 运行此算法的计算成本是这些函数的成本,乘以时间步数。对于这篇文章的所有结果,使用多层感知器来定义这些函数。然而,将适用于广泛的回归或函数拟合技术,包括非参数方法。
Model Probability
生成模型分配给数据的概率是:
\(p(x^{(0)}) = \int dx^{(1...T)} p(x^{(0...T)}) \tag{6}\) 这个积分是不可追溯的 —— 但从退火的重要性采样和Jarzynski等式中得到了暗示,作者评估了正向和反向轨迹的相对概率,在正向轨迹上平均,
\(\begin{align} p(x^{(0)}) &= \int dx^{(1 ... T)} p(x^{(0 ... T)}) \frac{q(x^{(1 ... T)} \mid x^{(0)})}{q(x^{(1...T)} \mid x^{(0)})} \\ &= \int dx^{(1 ... T)} q(x^{(1...T)} \mid x^{(0)}) \frac{p(x^{(0...T)})}{q(x^{(1...T)} \mid x^{(0)})} \\ &= \int dx^{(1 ... T)} q(x^{(1...T)} \mid x^{(0)}) · p(x^{(T)}) \prod_{t=1}^T \frac{p(x^{(t-1)} \mid x^{(t)})}{q(x^{(t)} \mid x^{(t-1)})} \end{align}\) 这可以通过从正向轨迹 $q(x^{(1…T)} \mid x^{(0)})$ 平均样本来快速评估。对于对于无穷小 $\beta$,轨迹上的正向和反向分布可以相同(见2.2节)。如果它们是相同的,那么只需要 $q(x^{(1…T)} \mid x^{(0)})$ 中的单个样本来精确评估上述积分。这与统计物理学中的准静态过程的情况相对应。
Training
训练相当于最大化模型对数似然,
\[\begin{align} L &= \int dx^{(0)} q(x^{(0)}) \log p(x^{(0)}) \\ &= \int dx^{(0)} q(x^{(0)}) · \log[\int dx^{(1...T)} q(x^{(1 ... T)} \mid x^{(0)}) · p(x^{(T)}) \prod_{t=1}^T \frac{p(x^{(t-1)}\mid x^{(t)})}{q(x^{(t)} \mid x^{(t-1)})}] \end{align} \tag{10, 11}\]通过 Jensen 不等式有变分下限:
\(L \geq \int dx^{(0 ... T)} q(x^{(0 ... T)}) · \log [p(x^{(T)}) \prod_{t=1}^T \frac{p(x^{(t-1)} \mid x^{(t)})}{q(x^{(t)} \mid x^{(t-1)})})] \tag{12}\) 如附录B所述,对于扩散轨迹,这将减少到,
\[L \geq K \\ K = -\sum_{t=2}^T \int dx^{(0)} dx^{(t)} q(x^{(0)}, x^{(t)}) · D_{KL}(q(x^{(t-1)} \mid x^{(t)}, x^{(0)}) \| p(x^{(t-1)} \mid x^{(t)})) + H_q(X^{(T)} \mid X^{(0)}) - H_q(X^{(1)} \mid X^{(0)}) - H_p(X^{(T)}) \tag{14}\]其中可以分析计算熵和KL散度。这个界的推导与变分贝叶斯方法中对数似然届的推导类似。
在第2.3节中,如果正向和反向轨迹相同,对应于准静态过程,那么方程13中的不等式就变成了等式。
训练包括找到逆马尔可夫转移,最大限度地提高对数似然的下限。
\(\hat p(x^{(t-1)} \mid x^{(t)}) = \arg \max_{p(x^{(t-1)}) \mid x^{(t)})} K \tag{15}\) 表1给出了高斯和二项扩散的具体估计目标。
因此,估计概率分布的任务已简化为对设置高斯序列均值和协方差(或为伯努利试验序列设置状态翻转概率)的函数执行回归的任务。
Setting The Diffusion Rate $\beta_t$
在前向轨迹中 $\beta_t$ 的选择对于训练的模型的表现很重要。在AIS中,正确的中间分布时间表可以大大提高对数分区函数估计的准确性。在热力学中,在平衡分布之间移动时采取的时间表决定了损失多少自由能量。
在高斯扩散的例子中, 通过在 K 上梯度下降学习扩散时间表 $\beta_{2…T}$。 第一步的方差 $\beta_1$ 固定为一个小常数以避免过拟合。使用重参数技巧进行采样。
对于二项扩散,离散状态空间使具有 frozen noise 的梯度上升变得不可能。作者进而选择前向扩散时间表 $\beta_{1…T}$ 消除每个扩散步骤原始信号的常数步长 $\frac{1}{T}$, 产生一个 $\beta_t = (T - t + 1)^{-1}$ 的扩散率。
Multiplying Distributions, and Computing Posteriors
计算后验以进行信号去噪或推断缺失值等任务需要用第二个分布或有界正函数 $r(x^{(0)})$乘以模型分布 $p(x^{(0)})$, 产生新的分布 $\tilde p(x^{(0)}) \propto p(x^{(0)}) r(x^{(0)})$。
对于许多技术来说,乘以分布既昂贵又困难,包括变分自编码器、GSN、NADE和大多数图形学模型。然而,在扩散融合模型下,这是直接的,因为第二个分布可以被视为扩散过程中每个步骤的小扰动,也可以通常精确地乘以每个扩散步骤。图3和图5演示了使用扩散模型对自然图像进行去噪和 inpainting。以下各节描述了如何在扩散概率模型的背景下乘以分布。


Modified Marginal Distributions
首先,为了计算 $\tilde p(x^{(0)})$ , 作者通过对应的函数 $r(x^{(t)})$ 乘以每个中间分布。我们使用分布或马尔可夫转移上方的波浪号来表示它属于以这种方式修改的轨迹。 $\tilde p(x^{0…T})$是修改后的逆过程, 其从分布 $\tilde p(x^{(T)}) = \frac{1}{Z_T}p(x^{(T)})r(x^{(T)})$ 开始, 并且通过一系列中间分布处理:
\(\tilde p(x^{(t)}) = \frac{1}{\tilde Z_t} p(x^{(t)}) r(x^{(t)}) \tag{16}\) 其中 $\tilde Z_t$ 是对于第 $t$ 个中间分布的规范化常数。
Modified Diffusion Steps
Applying $r(x^{(t)})$
Choosing $r(x^{(t)})$
Entropy of Reverse Process
Conclusion
作者引入了一种建模概率分布的新算法,可以对概率进行精确采样和评估,并证明其在各种玩具和真实数据集上的有效性,包括具有挑战性的自然图像数据集。
对于这些测试中的每一项,都使用了类似的基本算法,表明该方法可以准确地建模各种分布。
大多数现有的密度估计技术必须牺牲建模能力,以保持可驾驭性和效率,采样或评估通常非常昂贵。
算法的核心包括估计马尔可夫扩散链的反向传播,该链将数据映射到噪声分布;随着步数的增加,每个扩散步骤的反分布变得简单易行。
该算法可以学习拟合任何数据分布,但仍然可以进行训练、精确地从采样和评估,并且可以直接操作条件分布和后验分布。