Abstract

通过将图像形成过程分解为去噪自编码器的顺序应用，扩散模型（DM）在图像数据和其他方面实现了最先进的合成结果。

此外，它们的公式允许用于无需再训练即可控制图像生成过程的引导机制。

然而，由于这些模型通常直接在像素空间中运行，因此强大的DM的优化通常会消耗数百个GPU天，并且由于顺序评估，推理成本很高。

为了在有限的计算资源上进行DM训练，同时保持其质量和灵活性，我们将它们应用于强大的预训练自编码器的隐空间。

与之前的工作不同，关于这种表示的训练扩散模型首次在降低复杂性和细节保存之间达到近乎最佳的点，大大提高了视觉保真度。

通过在模型结构中引入交叉注意力层，我们将扩散模型转化为强大而灵活的生成器，用于文本或边界框等一般常见输入，并以卷积方式进行高分辨率合成。

隐扩散模型（LDM）在图像绘画和类有条件图像合成方面获得了新的最先进分数，并在各种任务上具有高度竞争力的性能，包括文本到图像合成、无条件图像生成和超分辨率，同时与基于像素的DM相比，显著降低了计算要求。

Methods

为了降低训练扩散模型以进行高分辨率图像合成的计算需求，作者观察到，尽管扩散模型允许通过对相应的损失项进行降采样来忽略感知上无关紧要的细节，但它们仍然需要在像素空间中进行昂贵的函数评估，这导致对计算时间和能源产生巨大需求。

作者提出过将压缩与生成学习阶段明确分离来规避这一缺点（见图2）。为了实现这一目标，作者使用自编码器模型，该模型学习了一个感知等同于图像空间的空间，但计算复杂性显著降低。

这种方法有几个优势：

（i）通过跳跃高维图像空间，我们获得了计算效率更高的DM，因为采样是在低维空间上进行的。

（ii）作者利用了UNet架构[71]继承下来的DM的归纳偏置，这使得它们对具有空间结构的数据特别有效，因此减轻了之前方法[23、66]要求的侵略性、降低质量压缩水平的需求。

（iii）最后，获得了通用压缩模型，其隐空间可用于训练多个生成模型，也可以用于其他下游应用，如单图像CLIP引导合成[25]。

Perceptual Image Compression

作者的感知压缩模型基于之前的工作[23]，由感知损失[106]和基于 patch 的[33]对抗目标[20、23、103]训练的自编码器组成。这确保了通过强制执行局部真实将重建局限于图像流形，并避免了仅依靠L2或L1目标等像素空间损失而引入的模糊性。

更具体来讲， 给定一张图像 $x \in R^{H \times W \times 3}$， 编码器 $\varepsilon$ 编码 $x$ 到一个隐表征 $z \in \varepsilon(x)$, 解码器 $D$ 从隐空间重构图像， 有 $\tilde x = D(z) = D(\varepsilon(x))$， 其中 $z \in R^{h \times w \times c}$。 跟重要的事， 编码器以系数 $f = H / h = W / w$ 降采样图像， 作者调研了不同的降采样系数 $f = 2^m$。

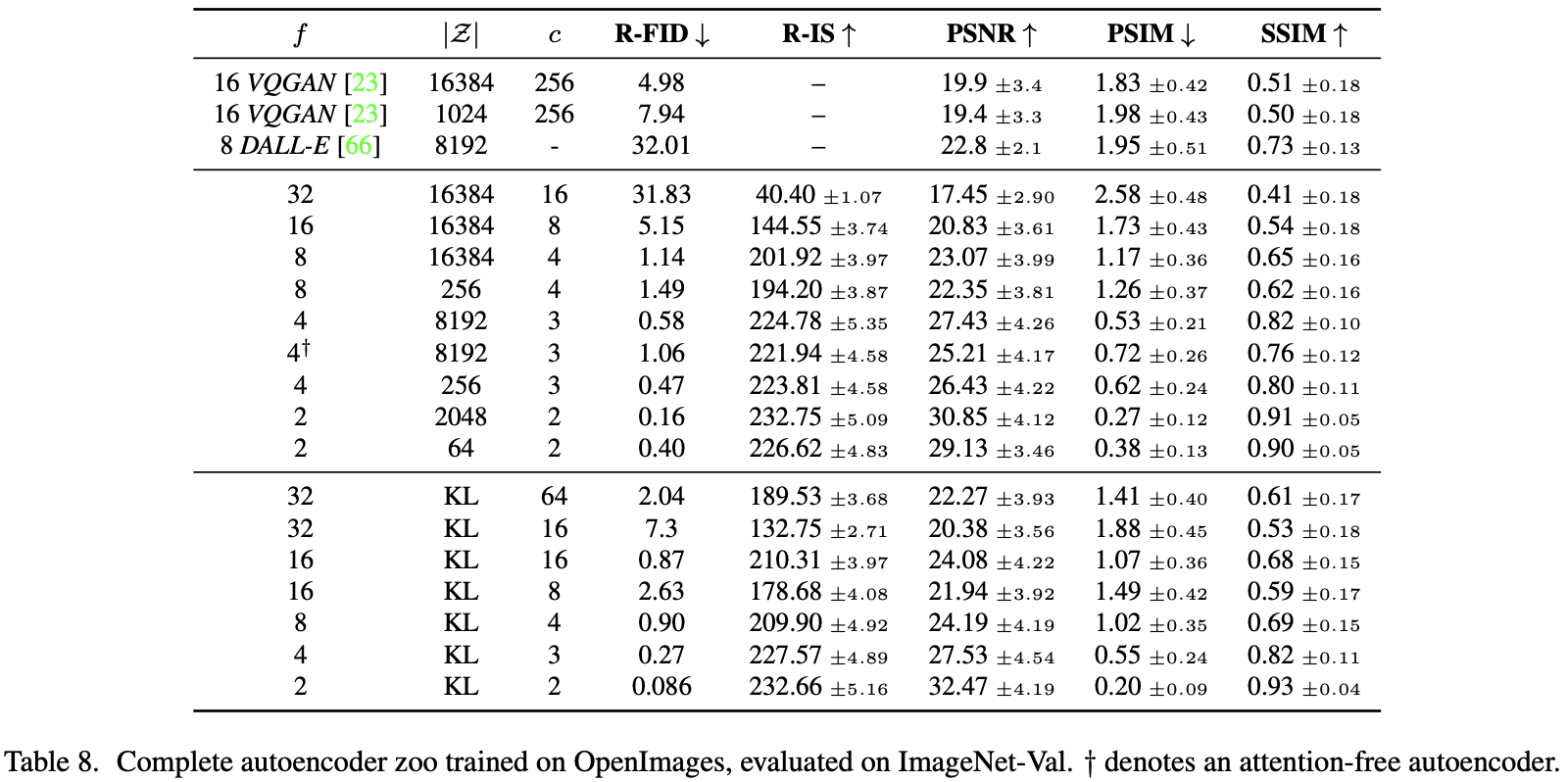
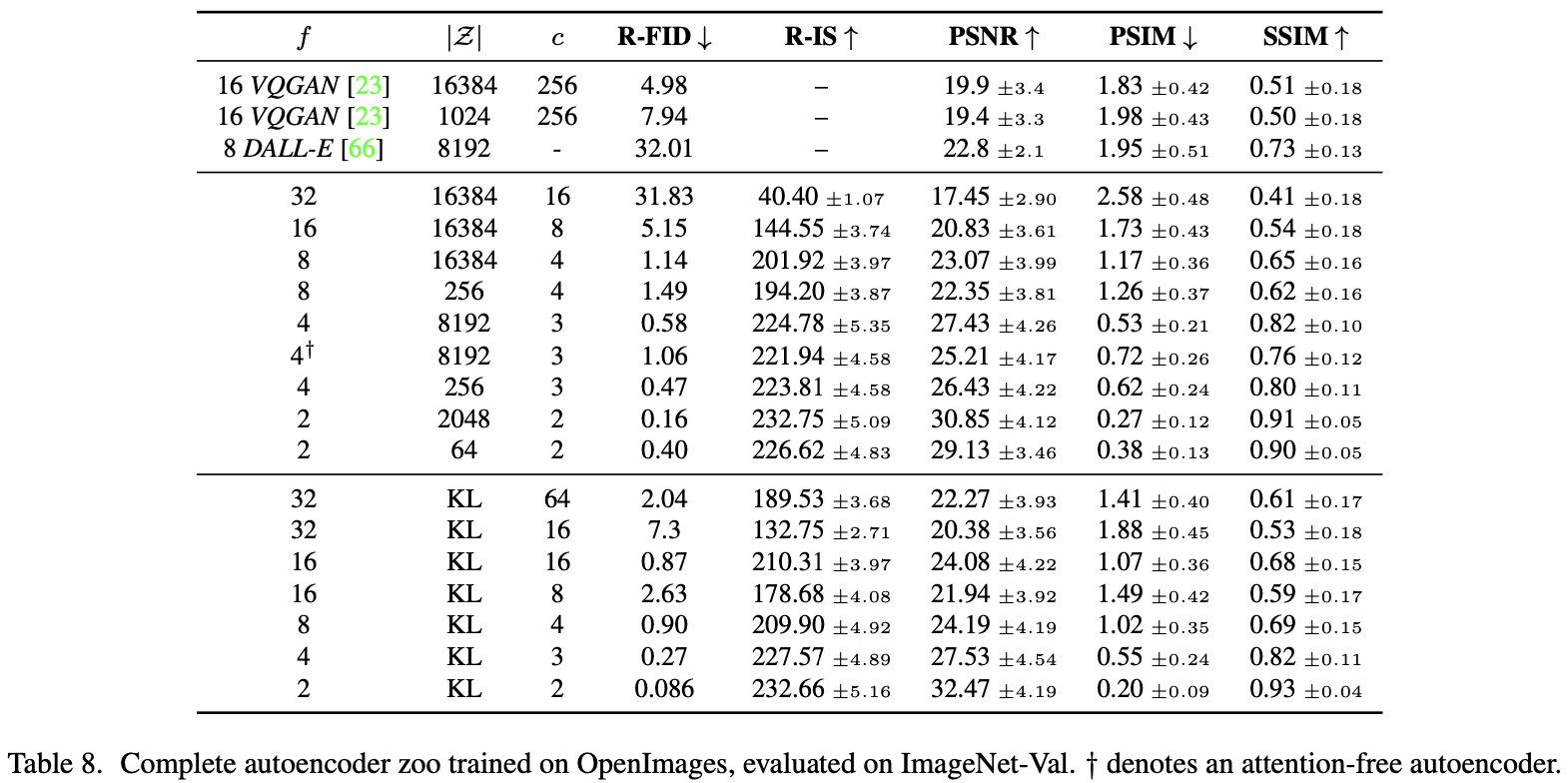
为了避免任意的高方差隐空间，作者实验了两种不同的正则化。第一个变体KL-reg， 对学习的隐空间对标准正态施加轻微的 KL 惩罚，类似于VAE[46, 69]，而 VQ-reg 在解码器中使用矢量量化层。该模型可以解释为VQGAN，但量化层集成在解码器。由于随后的DM旨在与学到的潜在空间 $z = \varepsilon(x)$ 的二维结构一起工作，因此可以使用相对温和的压缩率，并实现非常好的重建。这与之前的作品[23，66]形成鲜明对比，后者依靠学习空间 $z$ 的任意一维排序来模拟其分布自回归，从而忽略了 $z$ 的大部分固有结构。因此，我们的压缩模型更好地保留了 $x$ 的详细信息（见表 8 ）。

Latent Diffusion Models

Diffusion Models 是概率模型，旨在通过逐渐去噪正态分布变量来学习数据分布 $p(x)$，这相当于学习长度为 $T$ 的固定马尔可夫链的反向过程。对于图像合成，最成功的模型[15,30,72]依赖于 $p(x)$ 上变分下界的加权变体，该变体反映了去噪分数匹配[85]。这些模型可以解释为一个同等加权的去噪自编码器序列 $\epsilon(x_t, t); t=1, …, T$，这些自编码器被训练来预测其输入 $x_t$ 的去噪变体，其中 $x_t$ 是输入 $x$ 的噪声版本。对应的目标可以简化为：

\(L_DM = E_{x, \epsilon \thicksim N(0, 1), t} [\|\epsilon - \epsilon_\theta(x_t, t)\|_2^2]\) 其中 $t$ 从 {1… T} 中均匀采样。

Generative Modeling of Latent Representations 有了由 $\varepsilon$ 和 $D$ 组成的训练好的感知压缩模型， 我们现在可以进入一个高效、低维的隐空间，其中高频、难以察觉的细节被抽象出来。与高维像素空间相比，该空间更适合基于似然的生成模型，因为它们现在可以（i）专注于数据的重要、语义位，以及（ii）在较低的维度、计算效率更高的空间中训练。

与之前在高度压缩、离散的隐空间[23、66、103]中依赖自回归、基于注意力的 Transformer 模型的工作不同，我们可以利用我们的模型提供的特定图像归纳偏置。这包括主要从二维卷积层构建底层UNet的能力，并使用重新加权的边界进一步将目标集中在感知上最相关的位上，该边界现在为：

模型的神经主干 $\varepsilon_\theta(o, t)$ 实现为一个以时间为条件的 UNet。 由于前向过程是固定的， $z_t$ 可以在训练过程中从 $\varepsilon$ 高效地得到， 并且从 $p(z)$ 中采样可以通过 $D$ 解码到图像空间。

Conditioning Mechanisms

与其他类型的生成模型类似，扩散模型原则上能够建模 $p（z \mid y）$ 形式的条件分布。这可以通过条件去噪自编码器 $\epsilon_\theta(z_t，t，y)$ 实现，并通过文本[68]、语义图[33、61]或其他图像到图像的翻译任务[34]等输入 $y$ 来控制合成过程。

然而，在图像合成的背景下，将DM的生成力与类标签[15]或输入图像的模糊变体[72]以外的其他类型的条件相结合，是迄今为止未被探索的研究领域。

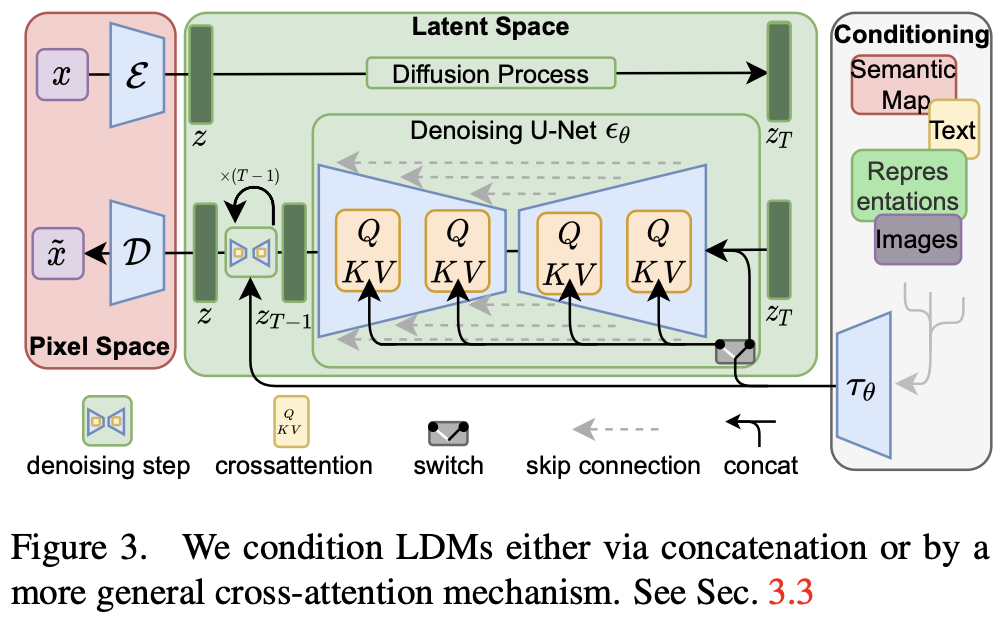
作者通过交叉注意力机制[97]增强DM的底层UNet主干结构，将DM转化为更灵活的条件图像生成器，这对于学习各种输入模态联系的基于注意力的模型[35,36]有效。为了从各种模态（如语言提示符）预处理 $y$ ，作者引入了一个特定于域的编码器 $\tau(\theta)$，该编码器将 $y$ 投影到中间表示 $\tau_\theta(y) \in R^{M \times d_\tau}$， 其通过一个交叉注意力层 $Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d}}) · V$ 被映射到 UNet的中间层。如图3所示。

基于图像-条件对， 学习条件 LDM 通过：

\(L_{LDM} := E_{\varepsilon(x), y, \epsilon \thicksim N(0, 1), t} [\| \epsilon - \epsilon_\theta(z_t, t, \tau_\theta(y)) \|_2^2]\) 其中 $\tau_\theta$ 和 $\epsilon_\theta$ 通过上式联合优化。这个条件机制是灵活地， 因为 $\tau_\theta$ 可以参数化为特定领域的专家， 例如当 $y$ 是文本提示时， 其是 Transformer。

Experiments

On Perceptual Compression Tradeoffs

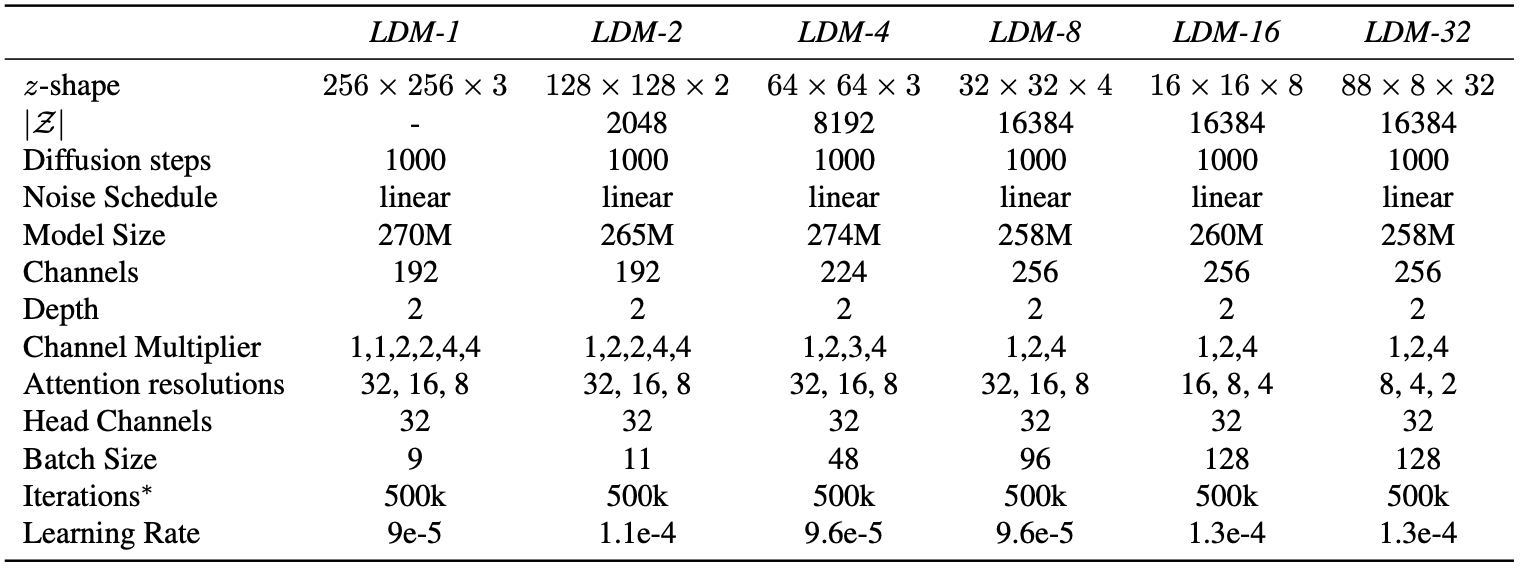
本节用不同的下采样因子 $f \in {1, 2, 4, 8, 16, 32}$ 分析 LDM 的表现（缩写为 LDM-f, 其中 LDM-1 对应于 pixel-based DMs ）。我们将所有实验的计算资源固定单个NVIDIA A100，并以相同数量的步骤和相同数量的参数训练所有模型。

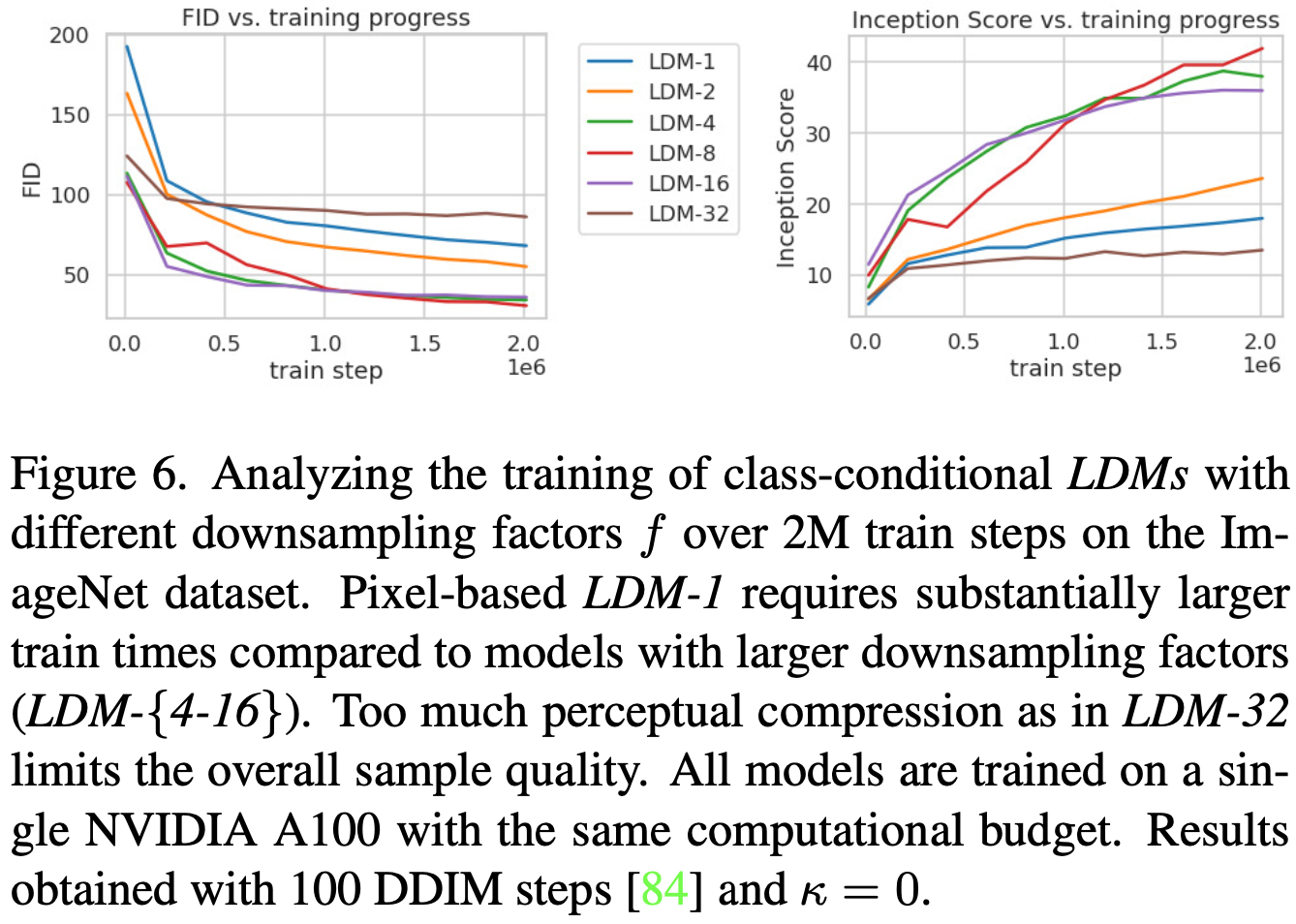
表8显示了本节比较的用于LDM的第一阶段模型的超参数和重建性能。图6显示了在 ImageNet 数据集上 class-模型的 2M步骤训练进度的样本质量。我们看到，i）LDM-{1,2}的下采样系数很小，导致训练缓慢，而ii）f 值过大，会导致保真度难以提升。重温上述分析（图1和图2），我们将此归因于 i）将大部分感知压缩留给扩散模型，ii）过于强的第一阶段压缩导致信息丢失，从而限制可实现的质量。LDM-{4-16}在效率和感知忠实的结果之间取得了良好的平衡，这表现在2M训练步骤后，基于像素的扩散（LDM-1）和LDM-8之间的 FID 差距为38。

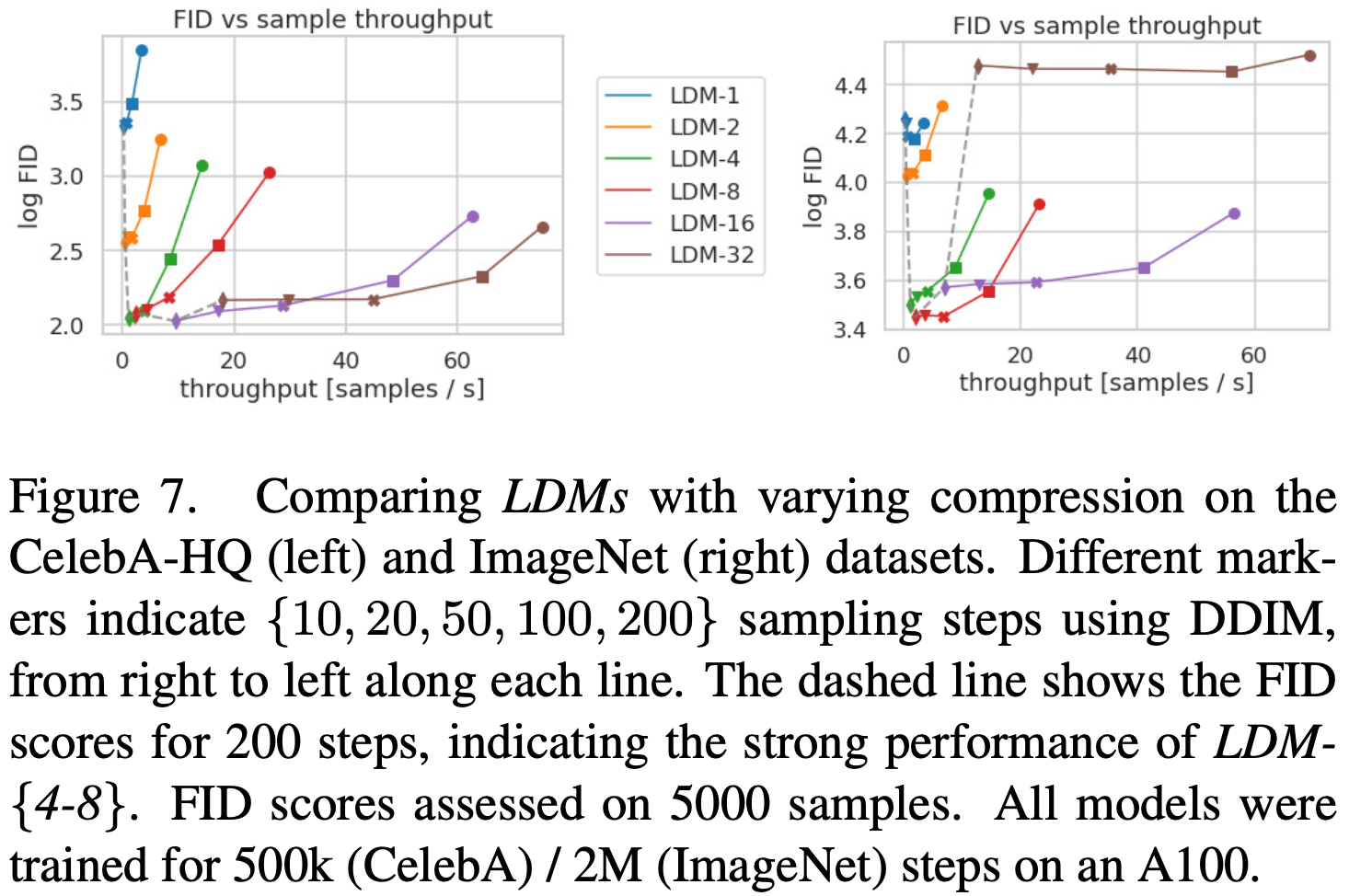
在图7中，我们将在 CelebA HQ 和 ImageNet 上训练的模型与 DDIM 采样器比较了不同数量的去噪步骤的采样速度，并根据FID分数进行绘制。LDM-{4-8}的表现优于感知和压缩比不恰当的模型。特别是与基于像素的LDM-1相比，它们的FID分数要低得多，同时显著提高了样本吞吐量。ImageNet等复杂数据集需要降低压缩，以避免降低质量。总之，LDM-4和-8为实现高质量合成结果提供了最佳条件。

Conditional Latent Diffusion

Transformer Encoders for LDMs

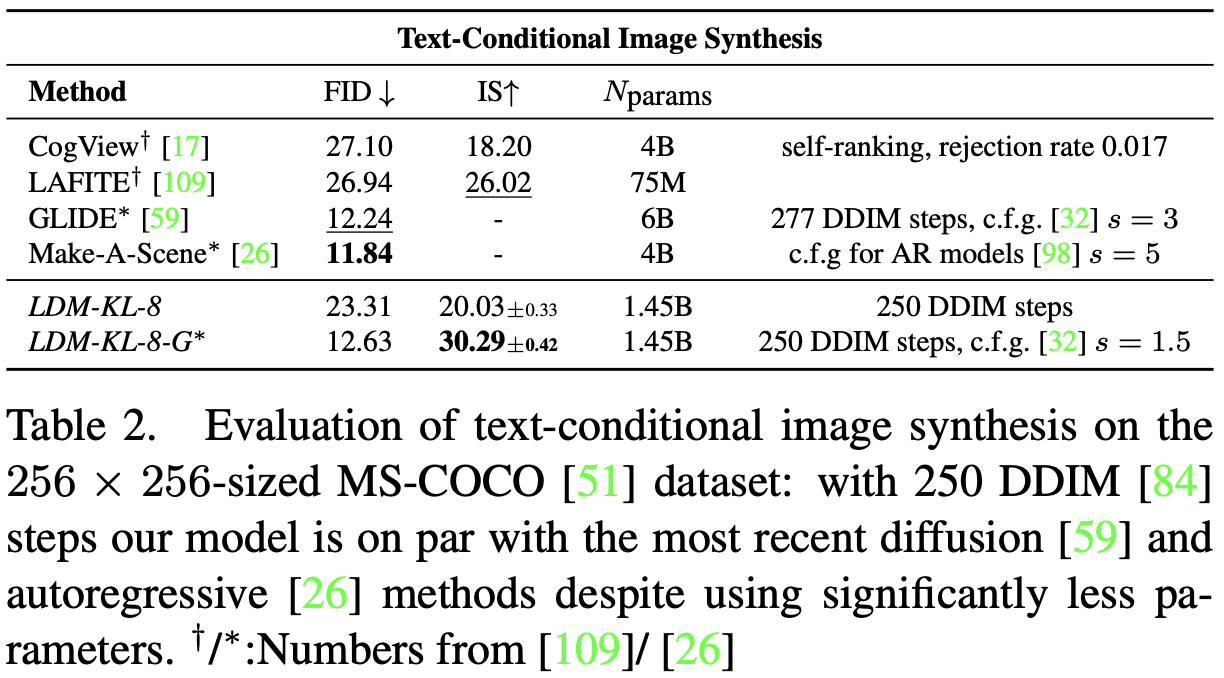
通过在LDM中引入基于交叉注意力的条件，我们打开了以前在扩散模型中未探索的各种条件模态。对于文本到图像图像建模，作者训练了一个1.45B参数 KL正则化 LDM，该参数以LAION-400M [78]上的语言提示为条件。其使用BERT-tokenizer[14]，并实现 $\tau_\theta$ 作为 Transformer [97]来推断一个隐编码，该编码通过（多头）交叉注意力映射到UNet。 这种学习语言表示和视觉合成的特定领域专家的组合产生了一个强大的模型，该模型很好地泛化到复杂的用户定义文本提示，参见图8和图5。为了进行定量分析，作者遵循之前的工作，并评估MS-COCO[51]验证集上的文本到图像生成，其中我们的模型改进了强大的AR[17，66]和基于GAN的[109]方法，参见表2。我们注意到，应用无分类器扩散引导[32]极大地提高了样本质量，因此引导的LDM-KL-8-G与最近用于文本到图像合成的最新AR[26]和扩散模型[59]相当，同时大幅减少了参数计数。为了进一步分析基于交叉注意力的调节机制的灵活性，我们还训练模型，根据OpenImages[49]上的语义布局合成图像，并在COCO[4]上进行微调，见图8。

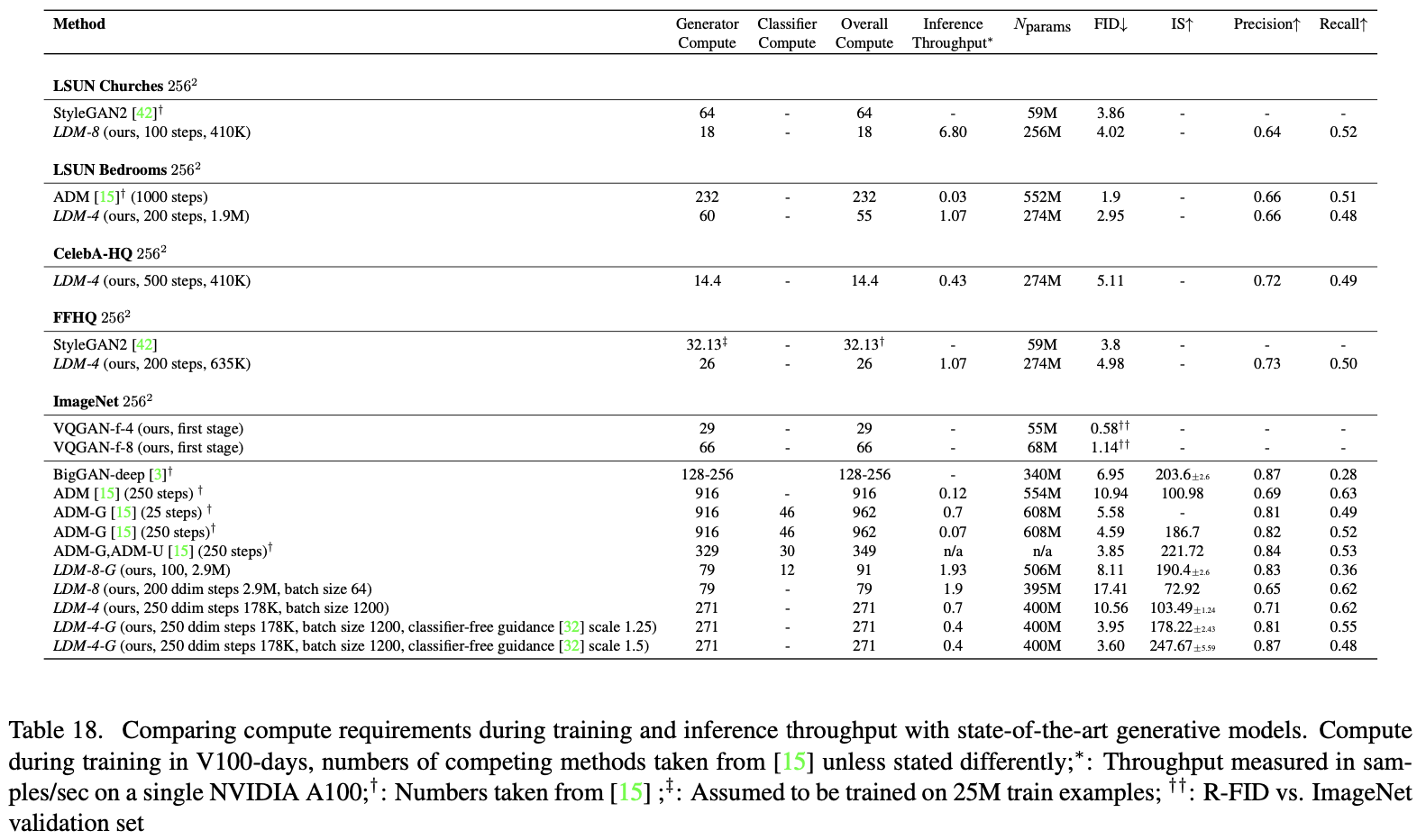
最后， 遵循之前的工作[3、15、21、23]，作者评估了最佳类条件ImageNet模型。在这里，我们的表现优于最先进的扩散模型ADM[15]，同时显著减少了计算要求和参数计数，参见表18。

Convolutional Sampling Beyond 256 x 256

通过将空间对齐的条件信息与 $\epsilon_\theta$ 的输入连接起来，LDM可以作为高效的通用图像到图像翻译模型。我们用它来训练语义合成、超分辨率的模型和绘画。对于语义生成，作者使用景观图像与语义映射配对，并将语义映射的下采样版本与 $f = 4$ 模型的隐图像表示连接起来（VQ-reg，见表8）。我们以 $256^2$ 的输入分辨率（从 $384^2$ 裁剪）进行训练，但发现我们的模型将尺寸推广到更大的分辨率，当以卷积方式评估时，可以生成高达百万像素的图像（见图9）。我们利用这种行为应用了超分辨率模型和绘画模型在 $512^2$ 和 $10242^$ 之间生成大图像。对于这种应用，信噪比（由隐空间的尺度计算）会显著影响结果。我们在学习LDM时说明了这一点：（i）$f = 4$ 模型提供的隐空间（KL-reg，见表8）和（ii）按组件标准差缩放的重新缩放版本。

后者与无分类器引导相结合，也可以直接合成文本条件 LDM-KL-8-G 的 $> 256^2$ 图像，如图13。

Super-Resolution with Latent Diffusion

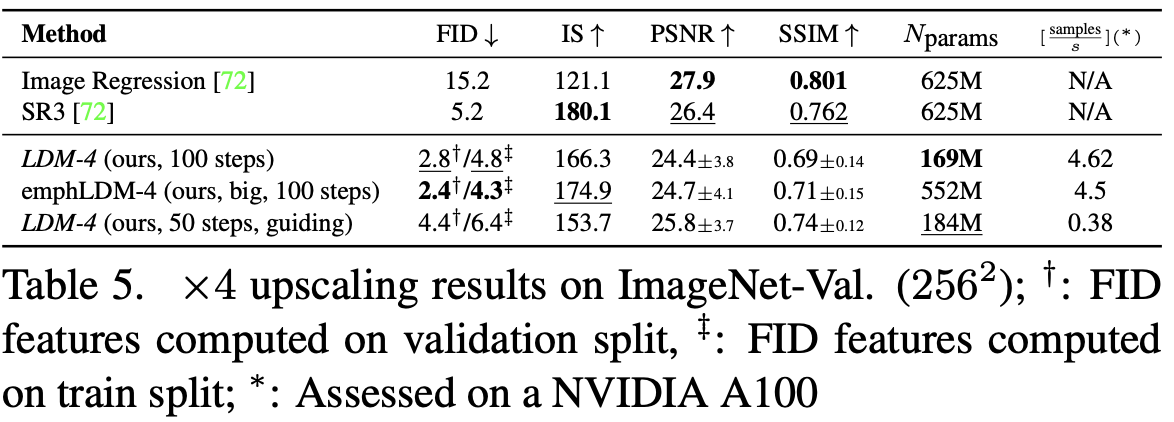
通过拼接对低分辨率图像进行直接的条件，可以有效地训练LDM以获得超分辨率。 在第一个实验中，我们遵循SR3，并根据SR3的数据处理流程在ImageNet上使用4×下采样将图像退化修复为双立方插值。我们使用OpenImages上预训练的 $f = 4$ 自编码模型（VQ-reg，参见表8）并将低分辨率条件 $y$ 和输入与 UNet 连接起来，即 $\tau_\theta$是恒等式。我们的定性和定量结果（见图10和表5）显示了有竞争力的性能，LDM-SR在FID中的表现优于SR3，而SR3的IS更好。一个简单的图像回归模型可以获得最高的PSNR和SSIM分数；然而，这些指标与人类感知不一致，比不完全对齐的高频细节更倾向于模糊。此外，我们进行了一项用户研究，将像素基线与LDM-SR进行比较。我们遵循SR3，在两张高分辨率图像之间向人类受试者展示低分辨率图像，并要求偏好。表4中的结果肯定了LDM-SR的良好性能。PSNR和SSIM可以通过使用 post-hoc 引导机制[15]来推动，我们通过感知损失实现此基于图像的引导器。

由于双立方退化过程不能很好地泛化到不遵循此预处理的图像，作者还通过使用更多的逆退化来训练一个通用模型LDM-BSR。

Inpainting with Latent Diffusion

绘画的任务是用新内容填充图像的 mask 区域，要么是因为图像的一部分被损坏，要么是替换图像中现有但不需要的内容。我们评估了我们的条件图像生成的一般方法与这项任务的更专业化、最先进的方法相比如何。我们的评估遵循LaMa[88]的协议，这是一个最近的绘画模型，引入了依赖于Fast Fourier Convolutions的专用架构[8]。

我们首先分析了第一阶段不同设计选择的影响。特别是在KL和VQ正则化方面，我们将LDM-1（即基于像素的条件DM）与LDM-4进行了比较，并在第一阶段无注意力比较了VQ-LDM-4（见表8），后者减少了用于高分辨率解码的GPU内存。为了具有可比性，我们固定了所有模型的参数数量。表6报告了 $256^2$ 和 $512^2$ 训练和采样吞吐量，每个epoch的总训练时间（以小时为单位），以及 6 epoch 后验证的FID分数。总体而言，我们观察到基于像素和隐扩散模型之间的速度至少为2.7倍，同时将FID分数提高至少1.6倍。

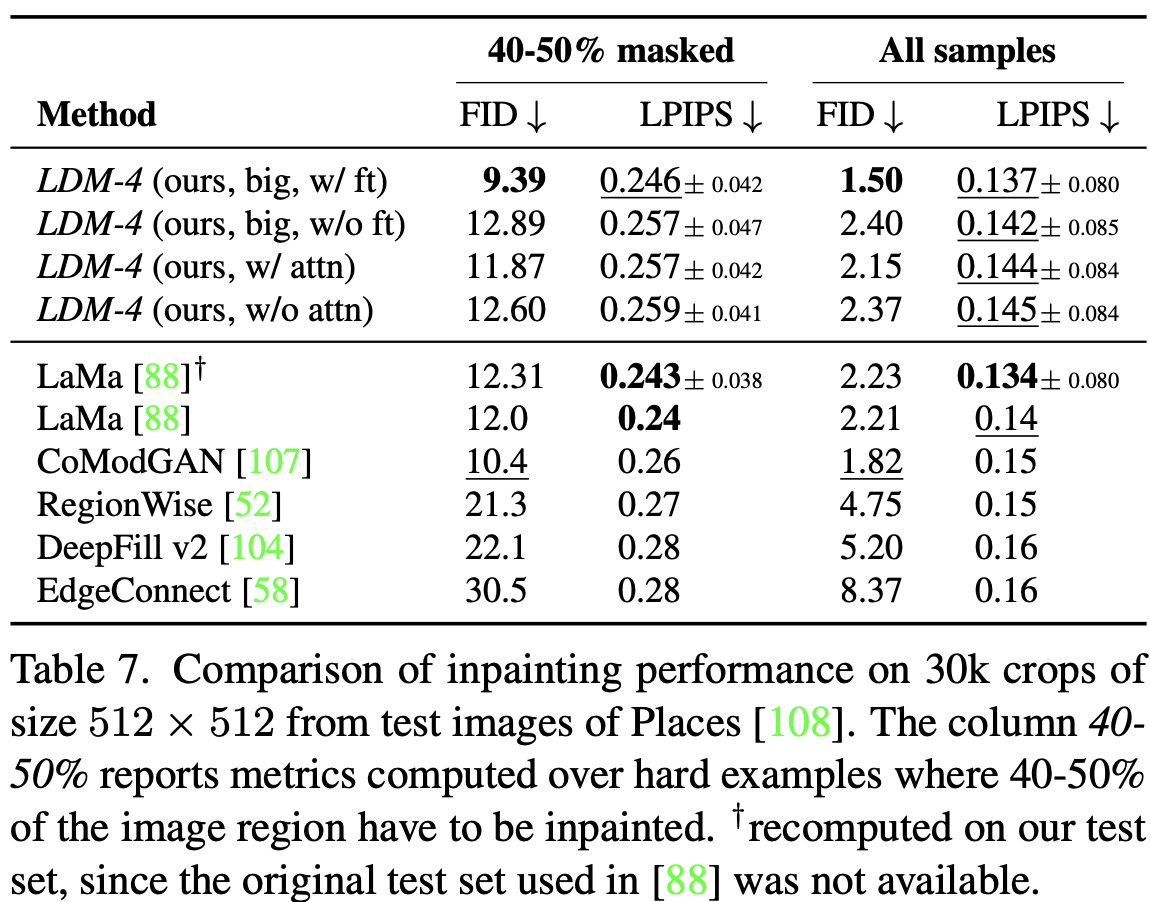
与表7中其他绘画方法的比较表明，我们的模型比[88]相比，我们的模型提高了FID测量的整体图像质量。未 mask 图像和我们的样本之间的LPIPS略高于[88]。我们将此归因于[88]只产生一个结果，与我们的 LDM 提供的多样化结果相比，该结果往往会恢复更多的平均图像。此外，在一项用户研究（表4）中，人类更喜欢我们的结果，而不是[88]的结果。

基于这些初步结果，在没有注意力的情况下，在VQ正则化第一阶段的隐空间中训练了一个更大的扩散融合模型（在表7中很大）。随后[15]，该扩散模型的UNet在其特征层次结构的三个级别上使用注意力层，即用于上下采样的BigGAN残差块，并具有387M参数，而不是215M。经过培训，我们注意到 $256^2$ 和 $512^2$ 分辨率生产的样本质量存在差异，我们假设这是额外的注意力模块造成的。然而，在 $512^2$ 分辨率下对模型进行半个 epoch 的微调，可以使模型适应新特征统计信息，并在图像绘画上设置新的最先进的FID。

Appendix

D. Additional Results

D.6. Super-Resolution

为了更好地在像素空间中将 LDM和扩散模型之间进行比较，我们从表5中扩展了我们的分析，将训练为相同步骤和参数数量为相当的扩散模型与LDM比较。这种比较的结果显示在表11的最后两行中，并表明LDM实现了更好的性能，同时允许更快的采样。图20进行了定性比较，显示了像素空间中LDM和扩散模型的随机样本。

D.6.1 LDM-BSR: General Purpose SR Model via Diverse Image Degradation

为了评估 LDM-SR 的泛化能力，我们将其应用于 Conditional ImageNet 模型的合成 LDM 样本和从互联网上爬出来的图像。有趣的是，我们观察到，仅使用 bicubicly 下采样条件训练的 LDM-SR 不能很好地泛化到不遵循这种预处理的图像。因此，为了获得各种现实世界图像的超分辨率模型，该模型可以包含相机噪声、压缩伪影、模糊和插值的复杂叠加，我们用[105]的退化流程取代了 LDM-SR 中的 bicubic 下采样操作。BSR退化过程以随机顺序将JPEG压缩噪声、相机传感器噪声、不同的图像插值进行下采样、高斯模糊核和高斯噪声应用于图像。我们发现，使用[105]中原始参数的 BSR 退化过程会导致非常强的退化。由于更温和的退化过程似乎适合我们的应用，我们调整了 BSR 退化的参数。图18通过直接比较 LDM-SR 和 LDM-BSR 来说明这种方法的有效性。后者产生的图像比仅限于固定预处理的模型清晰得多，使其适合现实世界的应用。

E. Implementation Details and Hyperparameters

E.2. Implementation Details

E.2.1 Implementations of $\tau_\theta$ for conditional LDMs

对于 text-to-image 和 layout-to-image 生成的实验， 我们实现条件器 $\tau_\theta$ 作为一个 unmask 的 Transformer， 其处理一个 tokenized 的输入 $y$， 产生一个输出 $\xi := \tau_\theta(y)$， 其中 $\xi \in R^{M \times d_\tau}$。 更具体地说， Transformer 由 N 个 Transformer Block 实现，这些 Transformer Block 由全局自注意层、层归一化和 position-wise MLP组成，如下所示：

有了 $\xi$， 条件通过 图3所示 的 cross-attention 机制映射入 UNet。

G. Details on Autoencoder Models

我们以对抗训练的方式训练所有的自编码器模型， 因此，对优化基于 Patch 的判别器 $D_\psi$，以区分原始图像和重建 $D(E(x))$。为了避免任意缩放隐空间，我们将隐变量 $z$ 正则化为零中心，并通过引入正则化损失项 $L_{reg}$ 获得小方差。 我们研究了两种不同的正则化方法：(i) 一个在 $q_E(z \mid x) = N(z; E_\mu, E_{\sigma^2})$ 和 标准正态分布 $N(z; (0, 1))$ 之间的 low-weighted Kullback-Leibler 项， 作为一个标准自编码器； (ii) 通过学习 $\mid Z \mid$ 不同样本的码表使用 vector quantization 层正则化隐空间。为了获得高保真重建，我们对这两种情况都只使用非常小的正则化。 我们将 KL 项以系数 $~ 10^{-6}$ 加权或选择一个高维度的码表 $\mid Z \mid$。

训练自编码器模型 $(E, D)$ 的完整目标为：

DM Training in Latent Space 请注意，对于在学习的隐空间上训练扩散模型，我们在学习时再次区分两种情况 $p(z)$ 或者 $p(z \mid y)$： (i) 对于 KL 正则的隐空间， 我们采样 $z = E_\mu(x) + E_{\sigma}(x) · \epsilon =: E(x)$, 其中 $\epsilon \thicksim N(0, 1)$。 在重新缩放隐变量时，我们估计了分量方差：

来自于数据的第一批量， 其中 $\hat \mu =\frac{1}{bchw} \sum_{b, c, h, w} z^{b, c, h, w}$。 $E$ 的输出被缩放以便缩放后的隐变量有单位标准差, $z \leftarrow \frac{z}{\hat \sigma} = \frac{E(x)}{\hat \sigma}$ 。 (ii) 对于 VQ-regularized 隐空间， 我们在量化层前提取 $z$， 并且将量化操作加入解码器， 例如将其作为 $D$ 的第一层。

• Previous
  【深度学习】PointPillars: Fast Encoders for Object Detection from Point Clouds
• Next
  【深度学习】Plug-and-Play Image Restoration with Deep Denoiser Prior