Abstract

当前的人类检测器要么以滑动窗口方式扫描图像，要么对一组离散的提议进行分类。

作者提出了一个基于将图像解码为一组人检测的模型。

该系统以图像为输入，并直接输出一组不同的检测假设。

由于一起生成预测，因此不需要常见的后处理步骤，如非极大值抑制。

作者使用循环LSTM层进行序列生成，并使用新的损失函数端到端训练模型，该函数对一组检测进行操作。

作者展示了在人群场景中检测人这一具有挑战性任务中方法的有效性。

Model

Overview

深卷积架构，如[11，17]构建对各种任务有效的图像表征。这些架构被用于检测，尽管主要是通过将它们调整为分类或回归框架。深度表征有足够的能力共同编码多个实例的外观，但必须用多个实例预测的组件来增强它们，以实现这一潜力。在本文中，作者考虑了循环神经网络（RNN），特别是 LSTM 单元作为此类组件的候选。使深度CNN与基于RNN的解码器相结合具有吸引力的关键属性是（1）直接利用强大的深度卷积表示的能力，以及（2）生成可变长度相干预测集的能力。这些属性已在[10]中成功用于生成图像字幕，并在[16]中用于机器翻译。在这个中，生成相干集的能力尤为重要，因为系统需要记住以前生成的预测，并避免对同一目标进行多次预测。

作者构建了一个模型，首先通过卷积架构（例如[17]）将图像编码为高级描述子，然后将该表示解码为一组边界框。作为预测可变长度输出的核心，作者建立了一个循环的LSTM单元。模型的概述见图2。

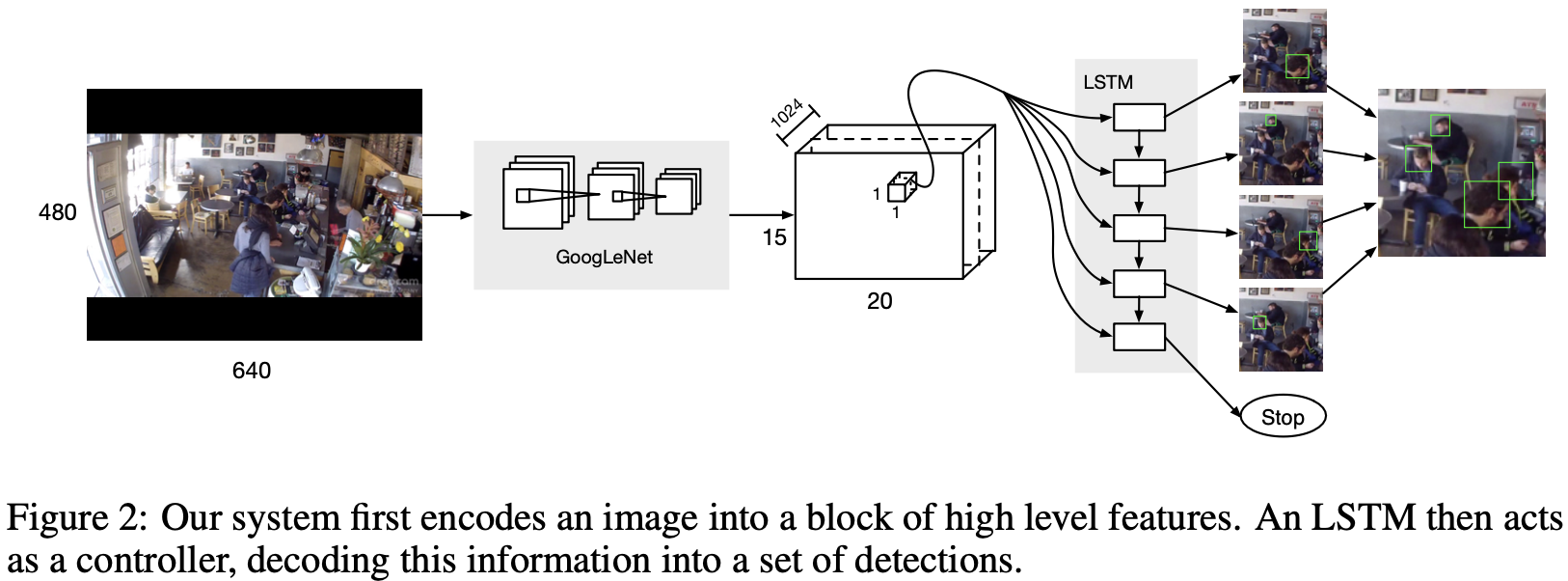
作者将每张图像转换为一个由1024维特征描述子的网格，遍布整个图像的跨区域。1024维度矢量总结了该区域的内容，并携带了有关物体位置的丰富信息。LSTM从此信息源中提取，并作为区域解码的控制器。在每个步骤中，LSTM都会输出一个新的边界框，并相应地相信在该位置会找到一个以前未被发现的人。鼓励按照置信度下降的顺序生产边界框。当LSTM无法在该地区找到置信度高于预定阈值的另一个边界框时，将生成一个停止符号。输出序列被收集起来，并作为该区域所有目标实例的最终描述。

Loss function

第 2.1 节中引入的架构预测一组候选边界框，以及对应于每个框的置信度分数。假设是按顺序生成的，后来的预测取决于之前的假设，通过LSTM的内存状态。在每次循环， LSTM 输出一个目标边界框 $b = {b_{pos}, b_c}$， 其中 $b_{pos} = (b_x, b_y, b_w, b_h) \in R^4$ 是相对位置， 边界框的宽和高， $b_c \in [0, 1]$ 是置信度。 在测试时，置信度低于阈值(如0.5)将被解释为停止符号。边界框置信度的较高值 $b_c$ 应该表明该框更有可能对应于真阳。作者将相应的真实边界框集表示为 $G = {b^i | i = 1, . . . , M }$，模型生成的候选边界框集表示为 $C = {\tilde b^j | j = 1, . . . , N }$。在下面，作者引入一种适合引导学习过程实现预期输出的损失函数。

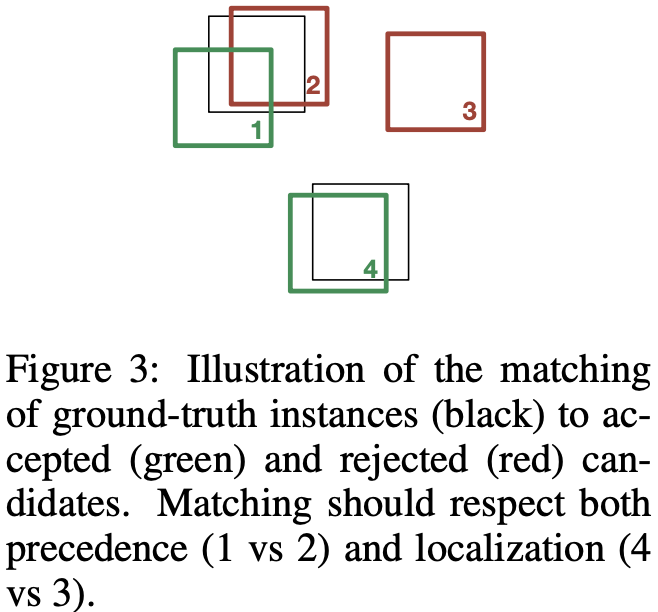
以图3中的示例为例，该示例示意图显示了一个具有四个生成假设的检测器，每个假设都按其预测步骤编号，将其表示为排名。注意典型的检测错误，如假阳（假设3）、不精确的定位（假设1）以及对相同真实边界框的多次预测（假设1和2）。不同的错误需要不同类型的反馈。在假设1的情况下，必须对边界框的位置进行微调。相反，假设3是假阳性的，模型应该通过分配低置信度分数来放弃预测。假设2是假设1报告的对目标的第二个预测，也应该放弃。为了捕捉这些关系，作者引入了一种匹配算法，为每个真实边界框分配一个唯一的候选假设。该算法返回一个 injective function $f: G \rightarrow C$， 例如 $f(i)$ 是分配给真实假设 $i$ 的候选假设的索引。

给定 $f$， 定义在集合对 $G$ 和 $C$ 上的损失函数为：

\(L(G, C, f) = \alpha \sum_{i=1}^{\mid G \mid} l_{pos}(b_{pos}^i, \tilde b_{pos}^{f(i)}) + \sum_{j=1}^{\mid C \mid} l_c (\tilde b_c^j, y_j)\) 其中 $l_{pos} = | b_{pos}^i - \tilde b_{pos}^{f(i)} |_1$ 真实位置和候选假设之间的误差, $l_c$ 是候选置信度的交叉熵损失， 其将会匹配到真实值。交叉熵损失的标签由 $y_j$ 提供。它由匹配函数 $y_j = 1{f^{-1}(j) \neq \emptyset}$ 定义。$\alpha$ 是置信度误差和定位误差的权衡。我们用交叉验证设置了$\alpha = 0.03$。请注意，对于固定匹配，可以通过反向传播此损失函数的梯度来更新网络。

作为一种朴素的极限， 作者考虑了一种基于真实边界框固定顺序的简单匹配策略。作者按图像位置从上到下以及从左到右对真实框进行排序。这种固定顺序匹配按顺序将候选框分配到排序的真实框。作者将此匹配函数称为“固定顺序”匹配，将其称为 $f_{fix}$，并将相应的损失函数称为 $L_{fix}$。

Hungarian loss: 固定顺序匹配的局限性在于，当解码过程产生假阳性或假阴性时，它可能会错误地将候选假设分配给真实实例。对于 $f_{fix}$ 选择的任何特定顺序，这个问题仍然存在。因此，作者探索了考虑 $C$ 和 $G$ 中元素之间所有可能的一对一赋值的损失函数。

回想一下，该模型的原则目标之一是在多个对象上输出一系列连贯的预测。作者定义了生成过程的停止标准，当预测分数低于指定阈值时。为了使这样的分数阈值有意义，必须鼓励模型在序列的早期生成正确的假设，并避免在高置信度预测之前生成低置信度预测。因此，当两个假设都与相同的真实边界框重叠时（例如图3中的假设1和2），我们更喜欢匹配预测序列中早些时候出现的假设。

为了使这个概念形式化，作者引入了假设和基本真理之间的以下比较函数：

\(\Delta (b_i, \tilde b_j) = (o_{ij}, r_i, d_{ij}) \tag{2}\) 函数 $\Delta: G \times C \rightarrow N \times N \times R$ 返回一个元组， 其中 $d_{ij}$ 是边界框位置之间的 $L_1$ 距离， $r_j$ 是排序或者 LSTM 预测序列输出的 $\tilde b_j$ 的索引， $o_{ij} $ 是一个惩罚与真实实例重叠不足的假设的变量。在这里，重叠的标准要求候选的中心位于真实边界框的范围内。 变量 $o_{ij}$ 使得展示了定位和检测误差的区别。由 $\Delta$ 定义了元组的词典顺序。 也就是说，在评估两个假设中的哪一个将被分配给一个真实边界框时，重叠是最重要的，然后是等级，然后是细粒度的定位。

根据方程2中比较函数 $\Delta$ 的定义，作者通过匈牙利算法找到了 $C$ 和 $G$ 在多项式时间内的最小成本二分匹配。请注意，匈牙利算法适用于任何具有明确定义的加法和配对比较操作的边权重图。为此，我们将（+）定义为元素加法，并将（<）定义为词典比较。例如，在图3中，正确匹配假设 1 和 4 将花费 $(0，5，0.4)$，而匹配1和3将花费 $(1，4，2.3)$，匹配 2 和 4 将花费$(0，6，0.2)$ 。请注意，用于检测重叠的第一项如何正确处理假设级别较低但离地面真相太远而无法进行合理匹配的情况（如图3中假设3的情况）。我们将此匹配的相应损失称为匈牙利损失，并表示为 $L_{hung}$。

Conclusion

• Previous
  【深度学习】Plug-and-Play Image Restoration with Deep Denoiser Prior
• Next
  【深度学习】Generative Modeling by Estimating Gradients of the Data Distribution