这篇博客文章关注的是生成建模的一个有前途的新方向。我们可以在大量的噪声扰动数据分布上学习分数函数(对数概率密度函数的梯度)，然后用朗之万型采样生成样本。这种生成模型方法通常被称为基于分数的生成模型，与现有模型家族相比具有几个重要的优势:无需对抗性训练的 GAN 级样本质量，灵活的模型架构，精确的对数似然计算，以及无需重新训练模型的逆问题解决。

Introduction

现有的生成建模技术可以根据它们表示概率分布的方式大致分为两类。

• 基于似然的模型， 通过(近似)最大似然直接学习分布的概率密度(或质量)函数。典型的基于似然的模型包括自回归模型、归一化流模型、基于能量的模型(EBMs)和变分自编码器(VAEs)。
• 隐式生成模型， 其中概率分布隐式地表示为采样过程的模型。最突出的例子是生成对抗网络(GANs)，其中通过使用神经网络转换随机高斯向量来合成来自数据分布的新样本。

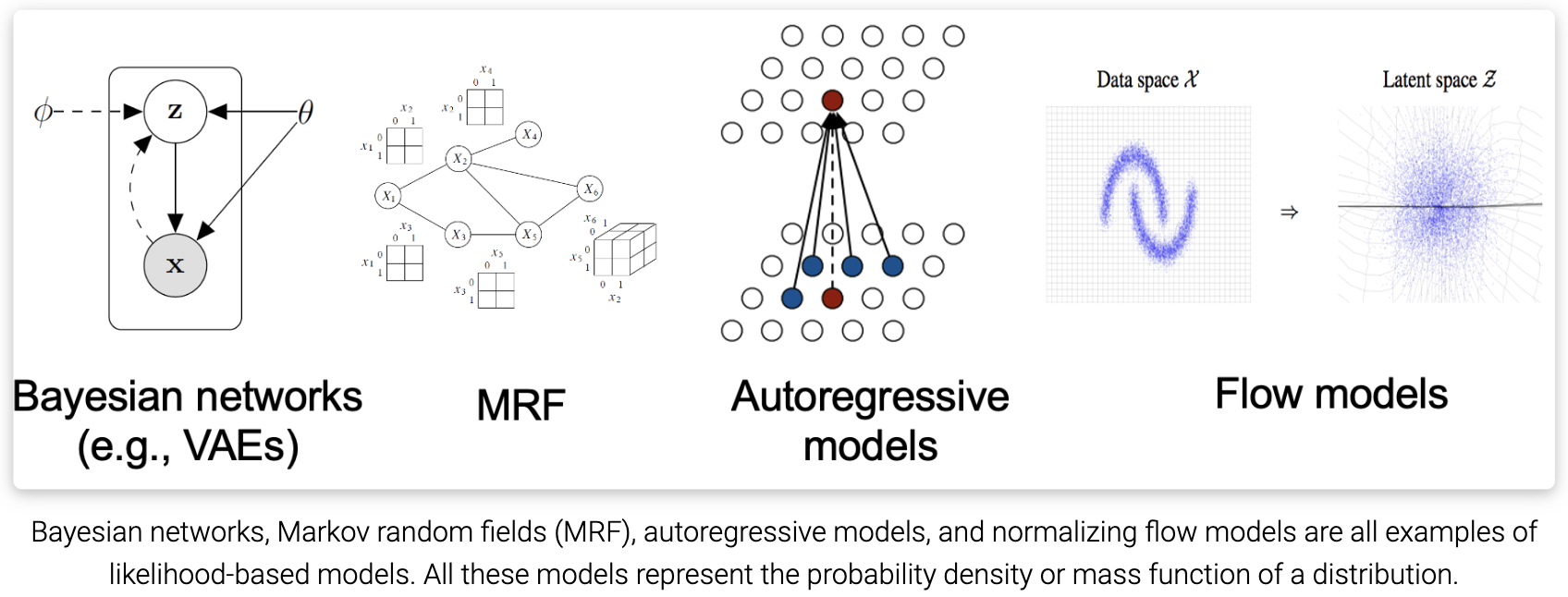
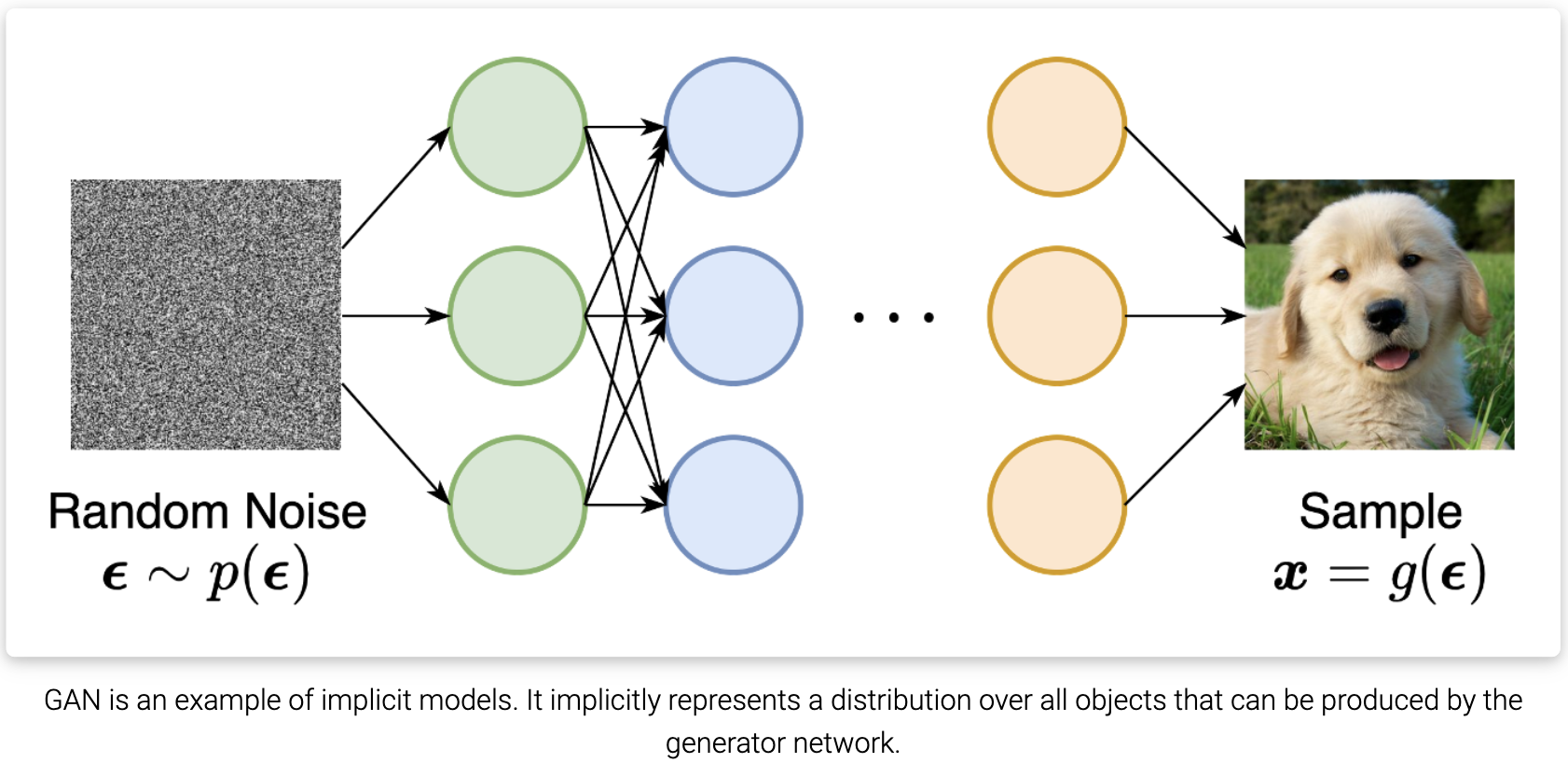然而，基于似然的模型和隐式生成模型都有很大的局限性。基于似然的模型要么需要对模型架构进行严格限制，以确保可处理的归一化常数用于似然计算，要么必须依赖代理目标来近似最大似然训练。另一方面，隐式生成模型通常需要对抗性训练，这是出了名的不稳定，并可能导致模式崩溃。

在这篇博文中，将介绍另一种表示概率分布的方法，这种方法可能会规避这些限制。关键思想是对对数概率密度函数的梯度进行建模，这个量通常被称为(Stein)分数函数。这种基于分数的模型不需要有可处理的归一化常数，可以通过分数匹配直接学习。

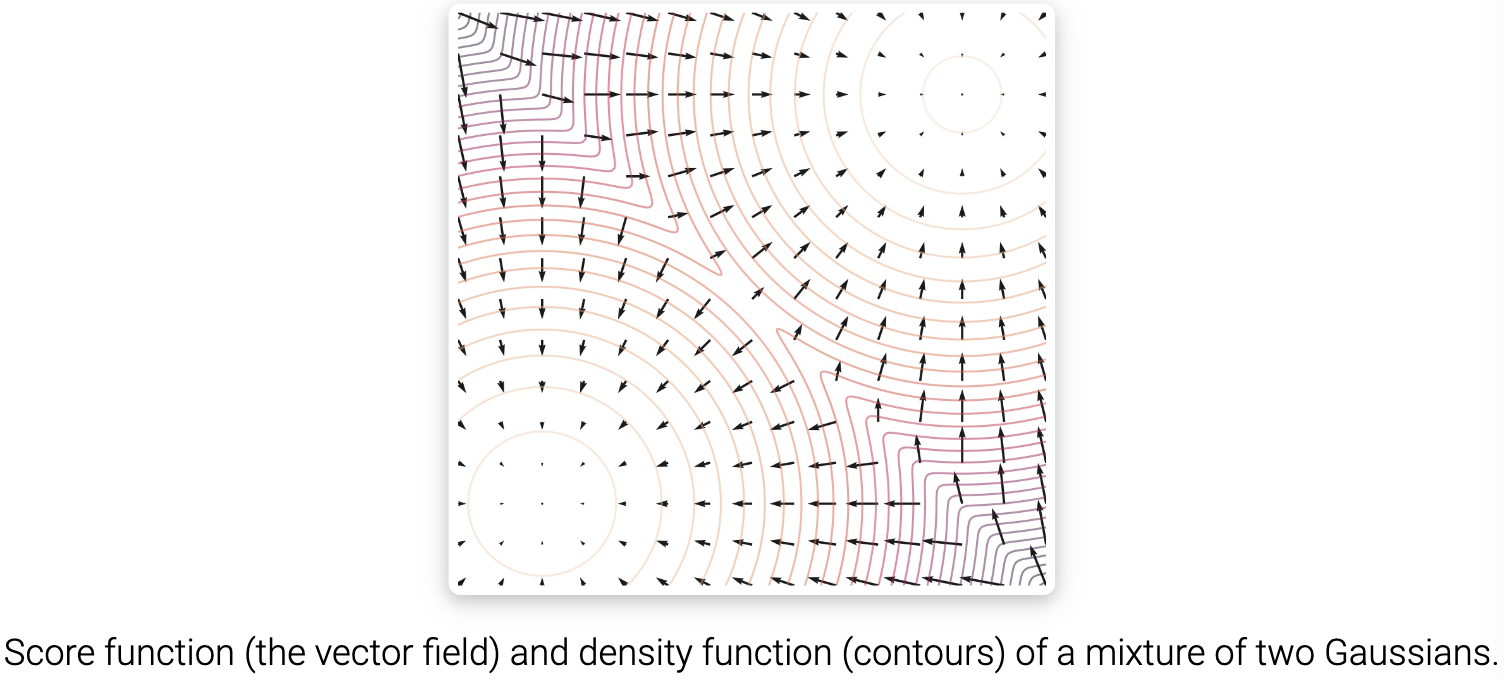
基于分数的模型已经在许多下游任务和应用程序上实现了最先进的性能。这些任务包括图像生成(是的，比GANs更好!)、音频合成、形状生成和音乐生成。此外，基于分数的模型与归一化流模型有联系，因此允许精确的似然计算和表示学习。此外，建模和估计分数有助于逆问题的解决，应用如图像修补、图像着色、压缩感知和医学图像重建(例如，CT, MRI)。

这篇文章旨在向你展示基于分数的生成建模的动机和直觉，以及它的基本概念、属性和应用。

The score function, score-based models, and score matching

假设我们有一个数据集 ${x_1, x_2，，x_N}$，其中每个点都独立于底层数据分布 $p(x)$ 。对于这个数据集，生成式建模的目标是将模型拟合到数据分布中，这样我们就可以通过从分布中采样来随意合成新的数据点。

为了建立这样一个生成模型，我们首先需要一种表示概率分布的方法。与基于似然的模型一样，其中一种方法是直接对概率密度函数(p.d.f.)或概率质量函数(p.m.f.)建模。设 $f_\theta(x) \in R$ 是一个由可学习参数 $\theta$ 参数化的实值函数。我们可以定义一个 p.d.f. 通过：

其中 $Z_\theta > 0$ 是依赖于 $\theta$ 的归一化常数，以便 $\int p_\theta(x) dx = 1$。 这里函数 $f_\theta(x)$ 通常被叫做未归一化的概率模型或者基于能量的模型。

我们可以训练 $p_\theta(x)$ 通过最大数据的对数似然：

\(\max_\theta \sum_{i=1}^N \log p_\theta(x_i)\) 然而， 上式需要 $p_\theta(x)$ 被归一化概率密度函数。 这是不希望的， 因为为了计算 $p_\theta(x)$， 对于任意 $f_\theta(x)$， 我们必须评估规范化常数 $Z_\theta - a$， 这通常是无迹可寻的。 因此，为了使最大似然训练可行，基于似然的模型必须限制其模型架构(例如，自回归模型中的因果卷积，归一化流模型中的可逆网络)以使 $Z_\theta$ 有迹可循，或者近似归一化常数(例如，VAEs中的变分推理，或对比散度中使用的MCMC采样)，这可能计算成本很高。

通过对分数函数而不是密度函数建模，我们可以避免难以处理的常数归一化的困难。分布 $p(x)$ 的分数函数定义为：

对这个分数函数建模的模型被叫做基于分数的模型， 表示为 $s_\theta(x)$。 基于分数的模型学习 $s_\theta(x) \approx \nabla_x \log p(x)$， 并且可以无需担心归一化常数被参数化。例如，我们可以很容易地用公式(1)中定义的基于能量的模型参数化基于分数的模型，通过：

注意到基于分数的模型 $s_\theta(x)$ 是独立于归一化常数 $Z_\theta$ 的。这极大地扩展了我们可以使用的模型家族，因为我们不需要任何特殊的结构来使规范化常数易于处理。

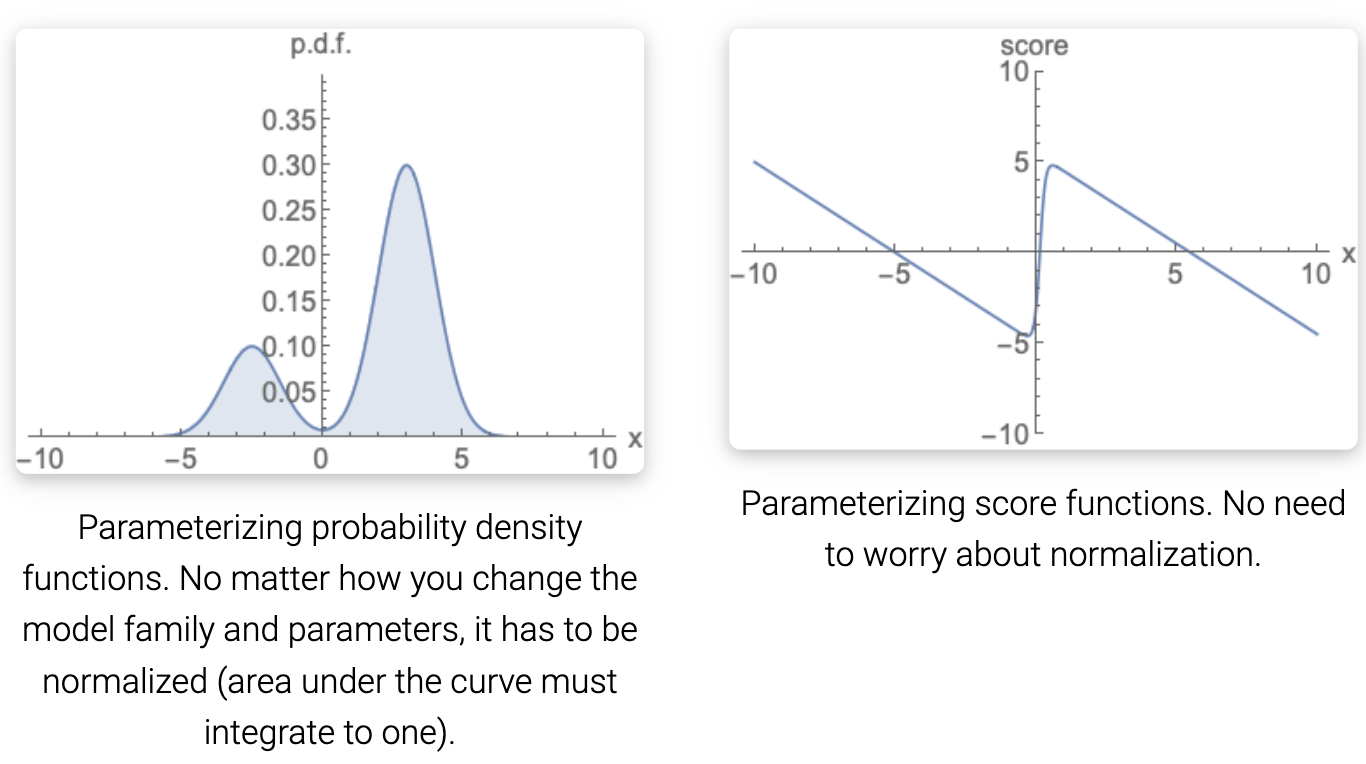
与基于似然的模型相似， 我们可以训练基于分数的模型通过最小化模型和数据分布之间的 Fisher divergence， 定义为：

\(E_{p(x)} [\| \nabla_x \log p(x) - s_\theta(x)\|_2^2]\) 直观地，Fisher散度比较了真实数据分数和基于分数的模型之间的 $\ell_2$ 平方距离。然而，直接计算这种差异是不可行的，因为它需要访问未知的数据分数 $\nabla_x \log p(x)$。 幸运的是，存在一种称为分数匹配的方法，可以在不知道真实数据分数的情况下最小化 Fisher divergence。分数匹配目标可以直接在数据集上估计，并使用随机梯度下降进行优化，类似于训练基于似然模型的对数似然目标(具有已知的归一化常数)。我们可以通过最小化分数匹配目标来训练基于分数的模型，而不需要对抗性优化。

此外，使用分数匹配目标为我们提供了相当大的建模灵活性。Fisher divergence 本身并不要求 $s_\theta(x)$ 是任何归一化分布的实际分数函数，它只是比较真实数据分数和基于分数的模型之间的 $\ell_2$ 距离，对 $s_\theta(x)$ 的形式没有额外的假设。事实上，对基于分数的模型的唯一要求是它应该是一个输入和输出维数相同的向量值函数，这在实践中很容易满足。

作为一个简短的总结，我们可以通过建模它的分数函数来表示一个分布，这个分布可以通过训练一个基于分数的自由形式架构模型来估计。

Langevin dynamics

一旦我们有了训练好的基于分数的模型 $s_\theta(x) \approx \nabla_x \log p(x)$， 我们可以使用叫做郎之万采样的迭代的方式来从中采样。

郎之万采样提供 MCMC 过程以从分布 $p(x)$ 中采样， 仅需使用分数函数 $\nabla_x \log p(x)$。 特别地， 它从一个任意的先验分布 $x_0 \thicksim \pi(x)$ 初始化， 然后用以下方式迭代：

其中 $z_i \thicksim N(0, I)$ 。 当 $\epsilon \rightarrow 0$ 和 $K \rightarrow \infty$， $x_K$ 从上式中得到收敛到从 $p(x)$ 中采样的一个样本。在实践中，当 $\epsilon$ 足够小而 $K$ 足够大时，误差可以忽略不计。

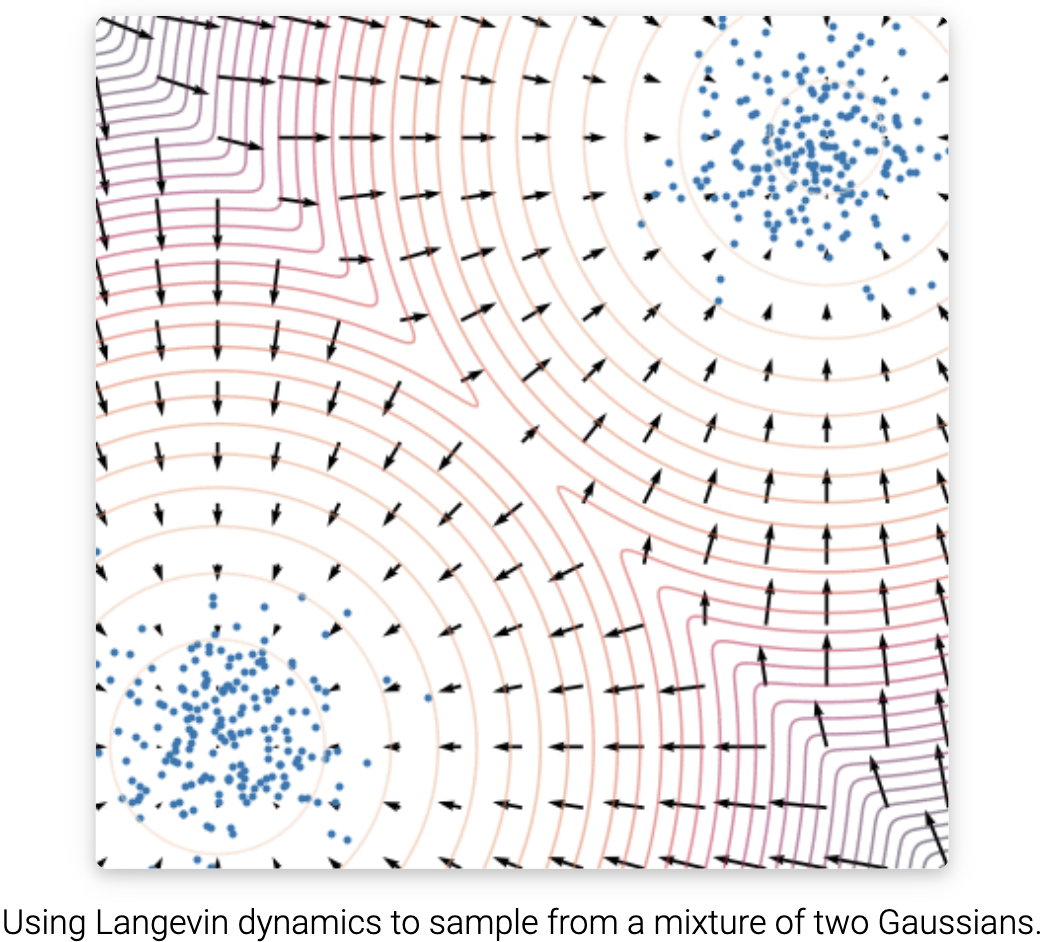
注意到郎之万采样过程 $p(x)$ 仅通过 $\nabla_x \log p(x)$。 因为 $s_\theta(x) \approx \nabla_x \log p(x)$, 我们从基于分数的模型 $s_\theta(x)$ 中产生样本， 通过将其插入上式得到。

Naive score-based generative modeling and its pitfalls

到目前为止，我们已经讨论了如何训练一个基于分数匹配的模型，然后通过朗之万采样生成样本。然而，这种朴素的方法在实践中收效有限，我们将讨论在以往的工作中很少注意到的分数匹配的一些陷阱。

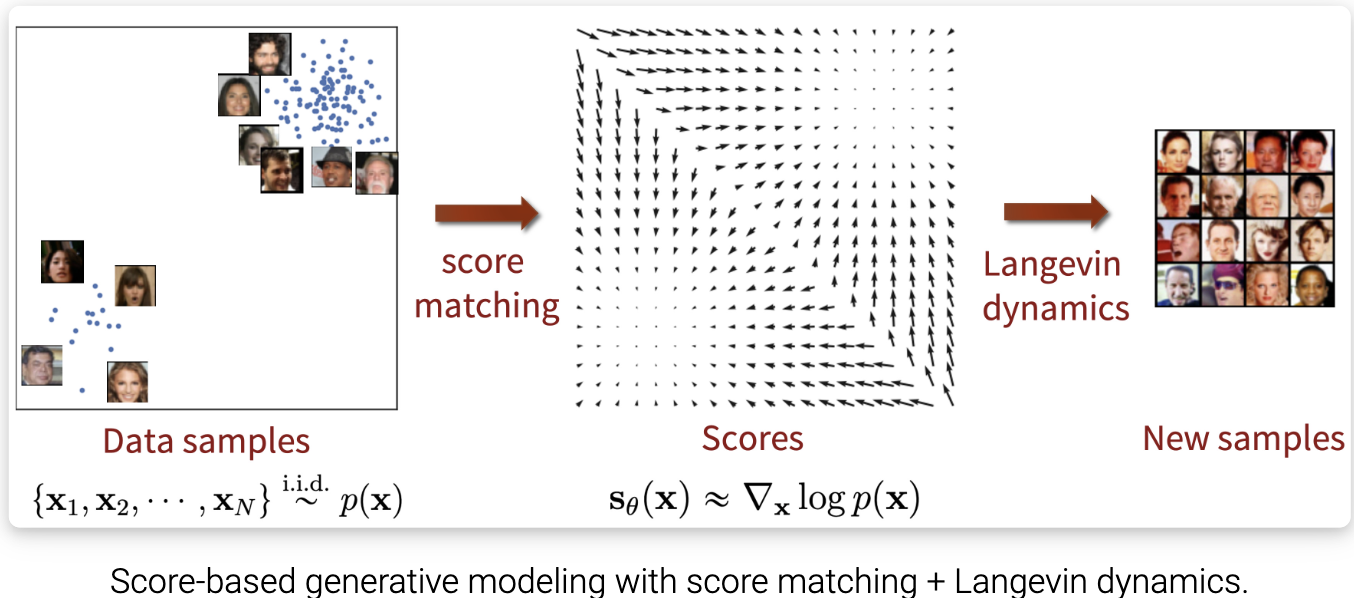
关键的挑战是，在低密度区域，估计的分数函数是不准确的，在低密度区域，很少有数据点可用于计算分数匹配目标。这是预期的分数匹配最小化 Fisher divergence：

\(E_{p(x)} [\| \nabla_x \log p(x) - s_\theta( x)\|_2^2] = \int p(x) \| \nabla_x \log p(x) - s_\theta \|_2^2 dx\) 因为真实数据分数函数和基于分数的模型之间的 $\ell_2$ 差异被 $p(x)$ 加权， 当 $p(x)$ 很小的时候， 低密度区域很大程度上被忽视了。这种行为可能导致低于预期的结果，如下图所示：

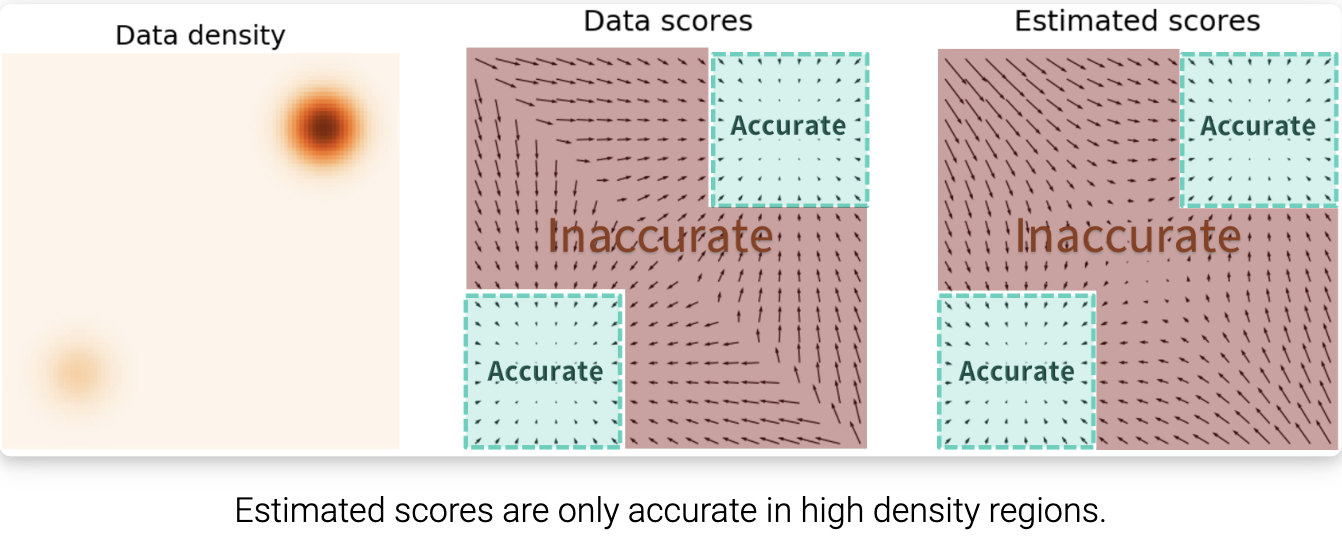
当使用朗之万采样时，当数据位于高维空间时，初始样本极有可能位于低密度区域。因此，拥有一个不准确的基于分数的模型将从程序的一开始就偏离朗之万采样，阻止它生成具有数据代表性的高质量样本。

Score-based generative modeling with multiple noise perturbations

在数据密度低的地区，如何绕过精确评分的困难? 我们的解决方案是用噪声扰动数据点，并在噪声数据点上训练基于分数的模型。当噪声幅度足够大时，它可以填充低数据密度区域，以提高估计分数的准确性。例如，这是当我们扰动两个高斯混合信号时，会发生的情况，这些高斯信号被额外的高斯噪声扰动。

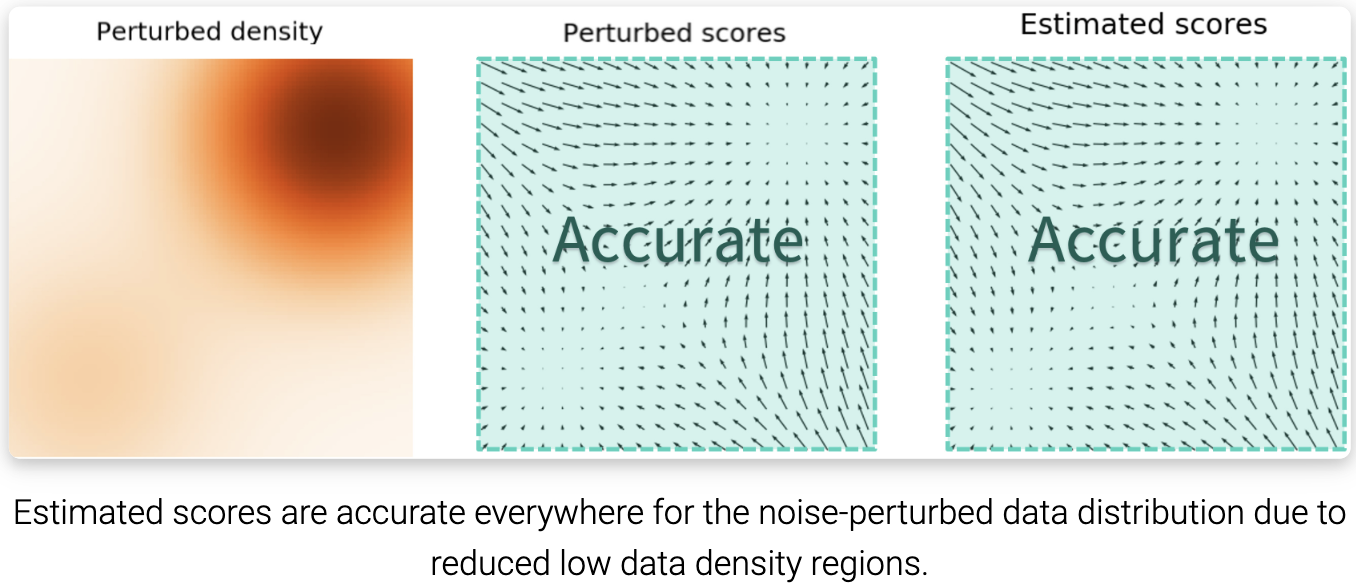
然而，另一个问题仍然存在:我们如何为扰动过程选择一个合适的噪声尺度？ 较大的噪声显然可以覆盖更多的低密度区域，以获得更好的得分估计，但它会过度破坏数据，使其与原始分布发生显著变化。另一方面，较小的噪声对原始数据分布的破坏较小，但不能像我们希望的那样覆盖低密度区域。为了达到两全其美，我们同时使用多个尺度的噪声扰动。假设我们总是用各向同性高斯噪声扰动数据，并让总共有 $L$ 个递增的标准差 $\sigma_1 < \sigma_2 < … < \sigma_L$。 我们首先用每个高斯噪声 $N(0，\sigma_i^2 I)，i=1,2，，L$ 扰动数据分布 $p(x)$ ，得到一个噪声扰动分布。

\(p_{\sigma_i}(x) = \int p(y) N(x; y, \sigma_i^2 I) dy\) 注意我们可以轻易地通过采样 $x \thicksim p(x)$ 和计算 $x + \sigma_i z, z \thicksim N(0, I)$ ， 从 $p_{\sigma_i} (x)$ 采样。

接下来， 我们估计每个噪声扰动分布的分数函数， $\nabla_x \log p_{\sigma_i}(x)$， 用分数匹配通过训练 Noise Conditional Score-Based Model $s_\theta(x, i)$(也叫做 Noise Conditional Score Network，NCSN)， 有:

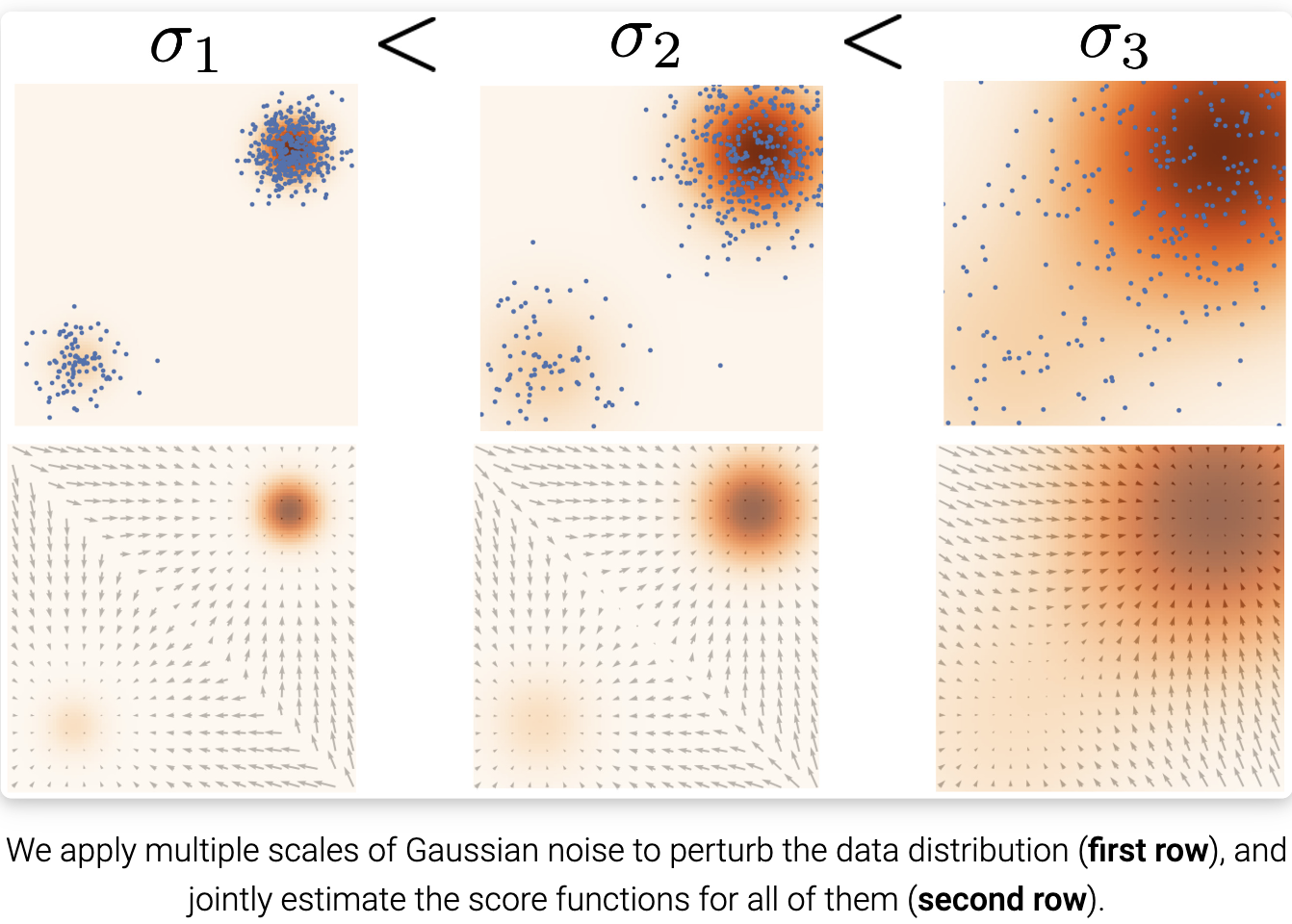
$s_\theta(x, i)$的训练目标是对所有噪声尺度的 Fisher divergences 的加权和：

其中 $\lambda(i) \in R_{>0}$ 是一个正加权函数， 通常被选择为 $\lambda(i) = \sigma_i^2$ 。 上述目标用分数匹配优化， 正如朴素基于分数的模型 $s_\theta(x)$ 的优化。

在训练 noise-conditional score-based model $s_\theta(x, i)$ 后， 对于 $i = L, L -1, …, 1$， 我们可以运行郎之万采样生成样本。这个方法叫做退火郎之万采样， 因为噪声尺度 $\sigma_i$ 随时间递减。

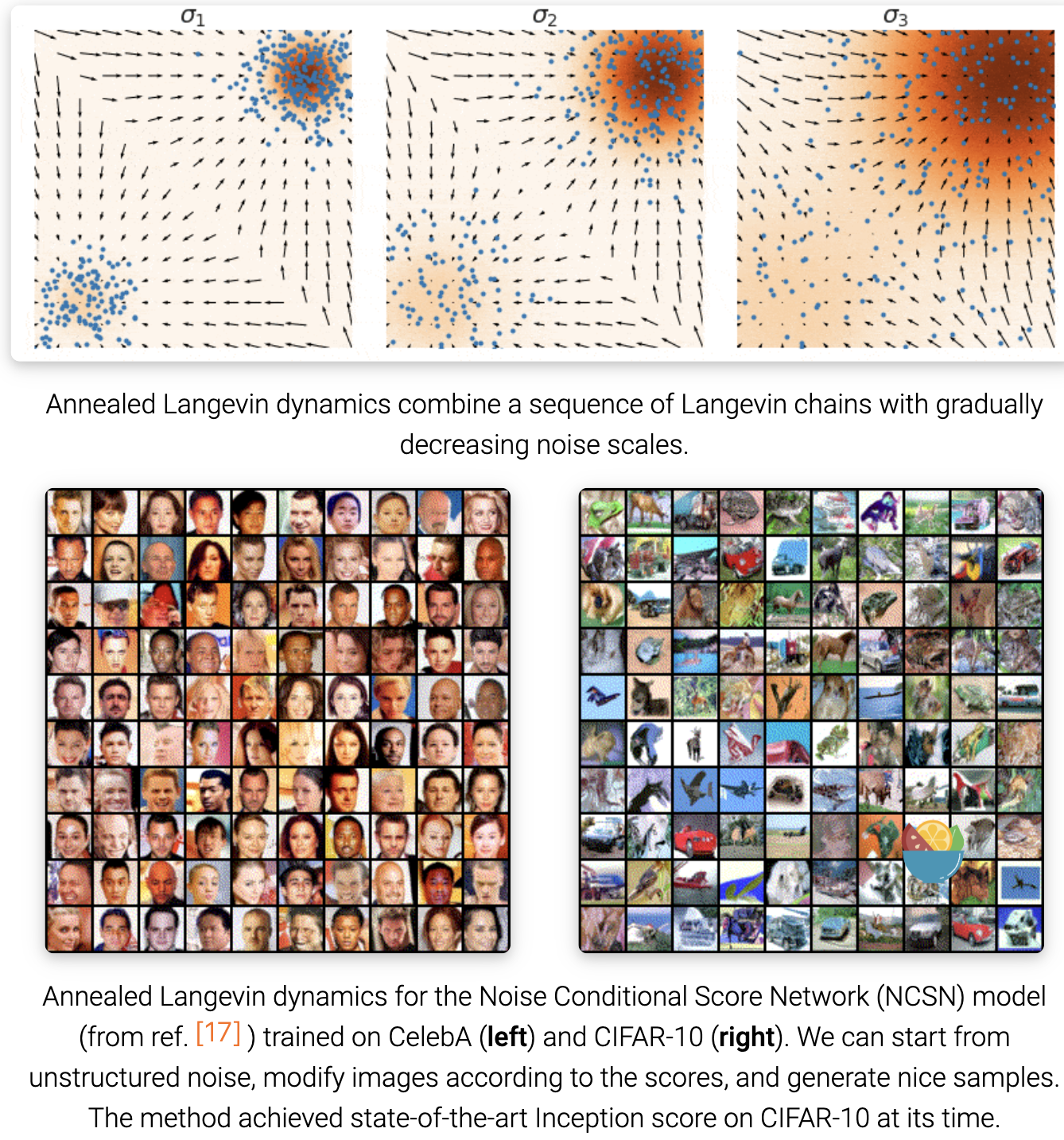
下面是一些实用的建议，用于调整具有多个噪声尺度的基于分数的生成模型：

• 选择 $\sigma_1 < \sigma_2 < … < \sigma_L$ 作为几何级数， $\sigma_1$ 足够小， $\sigma_L$ 可与所有数据点之间的最大成对距离相比较。$L$ 通常是几百或几千的数量级。
• 参数化基于分数的模型 $s_\theta(x, i)$ 用 U-Net 跳跃连接。
• 在测试时使用基于分数的模型的权重上应用指数移动平均

通过这样的最佳实践，我们能够在各种数据集上生成与GANs质量相当的高质量图像样本，如下所示：

Score-based generative modeling with stochastic differential equations (SDEs)

正如我们已经讨论过的，添加多个噪声尺度对于基于分数的生成模型的成功至关重要。通过将噪声尺度的数量推广到无穷大，我们不仅获得了更高质量的样本，而且还获得了精确的对数似然计算，以及用于逆问题求解的可控生成。

Perturbing data with an SDE

当噪声尺度的数量接近无穷大时，我们本质上用不断增长的噪声水平扰乱数据分布。在这种情况下，噪声扰动过程是一个连续时间随机过程，如下所示：

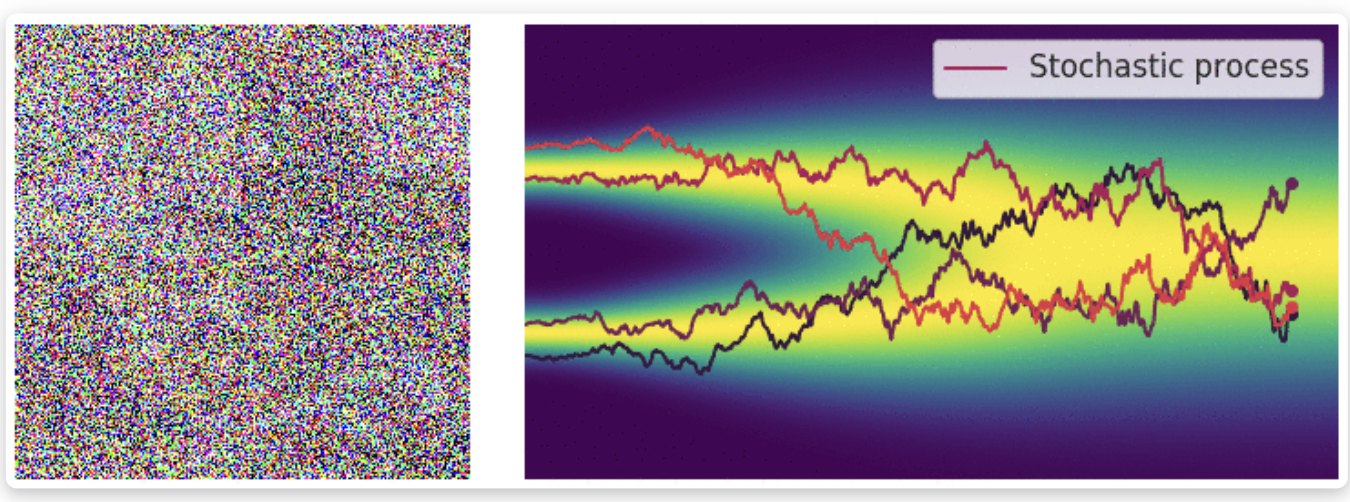
我们如何用简洁的方式表示一个随机过程?许多随机过程(特别是扩散过程)是随机微分方程(SDEs)的解。通常，SDE具有以下形式：

其中 $f(·, t): R^d \rightarrow R^d$ 是一个被叫做漂移系数的 向量-值 函数， $g(t) \in R$ 是一个叫做扩散系数的实值函数， $w$ 表示标准布朗运动， $dw$ 可以视为有限白噪声。随机微分方程的解是随机变量的连续集合 ${x(t)}{t \in [0, T]}$。 随着时间索引 $t$ 从开始时间 $0$ 到结束时间 $t$ 的增长，这些随机变量跟踪随机轨迹。 令 $p_t(x)$ 表示 $x(t)$ 的边缘概率密度函数。 这里 $t \in [0, T]$ 类似于 $i = 1, 2, …, L$ 当我们有偶先数量的噪声尺度， $p_t(x)$ 类似于 $p{\sigma_i}(x)$。显然， $p_0(x) = p(x)$ 是数据分布， 因为在 $t=0$ 时没有扰动施加于数据。 在足够长时间 $T$ 用随机过程扰动 $p(x)$ 后， $p_T(x)$ 变得接近于有迹可循的分布 $\pi(x)$, 叫做先验分布。注意到 $p_T(x)$ 类似于 $p_{\sigma_L}(x)$ 在有限噪声尺度情况下， 其对应于应用最大噪声扰动 $\sigma_L$ 到数据。

等式 8 中的 SDE 是手工设计的， 相似于我们如何手工设计 $\sigma_1 < \sigma_2 < … < \sigma_L$ 在有限噪声尺度的情况下。添加噪声扰动的方法有很多种，SDE的选择并不是唯一的。例如下面的SDE：

用均值为零且方差呈指数增长的高斯噪声扰动数据，这类似于用 $N(0, \sigma_1^2I), N(0, \sigma_2^2I), …, N(0, \sigma_L^2I)$ 当 $\sigma_1 < \sigma_2 < … < \sigma_L$ 几何增长。 因此， SDE 应该被视为模型的一部， 更像 $\sigma_1, \sigma_2, …, \sigma_L$。 我们提供了三种通常对图像工作良好的SDE: Variance Exploding SDE (VE SDE)，Variance Preserving SDE (VP SDE) 和 sub-VP SDE。

Reversing the SDE for sample generation

回想一下，对于有限数量的噪声尺度，我们可以通过退火朗之万采样逆转扰动过程来生成样本，即使用朗之万采样从每个噪声扰动分布中依次采样。对于无限大的噪声尺度，我们可以通过使用反向SDE类似地反转样本生成的扰动过程。

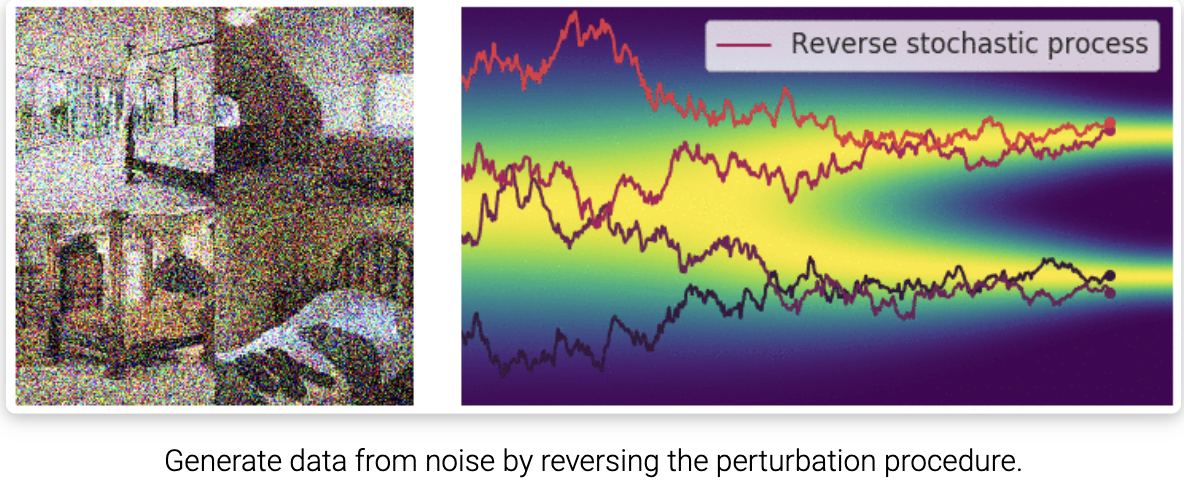
重要的是，任何SDE都有一个对应的反向SDE，其闭式解为：

这里 $dt$ 表示负的无穷小时间步长，因为SDE(10)需要在时间上向后求解(从 $t = T$ 到 $t=0$)。为了计算逆SDE，我们需要估计 $\nabla_x \log p_t(x)$ ，这正是 $p_t(x)$ 的分数函数。

Estimating the reverse SDE with score-based models and score matching

求反向SDE需要知道最终分布 $p_T(x)$， 分数函数为 $\nabla_x \log p_t(x)$。 通过设计， 前者接近于先验分布 $\pi(x)$。 为了估计 $\nabla_x \log p_t(x)$。 我们训练了一个 Time-Dependent Score-Based Model $s_\theta(x, t)$， 因此有： $s_\theta(x, t) \approx \nabla_x \log p_t(x)$。 这类似于用于无穷噪声规模的 noise-conditional score-based model $s_\theta(x, i)$, 训练后有 $s_\theta(x, i) \approx \nabla_x \log p_{\sigma_i}(x)$。

$s_\theta(x, t)$的训练目标是一个连续的 Fisher divergences 的加权组合：

其中 $U(0, T)$ 表示一个在时间间隔 $[0, T]$ 上的均匀分布， 并且 $\lambda: R \rightarrow R_{>0}$ 是一个正加权函数。通常， 我们使用 $\lambda(t) \approx 1 / E[| \nabla_{x(t) \log p(x(t) \mid x(0))} |_2^2] $ 来平衡不同跨时间不同匹配损失的规模。

与以前一样，我们的Fisher散度加权组合可以有效地优化分数匹配方法，如去噪分数匹配和切片分数匹配。 一旦我们的基于分数的模型 $s_\theta(x,t)$ 被训练到最优，我们可以将其插入到(10)中反向SDE的表达式中，以获得估计的反向SDE。

我们可以从 $x(T) \thicksim \pi$, 并且求解上述反向 SDE 来得到一个样本 $x(0)$。 让我们用 $p_\theta$ 表示 $x(0)$ 的分布。 当基于分数的模型 $s_\theta(x, t)$ 训练好， 我们有 $p_\theta \approx p_0$， 在这种情况下 $x(0)$ 是从数据分布 $p_0$ 采样的一个估计样本。

当 $\lambda(t) = g^2(t)$， 我们有 Fisher divergences 的加权组合和 $p_0$ 到 $p_\theta$ 在一些约束条件下的 KL 散度之间的重要联系：

由于这种特殊的联系到KL散度和最小化KL散度和最大化模型训练的似然之间的等价性, 我们叫做 $\lambda(t) = g(t)^2$ 为似然加权函数。使用这种似然加权函数，我们可以训练基于分数的生成模型来实现非常高的似然，与最先进的自回归模型相当，甚至更好。

How to solve the reverse SDE

通过用数值 SDE 求解器求解估计的逆向SDE，我们可以模拟样本生成的逆向随机过程。也许最简单的数值 SDE 求解器是 Euler-Maruyama 方法。当应用于我们估计的反向SDE时，它使用有限时间步长和小高斯噪声离散SDE。具体来说，它选择了一个小的负时间步长 $\Delta t \approx 0$, 初始化 $t \leftarrow T$, 并且遵循以下流程迭代直到 $t \approx 0$:

这里 $z_t \thicksim N(0, I)$。 Euler-Maruyama 方法在性质上与朗之万采样相似，都是通过跟随被高斯噪声扰动的分数函数来更新 $x$。 除了Euler-Maruyama 方法外，其他数值 SDE 求解器可以直接用于求解样本生成的反向SDE，例如Milstein方法和 stochastic Runge-Kutta 方法。我们提供了一个类似于 Euler-Maruyama 的反向扩散求解器，但更适合于求解逆时间 SDE。最近，作者引入了自适应步长SDE求解器，可以更快地生成更好的样本。

此外，我们的反向SDE有两个特殊的性质，允许更灵活的采样方法:

• 通过基于时间的分数模型 $s_\theta(x,t)$，我们得到了 $\nabla_x \log p_t(x)$ 的估计值。
• 我们只关心每个边缘分布的抽采样 $p_t(x)$。 不同时间步长的样本可以有任意的相关性，不必形成从反向SDE中采样的特定轨迹。

由于这两个性质的结果，我们可以应用 MCMC 方法来微调从数值SDE求解器获得的轨迹。具体地说，我们提出了 Predictor-Corrector samplers。 predictor 可以是从现有样本中预测 $x(t + \Delta t) \thicksim p_t+ \Delta t(x)$ 的任意数值SDE求解器。 corrector 可以是任何 MCMC 程序，只依赖于分数函数，如朗之万采样和 Hamiltonian Monte Carlo。

在 Predictor-Corrector sampler 的每一步中，我们首先使用 predictor 选择适当的步长 $\Delta t < 0$， 然后基于当前采样 $x(t)$ 预测 $x(t + \Delta t)$。接下来， 我们运行几个 corrector 步骤根据我们的基于分数的模型 $s_\theta(x, t + \Delta t)$ 提升采样 $x(t + \Delta t)$， 以便 $x(t + \Delta)$ 变成一个从 $p_{t + \Delta t}(x)$更高质量的样本。

通过 Predictor-Corrector 方法和基于分数的模型的更好架构，我们可以在CIFAR-10上实现最先进的样本质量(以FID和Inception分数衡量)，优于迄今为止最好的GAN模型(StyleGAN2 + ADA)。

采样方法对于高维数据也是可扩展的。例如，它可以成功地生成高分辨率 $1024 \times 1024$ 的高保真图像。

Probability flow ODE

尽管能够生成高质量的样本，基于Langevin MCMC 和 SDE 求解器的采样器并没有提供一种方法来计算基于分数的生成模型的精确对数似然值。下面，我们将介绍一个基于常微分方程(ODE)的采样器，它允许精确的似然计算。

我们证明转换任何 SDE 为常微分方程(ODE)而不改变其边缘分布 ${p_t(x)}_{t \in [0, T]}$ 是可能的。 因此，通过求解这个ODE，我们可以从与反向SDE相同的分布中取样。SDE 对应的 ODE 称为 probability flow ODE：

\(dx = [f(x, t) - \frac{1}{2} g^2(t) \nabla_x \log p_t(x)] dt \tag{14}\) 下图描述了 SDE 和 probability flow ODE 的轨迹。虽然ODE轨迹明显比SDE轨迹更平滑，但它们将相同的数据分布转换为相同的先验分布，反之亦然，共享相同的边缘分布 ${p_t(x)}_{t \in [0, T]}$。 换句话说，通过求解 probability flow ODE 得到的轨迹与 SDE 轨迹具有相同的边缘分布。

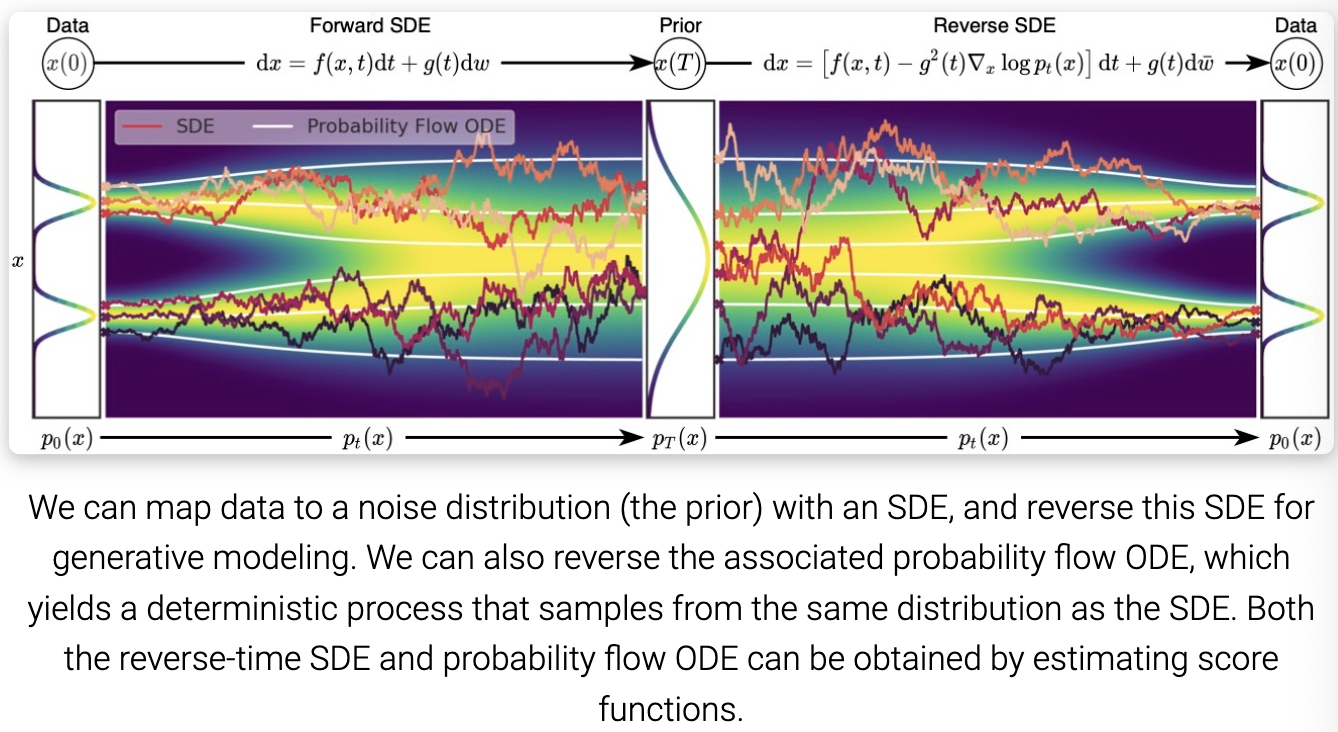
这种 probability flow ODE 公式有几个独特的优点。

当 $\nabla_x \log p_t(x)$ 被它的估计 $s_\theta (x, t)$ 替换后， probability flow ODE 变成 probability flow ODE 的一个特殊例子。特别地，它是 continuous normalizing flows 的一个例子， 因为 probability flow ODE 将数据分布 $p_0(x)$ 转换为先验噪声分布 $p_T(x)$ (因为它与SDE共享相同的边际分布)并且完全可逆。

因此，probability flow ODE 继承了 neural ODE 或 continuous normalizing flows 的所有属性，包括精确的对数似然计算。具体来说，我们可以利用 instantaneous change-of-variable formula，用数值 ODE 求解器从已知先验密度 $p_T$ 计算未知数据密度 $p_0$。

事实上，即使没有最大似然训练，我们的模型也能在 uniformly dequantized 的CIFAR-10图像上实现最先进的对数似然。

当我们用之前讨论过的似然加权训练基于分数的模型，并使用变分去量化来获得离散图像上的似然时，我们可以获得与最先进的自回归模型相当甚至更好的似然(都没有任何数据增强)。

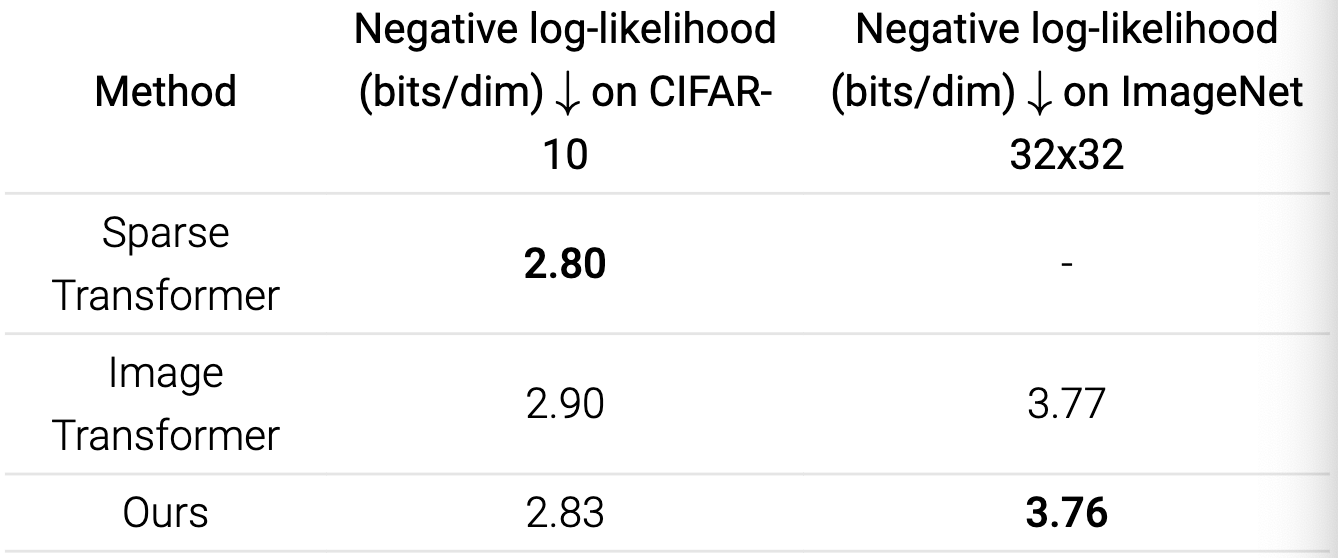
Controllable generation for inverse problem solving

基于分数的生成模型特别适合解决逆问题。逆问题本质上与贝叶斯推理问题相同。设 $x$ 和 $y$ 是两个随机变量，假设我们知道从 $x$ 生成 $y$ 的正向过程，用转移概率分布表示 $p(y \mid x)$。 逆问题就是计算 $p(x \mid y)$。 利用贝叶斯规则，有： $p(x \mid y) = p(x)p(y \mid x) / \int p(x) p(y \mid x) dx$。 这个表达式可以通过在两边取关于 $x$ 的梯度来大大简化，从而得到以下关于分数函数的贝叶斯规则：

通过分数匹配，我们可以训练一个模型来估计无条件数据分布的分数函数，即 $s_\theta(x) \approx \nabla_x \log p(x)$。这将使我们能够通过等式 15 轻松地从已知前向过程 $p(y \mid x)$ 计算后验分数函数 $\nabla_x \log p(x \mid y)$， 并且从中用郎之万采样。

德克萨斯大学奥斯汀分校最近的一项工作表明，基于分数的生成模型可以应用于解决医学成像中的逆问题，例如加速磁共振成像(MRI)。同时，我们不仅在加速MRI上，而且在稀疏视图计算机断层扫描(CT)上证明了基于分数的生成模型的优越性能。我们能够获得与监督式或展开式深度学习方法相当甚至更好的性能，同时在测试时对不同的测量过程更加健壮。

下面我们将展示一些求解计算机视觉逆问题的例子。

Connection to diffusion models and others

自2019年以来，我开始研究基于分数的生成建模，当时我正在努力使分数匹配可扩展，以便在高维数据集上训练基于深度能量的模型。我在这方面的第一次尝试导致了 sliced score matching 。 尽管 sliced score matching 对于训练基于能量的模型具有可扩展性，但令我惊讶的是，即使在MNIST数据集上，从这些模型中进行郎之万采样也无法产生合理的样本。我开始调查这个问题，发现了三个关键的改进，可以产生非常好的样本:(1)多个噪声尺度的扰动数据，并为每个噪声尺度训练基于分数的模型;(2)使用U-Net架构(我们使用了RefineNet，因为它是U-Net的现代版本)用于基于分数的模型; (3)将郎之万 MCMC应用于各个噪声尺度，并将它们链接在一起。通过这些方法，我能够在CIFAR-10上获得最先进的Inception评分(甚至比最好的GANs还要好!)，并生成分辨率最高的高保真图像样本。

然而，用多个尺度的噪声干扰数据的想法绝不是基于分数的生成模型所独有的。它以前已经被用于，例如，模拟退火，退火的重要性抽样，扩散概率模型，infusion training，和生成随机网络的变分回溯。在所有这些工作中，扩散概率建模可能是最接近基于分数的生成建模。扩散概率模型是Jascha和他的同事在2015年首次提出的分层隐变量模型，它通过学习变分解码器来生成样本，以逆转将数据扰动为噪声的离散扩散过程。在没有意识到这项工作的情况下，基于分数的生成建模被提出并从一个非常不同的角度独立地进行。尽管都是多尺度噪声扰动数据，但基于分数的生成建模和扩散概率建模之间的联系在当时似乎很肤浅，因为前者是通过分数匹配训练并由朗之万采样，而后者是通过变分下界(ELBO)训练并使用学习解码器采样。

2020年，Jonathan Ho及其同事显著改善了扩散概率模型的经验性能，并首次揭示了与基于分数的生成建模的更深层次的联系。他们表明，用于训练扩散概率模型的ELBO本质上等同于基于分数的生成建模中使用的分数匹配目标的加权组合。此外，通过将解码器参数化为具有U-Net架构的基于分数的模型序列，他们首次证明了扩散概率模型也可以生成与GANs相当或更好的高质量图像样本。

受他们工作的启发，我们在ICLR 2021年的一篇论文中进一步研究了扩散模型和基于分数的生成模型之间的关系。我们发现，扩散概率模型的采样方法可以与基于分数的模型的退火朗之万采样集成，以创建一个统一的、更强大的采样器(预测-校正抽样器)。通过将噪声尺度的数量推广到无穷大，我们进一步证明了基于分数的生成模型和扩散概率模型都可以被视为由分数函数决定的随机微分方程的离散化。这项工作将基于分数的生成建模和扩散概率建模连接到一个统一的框架中。

总的来说，这些最新的发展似乎表明，基于分数的生成建模与多个噪声扰动和扩散概率模型是同一模型家族的不同角度，就像波力学和矩阵力学是物理学历史上量子力学的等效公式一样。分数匹配和基于分数的模型的视角允许人们准确地计算对数可能性，自然地解决逆问题，并直接连接到基于能量的模型，Schrödinger桥梁和最优运输。扩散模型的视角自然地与VAEs、有损压缩联系在一起，可以直接与变分概率推理结合在一起。本文主要介绍第一个视角，但我强烈建议感兴趣的读者也了解扩散模型的另一种视角(参见Lilian Weng的一篇很棒的博客)。

最近关于基于分数的生成模型或扩散概率模型的许多工作都受到了双方研究知识的深刻影响(参见牛津大学研究人员策划的网站)。尽管基于分数的生成模型和扩散模型之间有着深刻的联系，但很难为它们都属于的模型家族提出一个总括性术语。DeepMind的一些同事提议将其称为生成扩散过程。未来是否会被社区采用还有待观察。

Reference

1.Generative Modeling by Estimating Gradients of the Data Distribution

• Previous
  【深度学习】Hungarian loss：End-to-end people detection in crowded scenes
• Next
  【深度学习】What are Diffusion Models?