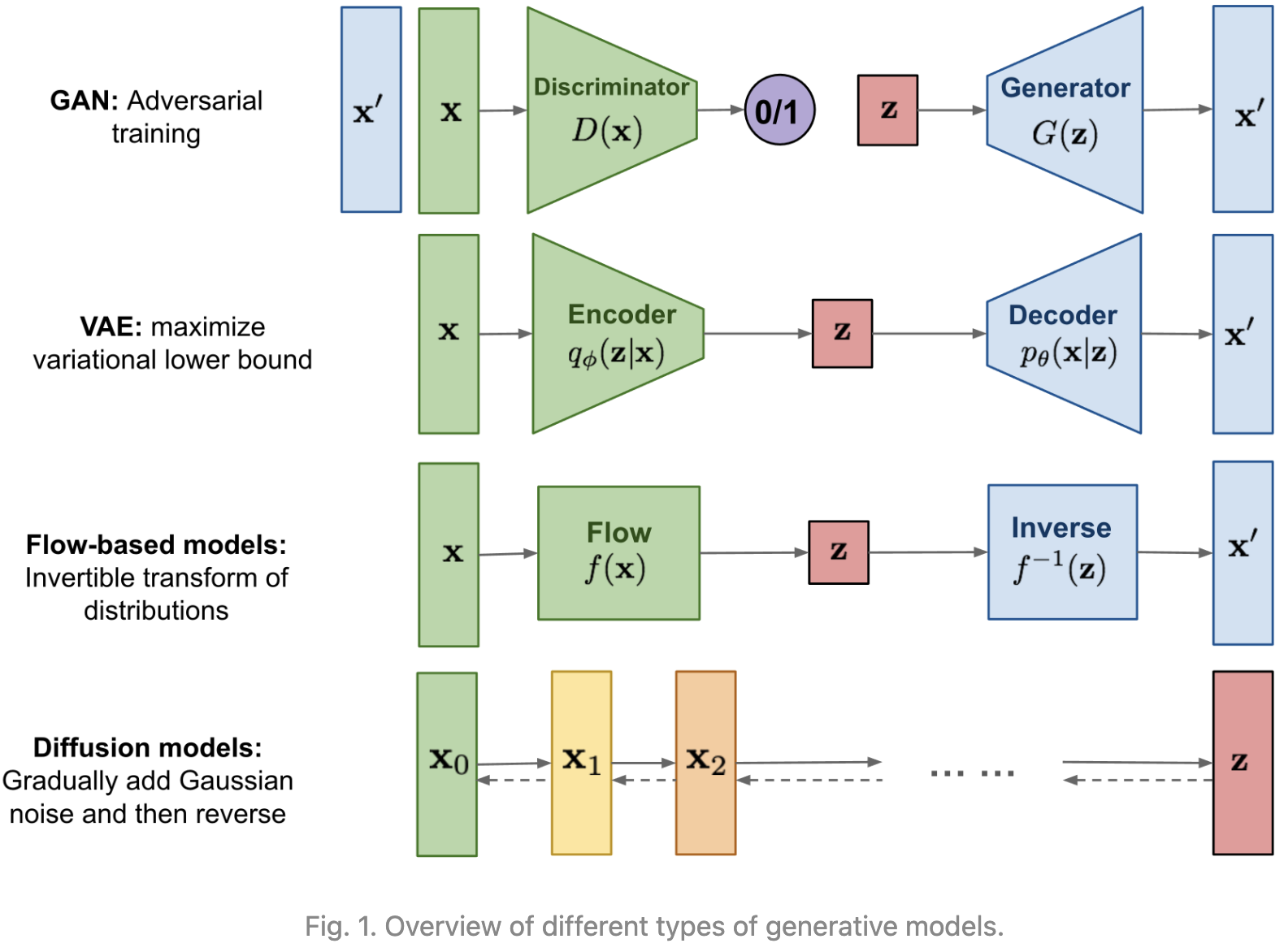
GAN模型因潜在的不稳定训练和由于其对抗性训练性质而产生的较少多样性而闻名。VAE依赖代理损失。Flow 模型必须使用专门的结构来构造可逆变换。
扩散模型的灵感来自于非平衡热力学。他们定义了一个扩散步骤的马尔可夫链,慢慢地向数据添加随机噪声,然后学习反向扩散过程,从噪声中构建所需的数据样本。与 VAE 或 Flow 模型不同,扩散模型的学习过程是固定的,隐变量具有高维数(与原始数据相同)。
What are Diffusion Models?
已经提出了一些基于扩散的生成模型,其中包括diffusion probabilistic models(Sohl-Dickstein et al., 2015),noise-conditioned score network(NCSN;Yang & Ermon, 2019),以及 denoising diffusion probabilistic models (DDPM;Ho et al. 2020)。
Forward diffusion process
给定一个从真实数据分布中抽样的数据点 $x_0 \thicksim q(x)$, 让我们定义一个正向扩散过程,在这个过程中,我们分 $T$ 步向样本中添加少量的高斯噪声,产生一个噪声样本 $x_1,,x_T$ 序列。步长由方差表 ${\beta_t \in (0,1)}_{t=1}^T$ 控制。
\[q(x_t \mid x_{t-1}) = N(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I) \quad q(x_{1:T} \mid x_0) = \prod_{t=1}^T q(x_t \mid x_{t-1})\]随着步长 $t$ 变大,数据样本 $x_0$ 逐渐失去其可区分的特征。最终, 当 $T \rightarrow \infty$, $x_T$ 等价于一个各向同性的高斯分布。
上述过程有一个有一个好的性质, 我们可以用重参数技巧在任意时间步 $t$ 采样 $x_t$。 令 $\alpha_t = 1 - \beta_t$, $\bar \alpha_t = \prod_{i=1}^t \alpha_i$:
\[\begin{align} x_t &= \sqrt{\alpha_t} x_{t-1} + \sqrt{1 - \alpha_t} \epsilon_{t-1} \\ &= \sqrt{\alpha_t \alpha_{t-1}}x_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar \epsilon_{t-2} \\ &= ... \\ &= \sqrt{\bar \alpha_t} x_0 + \sqrt{1 - \bar \alpha_t} \epsilon \end{align}\] \[q(x_t \mid x_0) = N(x_t; \sqrt{\bar \alpha_t}x_0, (1- \bar \alpha_t) I)\]其中 $\epsilon_{t-1}, \epsilon_{t-2}, …, \thicksim N(0,1)$, $\bar \epsilon_{t-2}$ 合并两个高斯分布。回忆当我们融合两个不同方差的高斯分布, $N(0, \sigma_1^2 I)$ 和 $N(0, \sigma_2^2 I)$, 新的分布是 $N(0, (\sigma_1^2 + \sigma_2^2)I)$。 这里融合的标准差为 $\sqrt{(1 - \alpha_t) + \alpha_t(1 - \alpha_{t-1})} = \sqrt{1 - \alpha_t \alpha_{t-1}}$。
通常,当样本变得嘈杂时,我们可以承担更大的更新步骤,所以 $\beta_1 < \beta_2 < … < \beta_T$, 因此 $\bar \alpha_1 > …. > \bar \alpha_T$。
Connection with stochastic gradient Langevin dynamics
朗之万动力学是物理学的一个概念,用于分子系统的统计建模。与随机梯度下降相结合,随机梯度朗之万动力学(Welling & Teh 2011)可以从概率密度 $p(x)$ 中生成样本,只使用马尔科夫更新链中的梯度 $x \log p(x)$ :
\(x_t = x_{t-1} + \frac{\delta}{2} \nabla_x \log q(x_{t-1}) + \sqrt{\delta} \epsilon_t, \quad \epsilon_t\thicksim N(0, I)\) 其中 $\delta$ 是步长。 当 $T \rightarrow \infty, \epsilon \rightarrow 0$, $x_T$ 等于真实概率密度 $p(x)$。
与标准SGD相比,随机梯度朗之万动力学在参数更新中注入了高斯噪声,以避免崩溃到局部极小值。
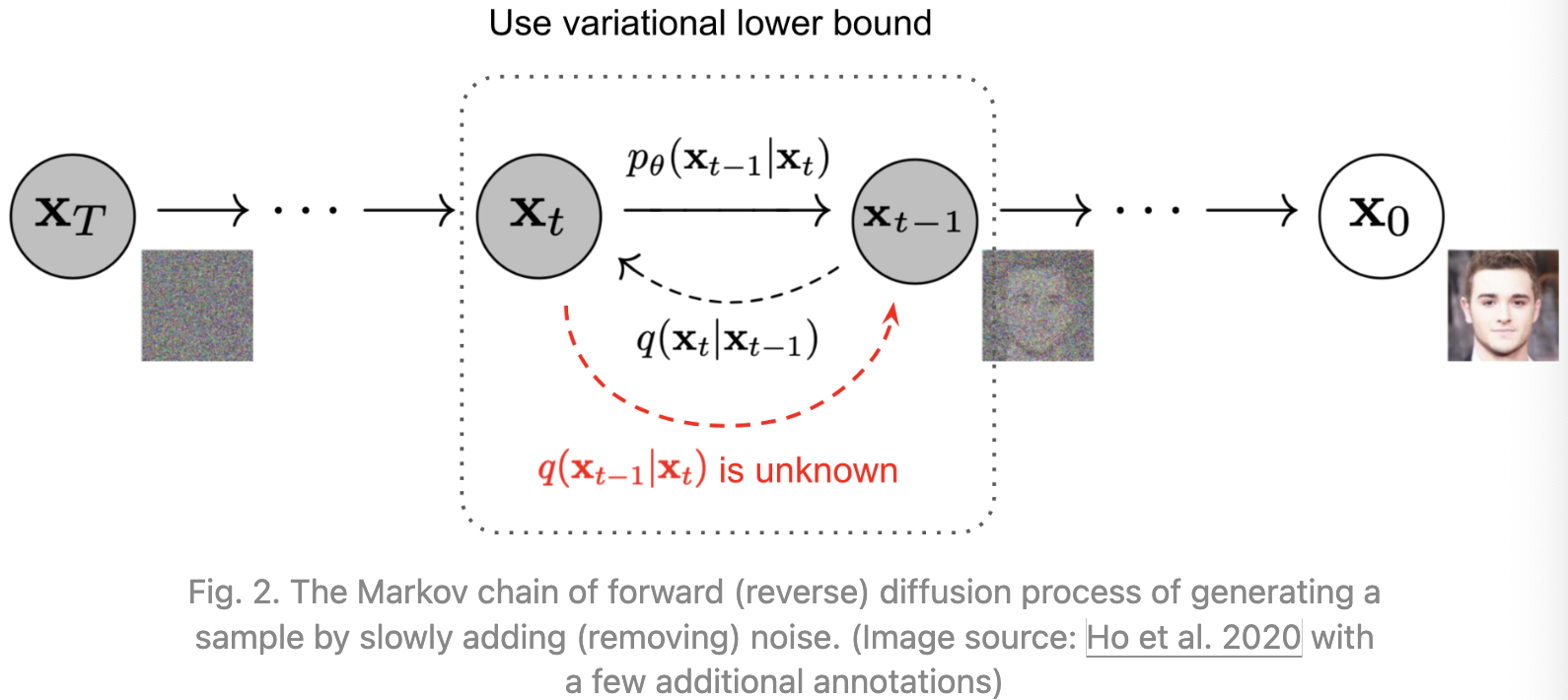
Reverse diffusion process
如果我们能将上述过程反转, 并且从 $q(x_{t-1} \mid x_t)$ 采样, 我们将能够从高斯噪声输入中重建真实的样本 $x_T \thicksim N(0, I)$。 注意 $\beta_t$ 足够小, $ q(x_{t-1} \mid x_t)$ 将是高斯分布。不幸的是, 我们不能直接估计 $q(x_{t-1} \mid x_t)$ , 因为它需要使用整个数据集, 因此我们需要学习一个模型 $p_\theta$ 估计这些条件概率以便运行逆扩散过程:
\[p_\theta(x_{0:T}) = p(x_T)\prod_{t=1}^T p_\theta(x_{t-1} \mid x_t)\]Reference
-
Previous
【深度学习】Generative Modeling by Estimating Gradients of the Data Distribution -
Next
【深度学习】Robust Compressed Sensing MRI with Deep Generative Priors