Abstract
由于其作为生成模型的强大性能,扩散模型最近在社区中引起了极大的兴趣。
此外,它对逆问题的应用已经证明了最先进的性能。
不幸的是,扩散模型有一个关键的缺点——它们本质上采样速度很慢,需要几千个迭代步骤才能从纯高斯噪声中生成图像。
在这项工作中,我们表明从高斯噪声开始是不必要的。
相反,从具有更好初始化的单个正向扩散开始,显著减少了反向条件扩散中的采样步骤数量。
这种现象被正式解释为随机差分方程的 contraction 理论,例如我们的条件扩散策略——反向扩散的交替应用,然后是 non-expansive data consistency 步骤。
被称为 Come-Closer-Diffuse-Faster(CCDF)的新采样策略也揭示了关于逆问题现有前馈神经网络方法如何与扩散模型协同结合的新见解。
超分辨率、图像绘画和压缩感知 MRI 的实验结果表明,我们的方法可以在显著减少采样步骤的情况下实现最先进的重建性能。
Background
Score-based Diffusion Models
Discrete Forms of SDEs
Main Contribution
The CCDF Algorithm
我们的CCDF加速方案的目标是使反向扩散从 $N′ := N_{t0} < N$ 开始,以便可以显著减少反向扩散步数。为此,我们的CCDF算法由两个步骤组成:向前扩散到 $N′$,具有更好的初始化 $x_0$,然后是反向条件扩散到 $i = 0$。
具体来说,对于给定的初始估计 $x_0$,正向扩散过程可以通过单步扩散执行,如下所示:
\[x_{N'} = a_{N'} x_0 + b_{N'} z \tag{12}\]$z \thicksim N(0, I)$, 并且 $a_{N’}, b_{N’}$ 对于 SMLD 和 DDPM 可以使用 (10) 和 (5) 分别对每个扩散模型计算。
至于条件扩散模型, SRdiff 和 SR3 是用于超分辨的特殊例子, 其将低分辨图像拼接作为输入。然而,这些方法试图重新设计分数函数,以便可以从条件分布中采样,从而导致一个非常复杂的公式。
相反,我们在这里提出了一个更简单但有效的条件扩散。具体来说,我们的反向扩散使用标准的反向扩散,与强制数据一致性的操作交替进行:
\[x_{i-1}' = f(x_i, i) + g(x_i, i) z_i \tag{13}\] \[x_{i-1} = A x_{i-1}' + b\]其中 $f(x_i, i)$ 和 $g(x_i, i)$ 依赖于扩散模型的类型(见表1), $z_i \thicksim N(0, I)$, 并且 $A$ 是 non-expansive mapping:
\[\| Ax - Ax' \| \leq \| x - x \|, \qquad \forall x, x' \tag{15}\]特别地, 我们假设 $A$ 是线性的。
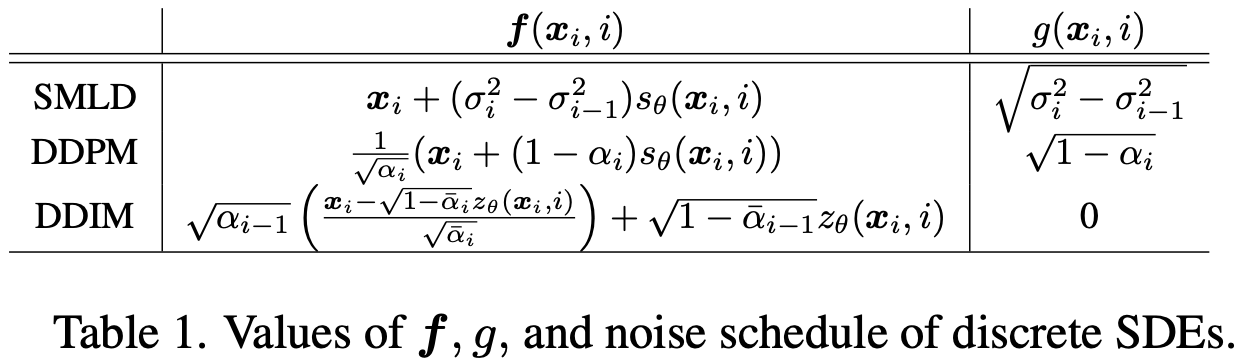
## Fast Convergence Principle of CCDF
现在,我们准备展示为什么 CCDF 提供的收敛速度比从高斯噪声开始的标准条件扩散模型快得多。事实上,关键的创新来自于数学发现,即虽然正向扩散增加了估计误差,但条件反向扩散以指数速度将其降低得更快。因此,我们可以找到一个“sweet spot” $N′$,使得正向扩散到 $N′$,然后是反向扩散,可以显著减少初始估计 $x_0$ 的估计误差。这种快速收敛原理显示在以下定理中,其证明可以在补充材料中找到。首先,以下引理是高斯噪声独立性的一个简单结果。
Lemma 1. 令 $\tilde x_0 \in R^n$ 和 $x_0 \in R^n$ 分别表示真实的干净的图像和初始估计, 并且初始估计误差表示为 $\epsilon_0 = | x_0 = \tilde x_0 |^2$。 此外,假设 $x_{N′}$ 和 $x_{\tilde N′}$ 分别表示从 $x_0$ 和 $\tilde x_0$ 前向扩散,使用(12)。然后,前向扩散后的估计误差由:
\[\bar \epsilon_{N'} := E \| x_{N'} - \tilde x_{N'}\|^2 \ \\ = a_{N'}^2 \epsilon_0 + 2b_{N'}^2 n \tag{16}\]现在,以下定理是我们证明的关键步骤,来自随机差分方程的随机 contraction 性质:
Theorem 1. 使用 (13) 和 (14) 考虑反向扩散, 我们有:
\[\bar \epsilon_{0, r} \leq \frac{2 C_{\tau}}{1 - \lambda^2} + \lambda^{2N'} \bar \epsilon_{N'} \tag{17}\]其中 $\bar \epsilon_{0, r}$ 表示反向条件扩散路径到 $i=0$ 的估计的误差, 并且 $\tau = \frac{Tr(A^\top A)}{n}$。此外,收缩率 $\lambda$ 和常数 $C$ 具有以下闭式表达式:
\[\lambda = \begin{cases} \max_{i \in [N']} \sqrt{\alpha_i}(\frac{1 - \bar \alpha_{i-1}}{1 - \bar \alpha_i}) \qquad (DDPM) \\ \max_{i \in [N']} \frac{\sigma_{i-1}^2 - \sigma_0^2}{\sigma_i^2 - \sigma_0^2} \qquad (SMLD) \\ \max_{i \in [N']} \frac{\sigma_{i-1}}{\sigma_i} \qquad (DDIM) \tag{18} \end{cases}\]现在我们有了显示加速捷径存在的主要结果。
Theorem 2 (Shortcut path) 对于任意 $0 < \mu \leq 1$, 存在一个最小值 $N’ (= t_0N < N)$, 使得 $\bar \epsilon_{0, r} \leq \mu \epsilon_0$。 此外, 只要 $\epsilon_0$ 变小, $N’$ 减小。
Theorem 1 说明条件反向扩散是指数 contracting 的。 然后 ,Theorem 2 告诉我们可以使用更短的采样路径获得更好的结果。因此,我们没有必要从 $N$ 开始采样。我们可以从任意的时间步 $N′ < N$ 开始,并且仍然更快地收敛到在 $N$ 开始采样程序时可以实现的相同点。此外,由于我们有更好的初始化,使 $\epsilon_0$ 更小,那么我们需要更小的反向扩散步,实现更高的加速。
例如,我们可以使用预训练的神经网络 $G_{\psi}$ 初始化损坏的图像,该网络已广泛应用于不同的任务[16,39,40]。这些方法的计算速度通常非常快,因此不会引入额外的计算过载。使用这个相当简单和快速的修复,我们观察到我们能够选择较小的 $t_0$ 值,具有更稳定的表现。例如,在核磁共振重建的情况下,我们可以选择小至 $0.02$ 的 $t0$ ,同时以50倍的加速优于 score-MRI [6]。
-
Previous
【深度学习】SNIPS: Solving Noisy Inverse Problems Stochastically -
Next
【深度学习】Score-based diffusion models for accelerated MRI