Abstract
评估重建的高光谱图像(HSI)的质量对恢复和超分辨率具有重要意义。
目前的图像质量评估方法,如峰值信号噪声比,需要原始参考图像的可用性,这在现实中通常不可用。
在本文中,我们提出了一种基于 quality-sensitive features extraction 的无参考高光谱图像质量评估。
在光谱和空间域分析原始和扭曲的HSI之间的统计属性差异,然后提取对图像质量敏感的多个统计特征。
通过结合所有这些统计特征,我们从原始的高光谱数据集中学习了一个多元高斯(MVG)模型作为基准。
为了评估重建的 HSI 的质量,我们将其划分为不同的局部块,并在每个块上拟合一个MVG模型。
计算了每个重建的 HSI 块的 MVG 模型和基准 MVG 模型之间的修改后的 Bhatacharyya 距离,以测量质量。
最终的质量分数是通过所有块的平均池化获得的。
我们使用我们提出的方法评估了机载可见红外成像光谱仪(AVIRIS)和 Hyperspec-VNIR-C(HyperspecVC)数据的五种最先进的超分辨率方法。
经证实,所提出的质量评分与当前基于参考的评估指数一致,这表明了所提出的无参考图像质量评估方法的有效性和潜力。
Introduction
具有丰富的场景空间和光谱信息的高光谱图像(HSI)在许多领域非常有用,如矿产开采、农业和环境管理[1-3]。由于空间分辨率有限,为了提高获得的HSI的质量,超分辨率是一种重要的增强技术[4-12]。为了评估重建的高分辨率HSI,传统策略是通过下采样将原始数据降级为更粗的分辨率。然后,将原始数据用作参考图像,并与重建的高分辨率图像进行比较。缺点是,由于无法保证超分辨率性能对缩放变化的不变性,超分辨率方法在原始数据上的性能可能不如下采样数据[13,14]。虽然在原始数据而不是下采样数据上评估超分辨率方法自然更好,但如果将超分辨率应用于原始数据,则无法评估参考图像。
据我们所知,没有关于 HSI 重建的无参考质量评估的出版工作。Alparone等人在[14]中提出了一种无参考全色图像评估方法,其需要高分辨率全色图像来评估重建的多光谱图像。此方法不适用于全色图像不可用的情况。还有其他一些为彩色图像设计的无参考图像评估方法[15-17],但它们不能直接应用于高光谱图像。这些方法只能评估空间质量,并给出反映人类主观视觉感的质量分数。此外,它们不能处理光谱保真度,这对HSI的解释很重要。
在这项研究中,我们为HSI提出了一种无参考质量评估方法。HSI具有一些对失真敏感的统计特性,这些统计数据与常规统计数据的偏差反映了失真程度。这些统计数据可以作为质量敏感特征提取。通过分析原始和失真的HSI的统计属性,我们提取了光谱和空间领域的多个质量敏感特征。在整合所有这些特征后,我们可以从原始的高光谱训练数据集中学习这些特征的多元高斯模型(MVG)。学习的MVG被视为与在重建的HSI上的MVG模型进行比较的基准。两个MVG模型之间的距离被计算为质量测量,高值代表低质量。为了应用这种方法,我们将重建的HSI划分为不同的局部块,并测量每个局部块的图像质量。重建的HSI的最终质量分数是通过平均池化获得的。
我们在本文中考虑了四项贡献。首先,我们提出了高光谱图像的第一个无参考评估方法。我们的方法不需要任何参考图像或对原始图像进行下采样,这非常适合实际应用。其次,为了利用光谱和空间信息进行质量评估,除了现成的空间特征外,我们分析了光谱域的统计特性,为光谱域设计了质量敏感的特征,并将其与空间特征相结合,形成一个联合的光谱-空间质量敏感特征向量。第三,与当前的彩色图像评估方法相比,我们的方法也可以盲评估光谱保真度。最后,我们通过在几个真实的HSI上进行测试来验证我们的方法作为HSI评估工具的潜力,这些HSI由最先进的超分辨率方法重建。
本文的其余部分组织如下。在第2节中,我们分析了HSI的统计属性,并提取了质量敏感的特征。计算质量分数的方法在第3节中给出。我们分别在第4节和第5节中介绍实验结果并讨论实验结果。我们在第6节中得出结论。
Quality-Sensitive Statistics Features
图像拥有因失真而偏离常规图像的统计数据,将这些统计数据提取为特征并测量其偏差,因此可以在没有任何参考的情况下评估HSI[17]。以前为彩色图像设计的质量敏感统计特征主要集中在空间域[18-22]。 为了利用HSI的光谱相关性,我们还需要从光谱域中提取质量敏感的特征。在本节中,我们首先分析光谱域的统计属性,并设计了一种质量敏感的光谱特征提取方法。然后,我们证明现有的空间特征对HSI是有效的。通过整合我们提出的光谱特征和空间特征,我们形成了一个联合的光谱-空间质量敏感特征向量。
Statistics Features in Spectral Domain
在本小节中,在分析光谱域中的统计数据后,提出了对光谱质量敏感的特征。我们观察到,原始 HSI 的局部归一化光谱将遵循高斯分布,而失真的 HSI 的光谱将偏离。给定一个原始的 $HSI \in R^{M \times N \times L}$,我们首先将局部归一化应用于光谱 $s$。
\[\bar s(\lambda) = \frac{s(\lambda) - \mu(\lambda)}{\sigma(\lambda) + C} \tag{1}\]其中 $\lambda = 1, 2, …, L$ 是光谱索引, $C$ 是用于当分母趋向于0时稳定规范化的常数。 实验中 $C$ 设置为 1。 $\mu(\lambda)$ 和 $\sigma(\lambda)$ 分别表示局部均值和标准差。
\[\mu(\lambda) = \sum_{k = -K}^K w_k s(\lambda + k) \tag{2}\] \[\sigma(\lambda) = \sqrt{\sum_{k = -K}^K w_k [s(\lambda + k) - \mu(\lambda)]^2} \tag{3}\]其中 $w = {w_k \mid -K, -K + 1, …, K}$ 是高斯权重窗口。 $K$ 决定窗口的宽度。局部归一化消除了局部均值位移,并使局部方差归一化,因此具有去相关性效果。局部归一化的光谱将比原始频谱更均匀。局部归一化后,原始 HSI 的光谱将大约具有零均值和单位方差。
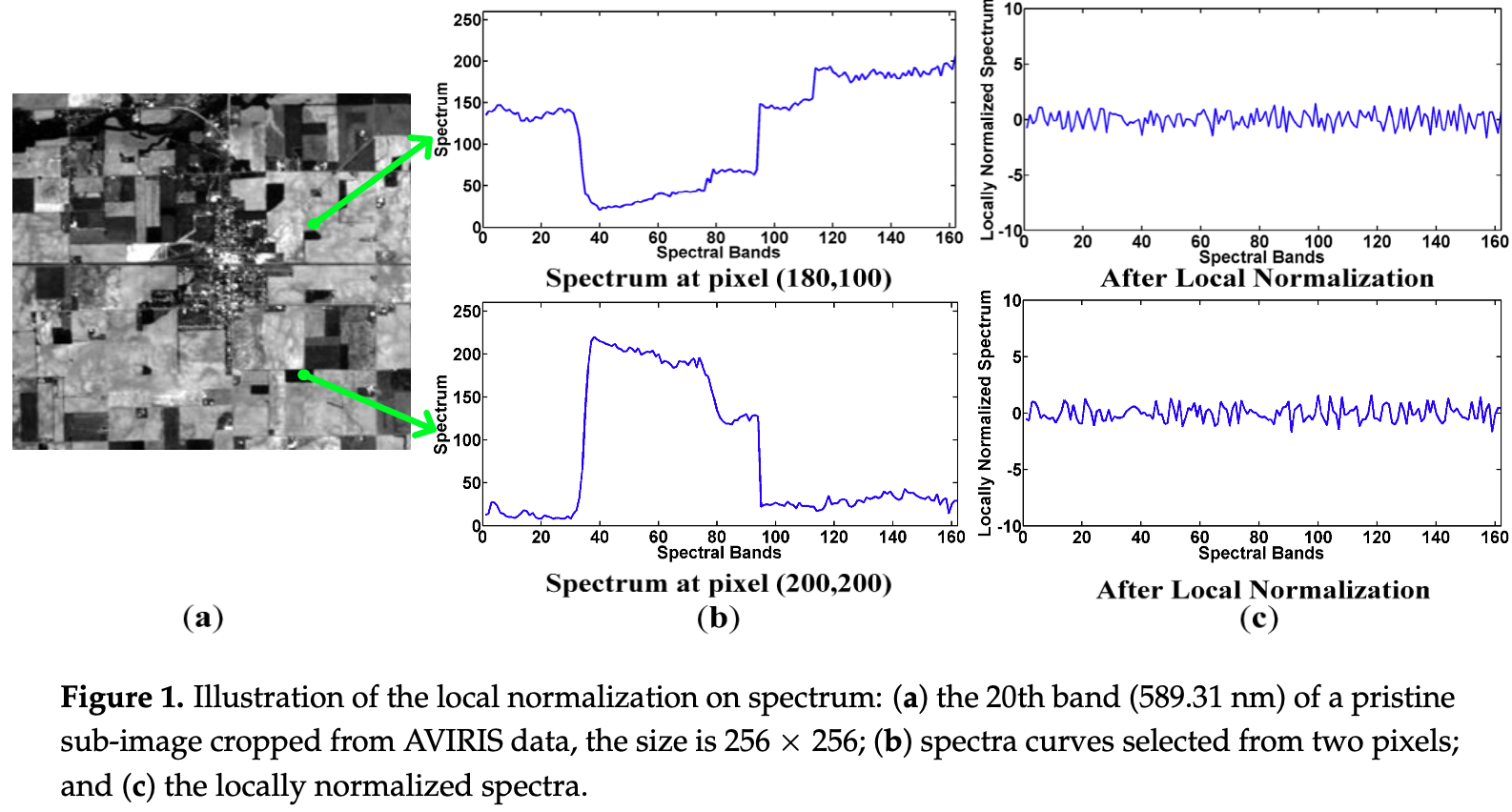
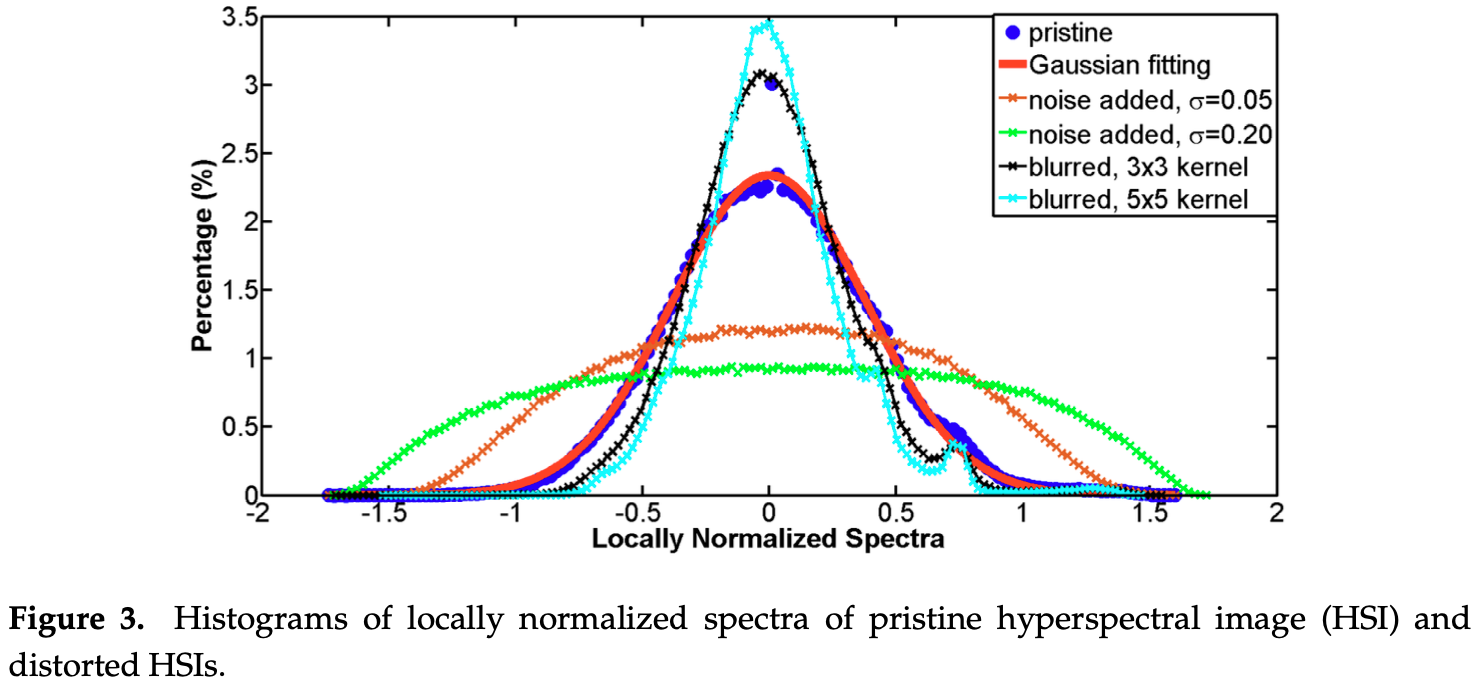
我们从AVIRIS数据[23]中裁剪一个子图像,然后将上述局部归一化应用于光谱,如图1所示。噪声和模糊是HSI[24-26]失真引起的常见影响,因此我们为原始HSI添加噪声或将其模糊以模拟失真HSI。图2显示了添加不同噪声级别(高斯噪声)和模糊(平均滤波)的子图像。我们绘制了图3中子图像中所有光谱的直方图。据观察,原始HSI的局部归一化光谱的分布遵循零均值的高斯分布,而失真的HSI的局部归一化光谱偏离。图3中有两个有趣的发现。首先,每种类型的失真都会以自己的方式修改分布。例如,随着噪声的增加,分布曲线变得平坦,并倾向于均匀分布。当HSI模糊时,分布曲线变得很薄,并倾向于拉普拉斯分布。其次,更严重的失真会导致分布的更大修改。标准差 $\sigma = 0.20$ 的噪声使分布曲线比 $\sigma = 0.05$ 的噪声平坦得多,$5 \times 5$ 模糊核产生比 $3 \times 3$ 核更窄的钟形曲线。

因此,光谱域中的一些统计属性可以通过失真来修改,测量这些统计数据的变化可以评估光谱失真。广义高斯分布(GGD)可用于捕获原始和失真的HSI之间的统计变化。零均值的GGD的函数是:
\[f(x; \alpha, \beta, \sigma^2) = \frac{\alpha}{2 \beta \Gamma(1 / \alpha)} \exp[-(\frac{\mid x \mid}{\beta})^{\alpha}] \tag{4}\]其中:
\[\beta = \sigma \sqrt{\frac{\Gamma(1 / \alpha)}{\Gamma (3 / \alpha)}} \tag{5}\] \[\Gamma(a) = \int_0^\infty t^{a-1} e^{-t} dt \qquad a > 0 \tag{6}\]其中 $\alpha$ 和 $\beta$ 分别表示形状参数和尺度参数。 $\sigma$ 是标准差。GGD 模型可以广泛描述多个分布的统计信息。当 $\alpha=1$ 和 $\alpha = 2$ 时, GGD模型简化为拉普拉斯分布和高斯分布。当 $\alpha$ 接近无穷大时,它倾向于均匀分布。当引入失真时,局部归一化光谱将偏离高斯分布,并倾向于均匀或拉普拉斯分布,所有这些都可以通过GGD模型捕获。GGD模型的统计信息由其模型参数描述,因此我们选择参数 [α,β] 作为光谱质量敏感特征,可以使用 moment-matching 算法[17]进行估计。
##