Deep Unfolding

病态逆问题通常求解下式：

\[y = \Phi x + n \tag{1}\]

从贝叶斯视角，可以使用最大后验估计（MAP），求解上式

\[\hat x = \text{arg} \max_x p(x \mid y) = \text{arg} \max_x \frac{p(y \mid x) p(x)}{p(y)} = \text{arg} \max_x p(y \mid x)p(x) \tag{2}\]

假设 $y$ 的加性高斯白噪声 $\epsilon \thicksim N(0, \sigma^2)$, MAP形式的等式（2）可以写作：

\[\begin{aligned} \hat x &= \text{arg} \max_x \exp[-\frac{1}{2 \sigma_\epsilon^2} \|y - \Phi x\|_2^2 + \log p(x)] \\ &= \text{arg} \min_x \frac{1}{2} \|y - \Phi x\|_2^2 - \sigma^2 \log p(x) \end{aligned}\tag{3}\]

通过将位置噪声变量 $\sigma_\epsilon^2$ 替换为噪声平衡系数 $\lambda$，将负对数先验函数 $p(x)$ 替换为正则项 $R(x)$，等式（3）可写作：

\[\hat x = \text{arg}\max_x \frac{1}{2} \| y - \Phi x\|_2^2 + \lambda R(x) \tag{4}\]

Proximal Gradient Descent (PGD)

PGD 算法通过以下迭代函数将等式（4）估计为迭代收敛问题：

\[\hat x^k = \text{arg} \min_x \frac{1}{2 \rho} \| x - (\hat x^{k-1} - \rho \Phi^T(\Phi \hat x^{k-1} - y))\|_2^2 + \lambda R(x) \tag{5}\]

它得到一个数据子问题（梯度下降）和一个先验子问题（近端映射）：

\[v^k = \hat x^{k-1} - \rho \Phi^T(\Phi x^{k-1} - y) \tag{6}\] \[\hat x^k = \text{prox}_{\lambda, J}(v^k) \tag{7}\]

HQS

为了解耦等式（3）中的数据项和先验项， HQS引入一个辅助变量 $z$，产生如下的优化问题：

\[\hat x = \text{arg} \min_x \frac{1}{2} \| y - \Phi x\| + \lambda R(z) \qquad s.t. \qquad z = x \tag{8}\]

上式可以通过最小化下列问题求解：

\[L_\mu(x, z) = \frac{1}{2} \|y - \Phi x\|^2 + \lambda R(z) + \frac{\mu}{2}\|z - x\|^2 \tag{9}\]

其中 $\mu$ 是惩罚参数。该问题可以通过迭代求解下列 $x$ 和 $z$ 子问题解决：

\[x_k = \text{arg} \min_x \|y - \Phi x\|^2 + \mu\|x - z_{k-1}\|^2 \tag{6a}\] \[z_k = \text{arg} \min_z \frac{1}{2(\sqrt{\lambda / \mu})^2} \| z - x_k \|^2 + R(z) \tag{6b}\]

(6a) 的子问题目标是找到一个 $z_{k-1}$ 的近端点，并且通常有一个快速地依赖于 $\Phi$ 的闭式解。 (6b) 的子问题从贝叶斯视角看，对应于在噪声等级为 $\sqrt{\lambda / \mu}$ 的 $x_k$ 上高斯去噪。

ADMM

ADMM 求解等式（3）可以写作：

\[x^{k+1} = \text{arg} \min_x \frac{1}{2}\|Ax - y\|_2^2 + \frac{\rho}{2}\|x - (z^k - \mu^k) \|_2^2 \tag{7}\] \[z^{k+1} = \text{arg}\min_z \lambda R(z) + \frac{\rho}{2}\| z - (x^{k+1} + \mu^k) \|_2^2 \tag{8}\] \[\mu^{k+1} = \mu^k + (x^{k+1} - z^{k+1}) \tag{9}\]

Eq. (9) 有闭式解：

\[x^{k+1} = (A^\top A + \rho I)^{-1} · [A^\top y + \rho(z^k - \mu^k)] \tag{10}\]

$AA^\top$ 是一个对角矩阵， $(A^\top A + \rho I)^{-1}$ 可以通过矩阵逆公式高效求解：

\[(A^\top A + \rho I)^{-1} = \rho^{-1} I - \rho^{-1} A^\top (I + \rho A A^\top)^{-1} A \rho^{-1} \tag{11}\]

Eq. (8) 可以重写为：

\[z^{k+1} = \text{arg} \min_z \frac{1}{2 (\sqrt{\lambda / \rho})^2} \| z - (x^{k+1} +\mu^k) \|_2^2 + R(z) \tag{12}\]

将 Eq. (12) 代入 Eq. (11) 得到：

\[x^{k+1} = (z^k - \mu^k) + A^\top [y - A(z^k - u^k)] ./ [\text{Diag}(AA^\top) + \rho] \tag{13}\]

其可以视为在噪声等级为$\sigma^2 = \lambda / \rho$ 的图像 $(x^{k+1} + \mu^k)$ 上高斯去噪：

\[z^{k+1} = \mathcal{D}_{\sigma_k}(x^{k+1}+\mu^k, \sqrt{\lambda / \mu}) \tag{14}\]

Diffusion Model

DDPM

前向过程：

\[q(x_{1:T} \mid x_0) := \prod_{t=1}^T q(x_t \mid x_{t-1}), \qquad q(x_t \mid x_{t-1}) := N(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t I) \tag{1}\]

前向过程任意时间步采样 $x_t$ 在有闭式解：令 $\alpha_t := 1 - \beta_t$, $\bar \alpha_t = \prod_{s=1}^t \alpha_s$，有：

\[q(x_t \mid x_0) = N(x_t; \sqrt{\bar \alpha_t}x_0, (1 - \bar \alpha_t)I)\]

SMLD

SDEs

ODEs

CASSI System

CASSI系统的退化可以归因于各种因素，包括编码模板、色散棱镜和CCD。编码模板表示为 $M \in R^{H \times W}$，作为原始信号 $X \in R^{H \times W \times N_\lambda}$ 的调制器，因此调制图像第 $n_\lambda^{th}$ 个波长表示为：

\[X'_{n_\lambda} = M \odot X_{n_\lambda}\]

然后，调制后的 HSI $X’$ 经过色散过程，其可以表示为：

\[X''(h, w, n_\lambda) = X'(h, w+d_{n_\lambda}, n_\lambda)\]

其中 $X’’ \in R^{H \times (W + d_{N_\lambda}) \times N_\lambda}$， $d_{n_\lambda}$ 表示第 $n_\lambda^{th}$ 个波长的位移距离。最后，位移后的编码高光谱图像被CCD捕获为2D观测图像。该过程可以公式化为：

\[Y = \sum_{n_\lambda = 1}^{N_\lambda} X''_{n_\lambda}\]

考虑观测噪声，向量形式的上式可以公式化为：

\[y = \Phi x + n\]

其中 $y \in R^{H \times W}, x \in R^{HWN_{\lambda}}$, $\Phi \in R^{HW \times HWN_{\lambda}}$。$\Phi$ 是一个块对角矩阵。

Note：每一行表示对每一个像素编码，一共有 $N_\lambda$ 个块，$N_\lambda$ 对应编码 $N_\lambda$ 个波段，因此是一个块对角矩阵, 如下图。

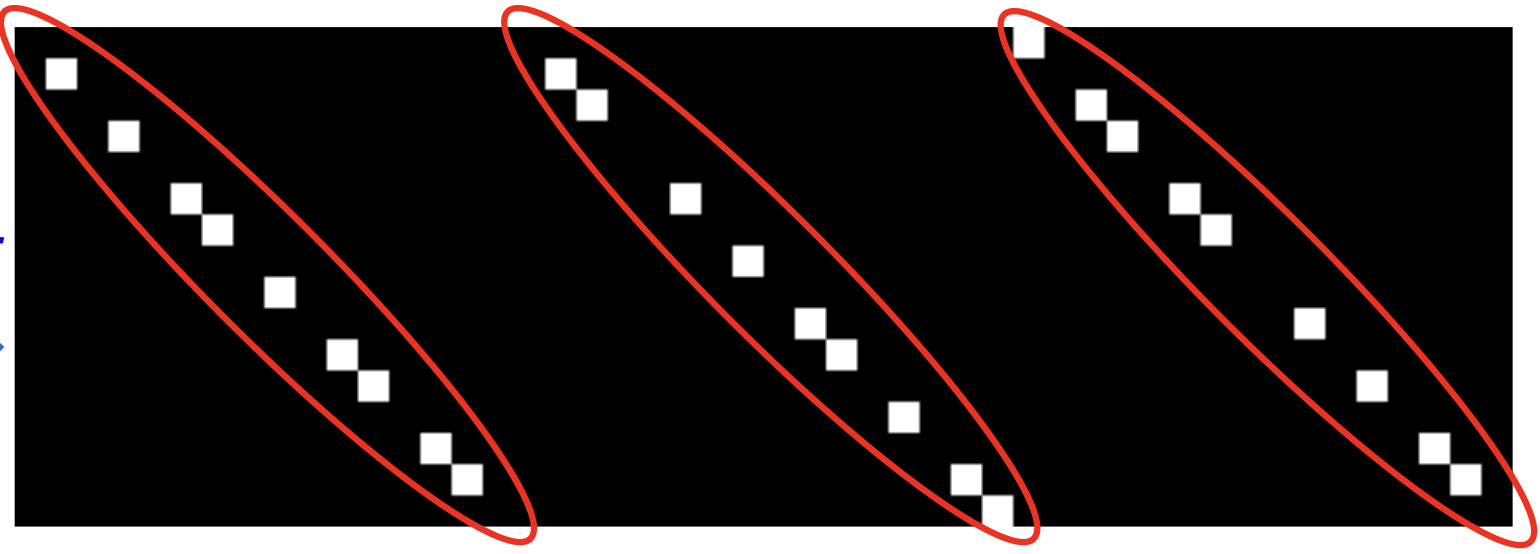
每个对角线模式对应于向量化的编码模板，相邻的对角线模式具有均匀的位移。 $\Phi \Phi^T$ 是一个对角矩阵，其相当于

Reference

Dong Y, Gao D, Qiu T, et al. Residual Degradation Learning Unfolding Framework with Mixing Priors across Spectral and Spatial for Compressive Spectral Imaging[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2023: 22262-22271.
Zhang K, Li Y, Zuo W, et al. Plug-and-play image restoration with deep denoiser prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 44(10): 6360-6376.
Zheng S, Liu Y, Meng Z, et al. Deep plug-and-play priors for spectral snapshot compressive imaging[J]. Photonics Research, 2021, 9(2): B18-B29.
Wang L, Sun C, Zhang M, et al. Dnu: Deep non-local unrolling for computational spectral imaging[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020: 1661-1671.

【深度学习】Deep Unfolding， Diffusion Model and CASSI