Abstract
在编码孔径快照光谱成像(CASSI)系统中,可以从捕获的压缩图像重构出真实世界的高光谱图像。
基于模型的HSI重构方法采用手工构建的先验来解决重构问题,但由于手工构建的先验表示能力较差,大多数方法的成功程度有限。
基于深度学习的方法直接学习压缩图像和 HSI 之间的映射,取得了更好的效果。
然而,为了获得满意的结果,设计一个强大的深度网络启发式算法是非常重要的。
这篇文章提出了一种新的基于最大后验(MAP)估计框架的HSI重建方法,使用学习到的高斯尺度混合(GSM)先验。
不同于现有的 GSM 模型使用手工制作的比例先验(例如,Jeffrey’s 先验),这篇文章通过深度卷积神经网络(DCNN)学习 scale 先验。
此外,这篇文章还提出利用DCNN 来估计 GSM 模型的 local means。
MAP 估计算法的所有参数和DCNN 参数通过端到端训练进行联合优化。
Introduction
与传统的RGB图像相比,高光谱图像(HSIs)具有更多的光谱波段,能够更准确地描述图像场景中的物质特征。基于其丰富的光谱信息,HSI 有助于许多计算机视觉任务,如:,目标识别,检测,跟踪。传统的成像系统使用 1D 和 2D 传感器需要很长的时间扫描场景, 不能捕获动态目标。最近,许多编码孔径快照光谱成像(CASSI)系统被提出以视频速率捕获3D HSI。CASSI利用 Physical mask 和 disperser 调制不同波长的信号,并将所有调制信号混合生成单个2D压缩 measurement 。然后采用重建算法从二维压缩图像重建出三维HSI。如图1所示,从真实 CASSI 系统捕获的二维压缩图像( measurement )重构了28个光谱波段。
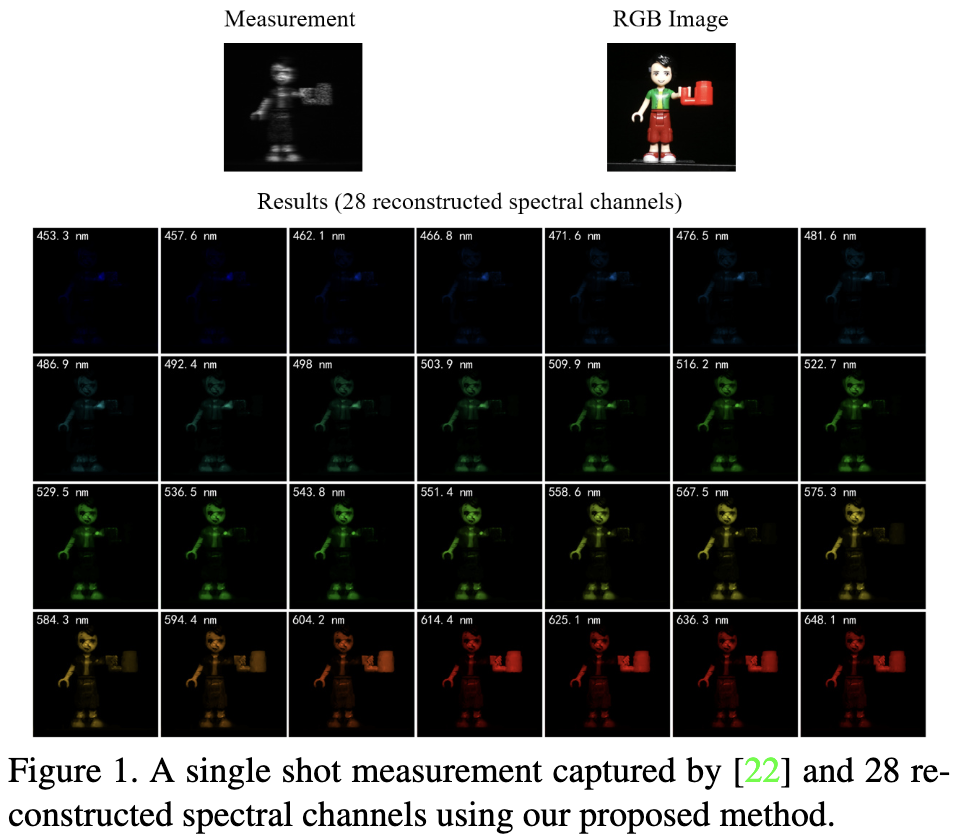
因此,重构算法在CASSI中起着举足轻重的作用。为了解决这一病态逆问题,以往的基于模型的方法采用手工制作先验对重构过程进行正则化。在GAP-TV中,引入 total variation 先验来解决 HSI 重构问题。基于 HSI 对某些字典具有稀疏表示的假设,基于稀疏性方法利用 $l_1$ 稀疏性对解进行正则化。考虑到 HSI 的像素具有强的长程依赖, 基于非局部的方法被提出。然而,基于模型的方法需要手工调整参数,导致重建速度慢,重建质量有限。受深度卷积神经网络(deep convolutional neural networks, DCNNs)用于自然图像恢复成功的启发,基于深度学习的 HSI 重建方法也被提出。在[36]中,将迭代HSI重建算法展开为DCNN,其中两个子网络利用空间-光谱先验。在 [37] 中加入了非局部自相似先验来进一步改进结果。除了受优化启发的方法外,还提出了基于 DCNN 的方法,该方法直接学习了2D measurement 和 3D HSI 之间的映射函数。λ-net 通过两阶段 DCNN 从二维measurement 数据和 mask 输入重建 HSI。TSA-Net[22]集成三个空间光谱自我注意模块到U-Net骨干[31]中,并取得了最先进的结果。虽然已经取得了良好的HSI重建性能,但设计一个强大的启发式DCNN并非易事。
考虑到上述问题,这篇文章提出了一种基于学习到高斯尺度混合(GSM)先验的可解释HSI重建方法。这篇文章的贡献如下:
- 提出利用学习到的GSM模型发掘 HSIs 的空间-光谱相关性。与现有的GSM模型使用手工制作的尺度先验不同(例如,Jeffrey’s 先验),这篇文章提出通过 DCNN 学习尺度先验。
- GSM模型的局部均值估计为空间-光谱相邻像素的加权平均值。利用 DCNN 估计空间-光谱相似度权重。
- HSI重建问题被表述为学习GSM模型的最大后验(MAP)估计问题。MAP estimator 中的所有参数以端到端方式进行联合优化。
- 在合成数据集和真实数据集上的大量实验结果表明,提出的方法优于现有的最先进的 HSI 重建方法。
The Proposed Method
GSM models for CASSI
将 HSI 重构公式化为最大后验估计(MAP)问题。 给定观测到的 measurement $y$, 要重构的 3D HSI $x$ 可以通过最大化后验估计:
\[\log p(x \mid y) \propto \log(y \mid x) + \log p(x)\]似然项可以用高斯函数建模:
\(p(y \mid x) = \frac{1}{\sqrt{2 \pi} \sigma} \exp (- \frac{\|y - Ax\|_2^2}{2\sigma^2})\) 对于先验项 $p(x)$, 提出将 HSI 的每个像素 $x_i$ 特征化为一个 标准差为 $\theta_i$ 的 nonzero-mean 的高斯分布。 有了 scale 先验 $p(\theta_i)$ 和 假设 $\theta_i$ 和 $x_i$ 相互独立, 我们可以使用如下的 GSM 模型建模 $x$:
\(p(x) = \prod_i p(x_i), \qquad p(x_i) = \int_0^\infty p(x_i \mid \theta_i) p(\theta_i) d\theta_i\) 其中 $p(x_i \mid \theta_i)$ 是一个均值为 $\mu_i$ 方差为 $\theta_i^2$ 的非零均值高斯分布:
\(p(x_i \mid \theta_i) = \frac{1}{\sqrt{2\pi}\theta_i} \exp(-\frac{(x_i - \mu_i)^2}{2\theta_i^2})\) 有了不同的 scale 先验, GSM 模型可以很好地表达很多分布。
对于 scale 先验 $p(\theta_i)$, 想比于用确定先验建模 $p(\theta_i)$, 这篇文章引入一种通用形式:
\[p(\theta_i) \propto \exp(-J(\theta_i))\]其中 $J(\theta_i)$ 是能量函数。 相比于计算 $p(x_i)$ 的解析表达式,这通常是 intracable 的, 作者提出通过替换 MAP 估计中的 $p(x)$ 为 $p(x, \theta)$ 来联合估计 $x$ 和 $\theta$。
Conclusion
这篇文章提出了一种编码孔径快照光谱成像的可解释高光谱图像重建方法。
与现有的研究不同,该网络是基于高斯尺度的混合先验。
利用GSM模型对高光谱图像进行特征提取,并将重建问题归结为MAP估计问题。
相比于人工设计先验, 提出一种从 DCNN 学习 GSM scale 先验。
此外,在自回归模型的启发下,GSM 模型的均值被估计为空间-光谱相邻像素的加权平均值,这些 filter coefficients 也被DCNN 估计,旨在学习充分的空间-光谱相关性的 HSI。
在合成数据集和真实数据集上的大量实验结果表明,该方法优于现有的先进算法。
这篇文章提出的网络不仅限于光谱压缩成像如CASSI和类似系统,它还可以用于视频快照压缩成像系统。
Summary
似然项用高斯函数建模, 先验项用高斯尺度混合模型建模。
HSI 重建可以看作一个最大后验估计 (MAP) 问题:
\[\log p(x \mid y) \propto \log p(y \mid x) + \log p(x) \tag{1}\]其中 $p(y \mid x)$ 是似然项, $p(x)$ 是先验分布。 似然项可以用高斯函数建模:
\[p(y \mid x) = \frac{1}{\sqrt{2 \pi} \sigma} \exp(- \frac{\|y - Ax\|_2^2}{2 \sigma^2}) \tag{2}\]先验项 $p(x)$ 用 标准差 $\theta_i$ 非零均值的高斯分布建模 HSI 的每个像素 $x_i$。
假设 $\theta_i$ 和 $x_i$ 相互独立, 可以用以下 GSM 模型建模 $x$:
\[p(x) = \prod_i p(x_i), \quad p(x_i) = \int_0^\infty p(x_i \mid \theta_i) p(\theta_i) d \theta_i \tag{3}\]其中 $p(x_i \mid \theta_i)$ 是方差为 $\theta_i^2$ 均值为 $u_i$ 的非零均值高斯分布:
\(p(x_i \mid \theta_i) = \frac{1}{\sqrt{2 \pi} \theta_i} \exp(- \frac{(x - u_i)^2}{2 \theta_i^2}) \tag{4}\) 有了不同的尺度先验, GSM 模型可以表示很多分布。
尺度先验 $p(\theta_i)$ , 相比于用具体先验建模 $p(\theta_i)$ , 引入一种通用形式:
\[p(\theta_i) \propto \exp(-J(\theta_i)) \tag{5}\]$p(x_i)$ 的解析表达式无法得到, 通过用 $p(x, \theta)$ 替换 MAP 中的 $p(x)$ 联合估计 $x$ 和 $\theta$:
\[\begin{align} (x, \theta) &= \mathop{\text{argmax}}_{x, \theta} \log p(y \mid x) + \log p(x, \theta) \\ &= \mathop{\text{argmax}}_{x, \theta} \log p(y \mid x) + \log p(x \mid \theta) + \log p(\theta) \end{align} \tag{6}\]通过将等式$(7)$ 中的高斯似然项 和先验项中的 $p(x_i \mid \theta_i)$ 和 $p(\theta_i)$ 代入上面的 MAP estimator, 得到以下目标函数:
\(\begin{align} (x, \theta) &= \mathop{\text{argmin}}_{x, \theta} \| y - Ax\|_2^2 + \sigma^2 \sum_{i=1}^N \frac{1}{\theta_i^2} (x_i - u_i)^2 + 2 \sigma^2 \sum_{i=1}^{N} \log \theta_i + 2 \sigma^2 J(\theta) \\ &= \mathop{\text{argmin}}_{x, \theta} \| y - Ax\|_2^2 + \sigma^2 \sum_{i=1}^N \frac{1}{\theta^2_i}(x_i - u_i)^2 + R(\theta) \end{align} \tag{7}\) ?
其中 $R(\theta) = 2 \sigma^2 \sum_{i=1}^N \log \theta_i + 2 \sigma^2 J(\theta)$。 因此 HSI 重构问题可以通过交替优化 $x$ 和 $\theta$ 求解。
对于 $x$ - subproblem , 固定 $\theta$, 我们可以通过求解下式求解 $x$:
\[x = \mathop{\text{argmin}}_x \| y - Ax \|_2^2 + \sum_{i=1}^N w_i(x_i - u_i)^2 \tag{8}\]其中 $w_i = \frac{\sigma^2}{\theta_i^2}$ , 均值 $u_i$ 与 $x$ 一起更新。 计算局部 spatial-spectral 邻近像素的加权平均作为均值 $u_i$ 的估计。
\[u_i = k_i^\top x_i \tag{9}\]为了求解等式 $(8)$, 我们可以应用梯度下降:
\[x^{(t+1)} = x^{(t)} - 2 \delta \{A^\top (A x^{(t)} - y) + w^{(t)}(x^{(t)} - u^{(t)})\} \tag{10}\]其中 $\delta$ 是步长。
对于 $\theta$- subproblem 可以改变为估计 $w$, 固定 $x$, $w$ 可以由以下等式估计:
\[w = \mathop{\text{argmin}}_w \sum_{i=1}^N w_i(x_i - u_i)^2 + R(w) \tag{11}\]$w$的解依赖于 $R(w)$ 的选择。对于一些先验, 可以得到 closed-form 解; 对于其他情况, 可以使用迭代算法。 但它们各有利弊。这里可以使用 DCNN 从 $x^{(t+1)}$ 估计 $w^{(t+1)}$ 。
-
Previous
【深度学习】CST:Coarse-to-Fine Sparse Transformer for Hyperspectral Image Reconstruction -
Next
【深度学习】PnP-DIP-HSI:Self-supervised Neural Networks for Spectral Snapshot Compressive Imaging