论文部分
理解原文的很多公式定理需要对测度论、 拓扑学等数学知识有所掌握,这里公式的部分我们只看结论就好。
作者首先讨论了各种loss函数的缺点,然后抛出了自己的loss函数。
KL散度(相对熵)
当为离散的随机变量时:
\[D_{KL}(p||q) = \sum_{i=1}^{n}p(x_i)log(\frac{p(x_i)}{q(x_i)})\]当为连续的随机变量时:
\[D_{KL}(P_r||P_g) = \int P_r(x) log(\frac{P_r(x)}{P_g(x)})d\mu(x)\]在机器学习中, P往往用来表示样本的真实分布, Q用来表示模型所预测的分布,那么KL散度可以计算计算两个分布的差异, 也就是Loss损失值。
如果$q(x_i)$大于$p(x_i)$, 那么$log(\frac{p(x_i)}{q(x_i)})$为负
如果$q(x_i)$小于$p(x_i)$, 那么$log(\frac{p(x_i)}{q(x_i)})$为正
如果$q(x_i)$等于$p(x_i)$, 那么$log(\frac{p(x_i)}{q(x_i)})$为0
然后用$p(x_i)$给$log(\frac{p(x_i)}{q(x_i)})$加权,求出$log(\frac{p(x_i)}{q(x_i)})$的期望
也就是说高概率的$p(x_i)$匹配区域比低概率的$p(x_i)$匹配区域更加重要。
因此$D_{KL}$的取值范围为0到inf。
有时会将KL散度称为KL距离,但它并不满足距离的性质:
- KL 散度是非对称,即 $D(p|q)$ 不一定等于 $D(q|p)$
- KL散度不满足三角不等式
JS散度
JS散度度量两个概率分布的相似度,基于KL散度的变体,解决了KL散度非对称的问题。
一般,JS散度是对称的, 其取值是0到1之间,定义如下:
\[JS(P_1\|P_2) = \frac{1}{2}KL(P_1\|\frac{P_1+P_2)}{2}) + \frac{1}{2}KL(P_2\|\frac{P_1 + P_2}{2})\]Wasserstein距离[EM距离(Earth Mover (EM) distance)]
它的定义非常直观:假设有两堆数据分布P和Q,看作两堆土,现在把P这堆土推成Q这堆土所需要的最少的距离就是EM距离
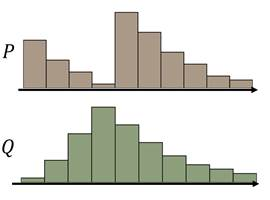
假设P的分布是上图棕色柱块区域,Q的分布是上图绿色柱块区域,现在需要把P的分布推成Q的分布,我们可以制定出很多不同的MovingPlan(推土计划)
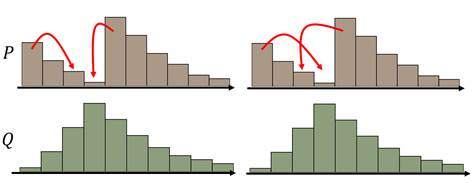
这些不同的推土计划都能把分布P变成分布Q,但是它们所要走的平均推土距离是不一样的,我们最终选取最小的平均推土距离值作为EM距离。例如上面这个例子的EM距离就是下面这个推土方案对应的值。
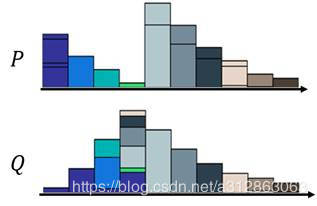
那为了更好地表示这个推土问题,我们可以把每一个moving plan转化为一个矩阵图:
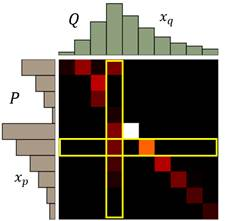
每一个色块表示P分布到Q分布需要分配的土量(移动距离),那每一行的色块之和就是P分布该行位置的柱高度,每一列的色块之和就是Q分布该列位置的柱高度。于是我们的求解目标表达式就如下所示:

表达式中$\gamma$函数计算当前计划下$x_P$到$x_Q$的推土量, $|x_P - x_Q|$表示二者之间的推土距离
那如果这个时候我们想直接求解这个表达式的话,是非常麻烦的,因为需要穷举所有的moving plan然后再选择其最小值。如果我们对之前的理论有印象的话,我们会想到这个optimization problem依然可以交给discriminator来解决。
于是接下来要做的,就是去改discriminator,让它能够衡量与之间的wasserstein距离
KL散度和JS散度存在的问题:
如果两个分布P、Q离得很远,完全没有重叠的时候,KL散度是没有意义的, 而JS散度值是一个常数。意味着这一点梯度为0, 梯度消失了。
Wasserstein距离
Wasserstein距离度量两个概率分布之间的距离, 定义如下:
\[W(P_1, P_2) = \inf_{\gamma \thicksim \Pi (P_1, P_2) }E_{(x, y)\thicksim \gamma}[\|x - y\|]\]$\Pi (P_1, P_2)$是$P_1$和$P_2$分布组合起来的所有可能的联合分布的集合。
对于每一个可能的联合分布$\gamma$, 可以从采样$(x, y)\thicksim \gamma$得到一个样本x和y, 并计算出这对样本的距离$|x-y|$, 所以可以计算该联合分布$\gamma$下,样本对距离的期望值$E(x, y) \thicksim \gamma[|x - y|]$, 即样本的均值等于分布的期望。
在所有的联合分布中能够对这个期望值取到的下界$infy \thicksim \Pi(P_1, P_2)E(x,y) \thicksim \gamma[|x-y|]$就是Wasserstein距离。
直观上可以把$E(x,y)∼γ[|x−y|]$理解为在$γ$这个路径规划下把土堆P1挪到土堆P2所需要的消耗。而Wasserstein距离就是在最优路径规划下的最小消耗。所以Wesserstein距离又叫Earth-Mover距离。
Wasserstein距离相比KL散度、JS散度的优越性在于,即便两个分布没有重叠,Wasserstein距离仍然能够反映它们的远近;而JS散度在此情况下是常量,KL散度可能无意义。WGAN本作通过简单的例子展示了这一点。考虑如下二维空间中的两个分布$P_1$和$P_2$,$P_1$在线段AB上均匀分布,$P_2$在线段CD上均匀分布,通过控制参数$\theta$可以控制着两个分布的距离远近。
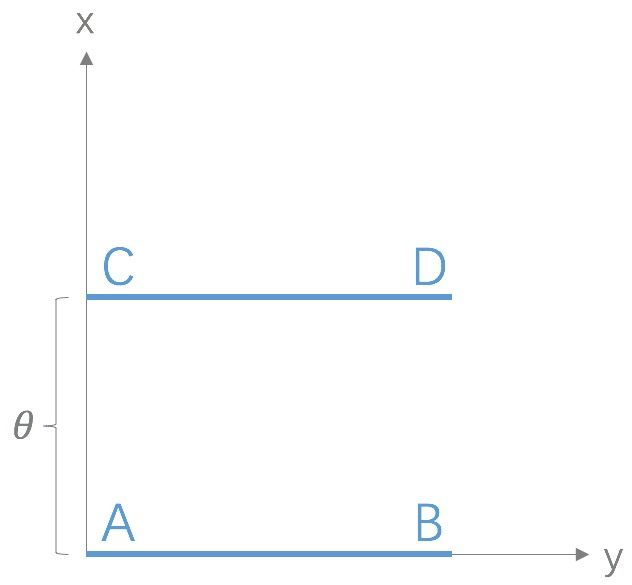
此时得到:
\[KL(P_1||P_2) = KL(P_1||P_2) = \begin{cases}+\infty & {if \theta \neq 0} \\ 0 & {if \theta = 0} \end{cases} (突变)\] \[JS(P_1||P_2) = \begin{cases}log2 & {if \theta \neq 0} \\ 0 & {if \theta = 0} \end{cases}(突变)\] \[W(P_0, P_1) = |\theta|(平滑)\]KL散度和JS散度是突变的,要么最大要么最小, Wasserstein距离却是平滑的,如果我们要用梯度下降法优化$\theta$这个参数,前两者根本提供不了梯度,Wasserstein距离却可以。类似地,在高维空间中如果两个分布不重叠或者重叠部分可忽略,则KL和JS既反映不了远近,也提供不了梯度,但是Wasserstein却可以提供有意义的梯度。
WGAN的损失函数
生成器的损失函数
原始GAN生成器的损失函数为:
\[E_{x\thicksim P_g}[log(1-D(x))]\]通过变换,可以用JS散度表示为:
\[2JS(P_r||P_g)- 2log2\]如果$P_r$与$P_g$之间重叠部分接近与0, 那么其JS散度就是常数$log2$, 其梯度为0, 无法使用梯度下降法进行学习。
并且,Pg与Pr之间的重叠部分为0的概率非常大【注解1】。此外,随着D判别Pg与Pr的能力增强,重叠部分将越来越小
因此,原始GAN的不稳定表现为:如果D训练得太好,G的loss趋近于常数,梯度为0,无法进行梯度下降;另一方面,如果D训练得不好,G的梯度不稳,难以向Pr收敛【注解2】
在原始GAN后, WGAN前,Ian Goodfellow对G的损失函数进行了改进:
\[E_{x\thicksim P_g}(-log(D(x)))\]-logD(x)函数却存“自相矛盾”与“惩罚偏好”两个问题【注解3】,导致GAN训练不稳定,并且容易出现模式崩溃。
【注解1】 Pg与Pr之间的重叠部分为0的概率较大
原因是:生成器G将低维噪声Pz映射为高维样本Pg(比如从100维映射为784维),784维的Pg的各种变化已经被100维的Pz限定死了,也就是Pg实际上是在784维空间定义了一个100维的数据分布(学术层面上来讲就是,生成样本的分布Pg实际上是高维空间中的低维流形)。然而另一方面,Pr本身就是高维的,也就是在784维空间定义了一个784维的数据分布。类比到三维空间,Pg是二维的面或者一维的线,而Pr充满三维空间,Pg与Pr之间的重叠部分就只会是一个面或者一条线,在三维空间中相当于“0” (高维空间中的低维流形与高维流形之间的重叠几乎为“0”)。
因此,如果D接近最优,判别能力较强,也就是能够完全将Pg与Pr分开,那么Pg与Pr之间的JS散度就接近常数,求导为0。
【注解2】如果D训练得不好,G的梯度不稳,难以向Pr收敛
Pz从低维空间映射到高维空间的映射方式有无数种,映射结果又无数种可能性,如果D的判别能力较弱,G就可能不受约束,向着不满足要求的方向映射。
\[E_{x\thicksim P_g}(-log(D(x)))\]-logD(x)函数的“自相矛盾”与“惩罚偏好”问题
生成器损失函数为:
\[KL(P_g\|P_r) - 2JS(P_r\|P_g)\]该函数可以变换为:
通过该公式可以看出损失函数具有以下两个问题:
(1)自相矛盾:
最小化改损失函数的时候就相当于最小化KL距离,同时最大化JS散度,自相矛盾。
\[P_g(x)log\frac{P_g(x)}{P_r(x)} \rightarrow 0\](2)惩罚偏好:
当$P_g \rightarrow 0, P_r \rightarrow 1$,即$P_g$的多样性远低于$P_r$, 对KL距离贡献为0,惩罚微小;
\[P_g(x)log\frac{P_g(x)}{P_r(x)}\rightarrow + \infty\]当$P_g \rightarrow 1, P_r \rightarrow 0$, 即$P_g$的多样性远高于$P_r$, 对KL距离的贡献为无穷, 惩罚巨大;
基于此, G更倾向于舍弃多样性,而生成“重复且安全”样本,带来模式崩溃问题。
判决器的损失函数
原始GAN判决器的损失函数
\[\min_D\max_G V(G, D) = E_{x\thicksim P_{data}}(log(D(x)))+E_{x\thicksim P_G}(log(1 - D(G(x))))\]然后引入了WGAN(Wasserstein-GAN), 使用了EM距离。
WGAN的Discriminator的目标表达式:
\[V(G, D)= \max_{D\in1-Lipschitz}{E_{x\thicksim P_{data}}[D(x)] - E_{x\thicksim P_G}[D(x)]}\]这个式子的意思也就是feed给Discriminator真实数据(即x来自于data的分布)得到的输出 减去 Generator生成 feed给Discriminator的假数据(即x来自于G的分布)的输出,最后再加上一个1-Lipschitz约束。
既然Discriminator想要最大化这个值,那么$E_{x\thicksim P_{data}}[D(x)]$就会越来越大,$E_{x\thicksim P_G}[D(x)]$ 就会越来越小。
1-Lipschitz约束:
\[\|f(x_1) - f(x_2)\| \leq K\|x_1 - x_2\|\]其中K=1 for “1-Lipschitz”
为什么要给Discriminator做限制?
传统GANs的discriminator输出的结果是在(0,1)区间之内,但是在WGAN中输出的结果是was距离,was距离是没有上下界的,这意味着,随着训练进行,$P_G$的was值会越来越小,$P_{data}$的was值会越来越大,discriminator将永远无法收敛。
在最原始的WGAN中,采用的做法是weight clipping,很简单,设定一个上限c与下限-c,如果更新参数w大于c,改成w=c;如果更新参数w小于-c,改成w=-c。这样D在$P_G$与$P_{data}$处的值就不会被无限拉远。但是这个方法并没有让D真的限制在1-Lipschitz function内,所以原始的WGAN并没有严格地给出was距离计算方法
直到后来,直到WGAN的增强版WGAN-GP,以及SNGAN被提出,才解决了这个问题。
Lipschitz continuity
利普希茨连续。满足如下性质的任意连续函数 f 称为 K-Lipschitz:
\[|f(x_1) - f(x_2)| \leq K|x_1 - x_2|, \forall x_1, x_2 \in domf\]直观上看,Lipschitz 条件限制了函数变化的剧烈程度。
Weight clipping
在利用 gradient descent 进行参数更新后,在对所有参数进行如下操作:
\[w = \begin{cases}c, & \text{if w>c} \\ -c, & \text{if w<-c}\\w & \text{otherwise} \end{cases}\]其中 c 是人为设定的阈值。注意,Weight cplipping 并无法保证 f 位于 1-Lipschitz,而只能保证其是 K-Lipschitz的(K具体无法确定)
WGAN相较于DCGAN的改动
- 判决器最后一层去掉sigmoid
- 生成器和判决器的loss不取log
- 每次更新判决器的参数之后把它们的绝对值截断到不超过一个固定常数c
- 不要用基于动量的优化算法(包括momentum和Adam), 推荐RMSProp, SGD也行
精彩,如此复杂的理论,展现出来却这么漂亮。
实现部分

关于backward
backward()函数的第一个参数,在PyTorch的文档上解释的比较晦涩。该参数名为gradient,我理解这个参数在我上述的模型上表示
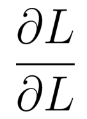
也就是element全为1的Tensor。为何这样设计,这样设计的意图可以理解为当我们不知道L关于y的函数表示,但知道L关于y的梯度时,我们可以通过 y.backward(-1 * torch.ones(2, 2, dtype=torch.float)) 来完成BP过程。注意,y.backward()的第一个参数,即是L关于y的梯度的值
通常情况下对于L为标量的情况,使用L.backward()时,不指定任何参数,PyTorch会使用维度相协调的全1Tensor作为参数。对于L为高于1维的情况,需要明确指定backward()的第一个参数。
backward(* grad_output)[source]
定义了operation的微分公式。 所有的Function子类都应该重写这个方法。 所有的参数都是Tensor。他必须接收和forward的输出 相同个数的参数。而且它需要返回和forward的输入参数相同个数的Tensor。 即:backward的输入参数是 此operation的输出的值的梯度。backward的返回值是此operation输入值的梯度
引入相关包
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import argparse
import os
import numpy as np
import math
import sys
import torchvision.transforms as transforms
from torchvision.utils import save_image
from torch.utils.data import DataLoader
from torchvision import datasets
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch
输入参数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
parser = argparse.ArgumentParser()
parser.add_argument("--n_epochs", type=int, default=200, help="number of epochs of training")
parser.add_argument("--batch_size", type=int, default=64, help="size of the batches")
parser.add_argument("--lr", type=float, default=0.00005, help="learning rate")
parser.add_argument("--n_cpu", type=int, default=8, help="number of cpu threads to use during batch generation")
parser.add_argument("--latent_dim", type=int, default=100, help="dimensionality of the latent space")
parser.add_argument("--img_size", type=int, default=64, help="size of each image dimension")
parser.add_argument("--channels", type=int, default=3, help="number of image channels")
parser.add_argument("--n_critic", type=int, default=5, help="number of training steps for discriminator per iter")
parser.add_argument("--clip_value", type=float, default=0.01, help="lower and upper clip value for disc. weights")
parser.add_argument("--sample_interval", type=int, default=400, help="interval betwen image samples")
opt = parser.parse_known_args()[0]
print(opt)
img_shape = (opt.channels, opt.img_size, opt.img_size)
cuda = True if torch.cuda.is_available() else False
当在jupyter下使用parser.parse_args()出错 则改换为parser.parse_known_args()[0]
生成器
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
self.init_size = opt.img_size // 4
# 第一层是为了把的噪声(batch_size, 100)
# 拉到 (batch_size, 128, img_size, img_size)
self.l1 = nn.Sequential(nn.Linear(opt.latent_dim, 128 * self.init_size ** 2))
self.conv_blocks = nn.Sequential(
nn.BatchNorm2d(128),
nn.Upsample(scale_factor=2),
nn.Conv2d(128, 128, 3, stride=1, padding=1),
nn.BatchNorm2d(128, 0.8),
nn.LeakyReLU(0.2, inplace=True),
nn.Upsample(scale_factor=2),
nn.Conv2d(128, 64, 3, stride=1, padding=1),
nn.BatchNorm2d(64, 0.8),
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(64, opt.channels, 3, stride=1, padding=1),
nn.Tanh(),
)
def forward(self, z):
out = self.l1(z)
out = out.view(out.shape[0], 128, self.init_size, self.init_size)
img = self.conv_blocks(out)
return img
判决器
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
def discriminator_block(in_filters, out_filters, bn=True):
block = [nn.Conv2d(in_filters, out_filters, 3, 2, 1), nn.LeakyReLU(0.2, inplace=True), nn.Dropout2d(0.25)]
if bn:
block.append(nn.BatchNorm2d(out_filters, 0.8))
return block
self.model = nn.Sequential(
*discriminator_block(opt.channels, 16, bn=False),
*discriminator_block(16, 32),
*discriminator_block(32, 64),
*discriminator_block(64, 128),
)
# The height and width of downsampled image
ds_size = opt.img_size // 2 ** 4
# 这里相较于DCGAN删去了sigmoid函数
self.adv_layer = nn.Sequential(nn.Linear(128 * ds_size ** 2, 1))
def forward(self, img):
out = self.model(img)
out = out.view(out.shape[0], -1)
validity = self.adv_layer(out)
return validity
参数初始化及优化器
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 这里相较于DCGAN没有使用交叉熵
# Initialize generator and discriminator
generator = Generator()
discriminator = Discriminator()
if cuda:
generator.cuda()
discriminator.cuda()
# Initialize weights
generator.apply(weights_init_normal)
discriminator.apply(weights_init_normal)
# Configure data loader
dataloader = torch.utils.data.DataLoader(
datasets.ImageFolder(
"data/",
transform=transforms.Compose(
[transforms.Resize(opt.img_size), transforms.ToTensor(), transforms.Normalize([0.5], [0.5])]
),
),
batch_size=opt.batch_size,
shuffle=True,
)
# Optimizers
# 这里相较于DCGAN,Adam优化器换成了RMSprop
optimizer_G = torch.optim.RMSprop(generator.parameters(), lr=opt.lr)
optimizer_D = torch.optim.RMSprop(discriminator.parameters(), lr=opt.lr)
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor
训练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
# ----------
# Training
# ----------
for epoch in range(opt.n_epochs):
for i, (imgs, _) in enumerate(dataloader):
# Configure input
real_imgs = Variable(imgs.type(Tensor))
real_imgs = real_imgs.resize_(imgs.shape[0], opt.channels, opt.img_size, opt.img_size)
# ---------------------
# Train Discriminator
# ---------------------
# Sample noise as generator input
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
# Generate a batch of images
gen_imgs = generator(z)
optimizer_D.zero_grad()
# Measure discriminator's ability to classify real from generated samples
real_loss = discriminator(real_imgs)
fake_loss = discriminator(gen_imgs.detach())
# was距离是要最大化 real_loss - fake_loss
# 这里加上一个符号,loss下降就相当于最大化was距离
d_loss = torch.mean(-real_loss + fake_loss)
d_loss.backward()
optimizer_D.step()
# Clip weights of discriminator
for p in discriminator.parameters():
p.data.clamp_(-opt.clip_value, opt.clip_value)
# Train the generator every n_critic iterations
if i % opt.n_critic == 0:
# -----------------
# Train Generator
# -----------------
optimizer_G.zero_grad()
# Sample noise as generator input
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
# Generate a batch of images
gen_imgs = generator(z)
# Loss measures generator's ability to fool the discriminator
g_loss = torch.mean(-discriminator(gen_imgs))
g_loss.backward()
optimizer_G.step()
print(
"[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]"
% (epoch, opt.n_epochs, i, len(dataloader), d_loss.item(), g_loss.item())
)
batches_done = epoch * len(dataloader) + i
if batches_done % opt.sample_interval == 0:
save_image(gen_imgs.data[:25], "images/%d.png" % batches_done, nrow=5, normalize=True)
实验结果
总结
WGAN将判决器sigmoid函数取消,损失函数不用交叉熵,将判决器从分类任务变成了一个回归任务。
这个回归任务就是穷举所有的moving plan然后再选择其最小值。

事实上,笔者在用celeba数据集训练WGAN时,遇到了各种问题,其中一个问题是D_loss很小,G_loss不断上升。 经过调整clip_value,学习率有改善。
但是效果还是不如直接用DCGAN。
这个问题在知乎有个回答
wgan与普通gan训练相比有什么需要注意的地方?为何dcgan改为wgan–gp 后反而不收敛?
理想的w距离应该是开始迅速增大,然后达到一个拐点,缓慢下降。
WGAN和WGAN-GP其实并不会收敛到纳什均衡。这个问题在规模的mnist上好不会太明显,但在大数据集大模型上体现就很明显了。但是这并不是完全否认WGAN,学界认为WGAN效果很好,WGAN即便没有收敛到纳什均衡,也会在纳什均衡点附近,因此依然是一个很好的方法,只是需要改良一下。
Reference
- Arjovsky M, Chintala S, Bottou L. Wasserstein gan[J]. arXiv preprint arXiv:1701.07875, 2017.
- 令人拍案叫绝的Wasserstein GAN
- 【学习笔记】生成模型——生成对抗网络
- PyTorch的学习笔记02 - backward( )函数
- PyTorch-GAN-master中的wgan的理解
- fastai/courses/dl2/wgan.ipynb
- PyTorch-GAN/implementations/wgan/wgan.py
- DL中常用的三种K-Lipschitz技术
- GAN ZOO 第2节: 对原始GAN的损失函数进行改进:LSGAN、WGAN、WGAN-GP
- wgan与普通gan训练相比有什么需要注意的地方?为何dcgan改为wgan–gp 后反而不收敛?