代数系统
等幂律
设*是定义在集合A上的一个二元运算, 如果对于任意的$x \in A$, 都有$x * x = x$, 则称运算*是等幂的。
同构
如果双射函数h是从代数A到A’的同构, 那么:
- 两个代数必须有相同的构成成分
- 在函数h的作用下, A的每一运算保持
- 函数映射A的每一常数到A’的对应常数
例子:
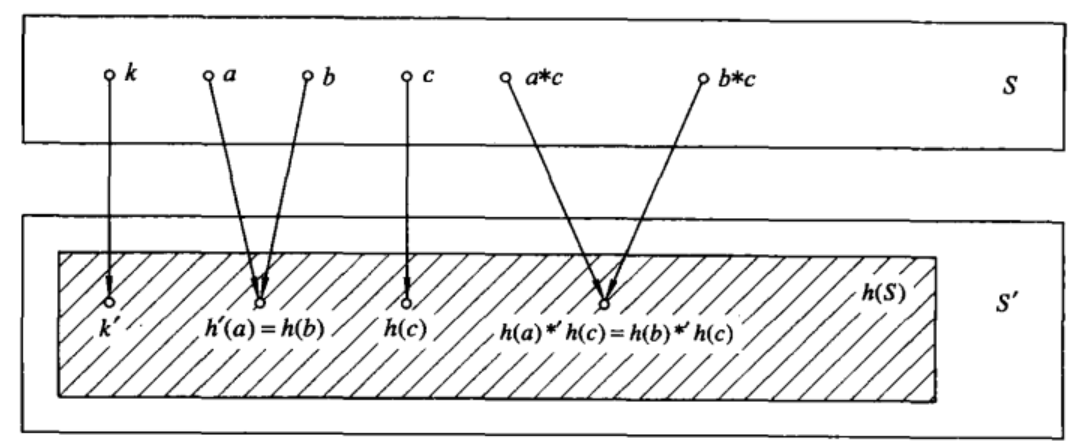
代数$A = (S, *, \triangle, k)$和$A’ = (S’, *’, \triangle’, k’)$是同构的,如果存在一双射函数h,使:
- $h: S \rightarrow S’$
- $h(a * b) = h(a) *’ h(b)$
- $h(\triangle a) = \triangle’ h(a)$
- $h(k) = k’$
这里a、b时S的任意元素。 映射h叫做A到A’的同构, A’叫做A在映射h下的同构象。
同态
放弃同构定义中, $h: S \rightarrow S’$必须是双射函数的要求, 但仍保持其它条件, 这就得到数学上的同态的概念。
例子:
代数$A = (S, *, \triangle, k)$和$A’ = (S’, *’, \triangle’, k’)$是同构的,如果存在一函数h,使:
- $h: S \rightarrow S’$
- $h(a * b) = h(a) *’ h(b)$
- $h(\triangle a) = \triangle’ h(a)$
- $h(k) = k’$
这里a、b是S的任意元素, 则称h是从A到A’的同态, $(h(S), *’, \triangle ‘, k’)$称为A在映射h下的同态象
半群
设$V = <S, o>$是代数系统, o为二元运算, 如果o运算是封闭的、可结合的, 则称V为半群。
独异点
若$e \in S$是关于o运算的单位元, 则称V是含幺半群, 也叫做独异点。独异点V记作 $V = <S, o, e>$。
口语描述:半群有么元就是独异点。
群
- 封闭性
- 结合律
- 有么元
- 每个元素有逆元
口语描述:独异点加上逆元就是群
子群
问题: 一个群在什么条件下有非平凡子群,为什么?
平凡群:只包含单一元素e的群
平凡子群:对任何群G都存在子群。 G和{e}都是G的子群, 称为G的平凡子群。
设$<G, *>$是一个群, S是G的非空子集, 如果$<S, *>$也构成群, 则称$<S, *>$是$<G, *>$的一个子群。
有限群和无限群
设$<G, *>$是一个群。 如果G是有限集, 那么称$<G, *>$为有限群
G中的元素的个数通常称为该有限群的阶数, 记为$\mid G\mid$
如果G是无限集, 则称$<G, *>$为无限群
交换群(阿贝尔群)
群中的二元运算是可交换的
陪集和拉格朗日定理
左陪集(右陪集)
设$<H, *>$是群$<G, *>$的一个子群, $a \in G$, 则集合\(\{a\}H(H\{a\})\)称为由a所确定的H在G中的左陪集(右陪集), 简称为H关于a的左陪集(右陪集), 记为\(aH(Ha)\)。元素a称为陪集aH(Ha)的代表元素。
拉格朗日定理
Klein四元群
设\(G = \{e, a, b, c, d\}\), o为G上的二元运算, 它由运算表9-6给出,不难证明G是一个群, 由表中可以看出G的运算具有下面的特点:
- e为G中的么元
- o是可交换的
- 任何G中的元素与子集运算的结果都等于e
- 在a, b, c三个元素中, 任何两个元素运算的结果都等于另一个元素
一般称这个群为Klein四元群
循环群
设$<G, *>$为群, 若在G中存在一个元素a, 使得G中任意元素都由a的幂组成, 则称该群为循环群, 元素a为循环群的生成元。
证明: 证明四阶群g必为循环群或klein群
证明 由拉格郎日定理可知,四阶群的元素的阶一定能整除群的阶4,故四阶群的元素的阶只能是1(幺元是唯一的1阶元),2,4,如果有一个元是4阶元,则该元自乘能生成群的所有元素,此时它是循环群,这个4阶元素是该循环群的生成元,否则如果除幺元外,所有的元均是2阶元,则此时该群正是4阶klein群.
群同态
前面在证明一个映射是否为同构映射的时候,都是先证明映射是一个双射,再证明它是否为同构映射。一个映射为双射是它为同构映射的必要条件。一般来说,条件越多,满足所有条件的可能性就越小,所以人们往往会推而广之,减少条件,使某个概念满足更加普遍的情况(就像矩阵的逆和它的左逆,右逆)。对于同构来说,就有一个更加一般性的概念 — 同态。同态并不要求映射是一个双射,只需要是个满射即可。直观的说,同态映射的像会比原来的群要“小”一些
设 (G,+),(H,∗) 是群,那么 G 到 H 的映射 f 称为 G 到 H 的同态映射。 对任意的 a,b∈G ,都有
\[f(a + b) = f(a) * f(b)\]格与布尔代数
格
设$<A, \leq>$是一个偏序集, 如果A中任意两个元素都有最小上界和最大下界, 则称$<A, \leq>$为格。
格诱导的代数系统
设$<A, \leq>$是一个格,如果在A上定义两个二元运算$\lor$和$\land$, 使得对于任意的$a, b \in A$
子格
设$<A, \leq>$是一个格, 由$<A, \leq>$诱导的代数系统为$<A, \lor, \land>$, 设$B \subseteq A$且$B \neq \emptyset$, 如果A中的这两个运算关于B是封闭的, 则称$<B, \leq>$为$<A, \leq>$的子格。
分配格
设$<A, \lor, \land>$是由格$<A, \leq>$所诱导的代数系统。 对任意的$a, b, c \in A$, 满足$a \land (b \lor c) = (a \land b) \lor (a \land c)$和$a \lor (b \land c) = (a \lor b) \land (a \lor c)$, 则称$<A, \leq>$是分配格。
设L是格, 则L是分配格当且仅当L不含有与钻石格或五角格同构的子格。
有界格
一个格中如果有一个元素比其他元素都大,这个元素叫做全上界, 记作1. 一个格中如果有一个元素比其他元素都小, 这个元素叫做全下界, 记作0.
有全下界和全上界的格叫做有界格
有补格
设$<L, \land, \lor, 0, 1>$是有界格, $a \in L$, 若存在$b \in L$使得$a \land b = 0$和$a \lor b = 1$成立, 则称b是a的补元
从图中来看, 是两个元素有共同的上确界和下确界。
设$<L. \land, \lor, 0, 1>$是有界格, 若L中所有元素都有补元存在, 则称L为有补格。
有补格加上分配格, 补元唯一。
布尔格(布尔代数)
如果一个格是有补分配格, 则成它为布尔格或布尔代数。
环与域
环
设$<A, \bigstar, *>$是一个代数系统, 如果满足:
- $<A, \bigstar>$是阿贝尔群
- $<A, *>$是半群
- 运算$*$对运算$\bigstar$是可分配的
则称$<A, \bigstar, *>$是环
域
设$<F, +, *>$是一个代数系统,如果满足:
- $<F, +,*>$是环
- \(<F - \{0\}, *>\)是交换群
则称$<A, +, ·>$是域。
图论
完全图:任意两个顶点之间都有边
补图: n个顶点的完全图减去该图, 就是该图的补图。
欧拉图
欧拉回路:图G的一个回路,如果恰通过图G的每一条边,则该回路称为欧拉回路,具有欧拉回路的图称为欧拉图。欧拉图就是从图上的一点出发,经过所有边且只能经过一次,最终回到起点的路径。
欧拉通路:即可以不回到起点,但是必须经过每一条边,且只能一次。也叫”一笔画”问题
基图:基图是针对有向图的说法,是忽略有向图的方向得到的无向图。
欧拉图:存在欧拉回路的图。
欧拉图是指通过图(无向图或有向图)中所有边且每边仅通过一次通路,相应的回路称为欧拉回路。
口语描述:看能不能一笔画。
定理1: 无向图G为欧拉图,当且仅当G为连通图且所有顶点的度为偶数。
推论1: 无向图G为半欧拉图,当且仅当G为连通图且除了两个顶点的度为奇数之外, 其它所有顶点的度为偶数。
哈密尔顿图
哈密尔顿路径: 穿程于G的每个结点一次且仅一次的路径称为哈密尔顿路径。
哈密尔顿回路: 穿程于G的每个结点一次且仅一次的回路称为哈密尔顿回路。
哈密尔顿图: 具有哈密尔顿回路的图为哈密尔顿图。
平面图
一个无向图$G = <V, E>$, 如果能把它图示在一平面上, 边与边只在顶点处相交, 则该图为平面图。
欧拉公式
任何一个凸多面体的顶点数n, 棱数m和面数k满足公式:
\[n - m + k = 2\]