条件概率
在B事件发生的情况下,A事件发生的概率$P(A \mid B)$
假设一个实验有N个等可能的结果,事件A和事件B分别包含$M_1$和$M_2$个结果, 这其中有$M_{12}$个结果是公共的, 如图所示:
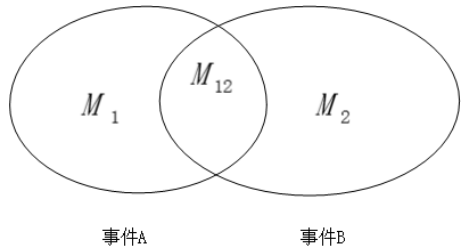
不难得出,B发生的前提下,A发生的概率为:$P(A \mid B) = \frac{M_{12}}{M_2}$
条件概率的表达式分析:
\[P(A \mid B) = \frac{M_{12} / N}{M_2 / N} = \frac{P(AB)}{P(B)}\]事件的独立性
\[P(A) = P(A \mid B)\]则事件A和事件B相互独立, 此时B事件发生的概率不为0。
PS: 这里不严谨, 比如“已知向上的点数是偶数, 那么向上点数大于4”的概率是多少?
设向上的点数是偶数为事件B, 向上的点数大于4为事件A, 那么:
\[P(A \mid B) = \frac{1}{3}\] \[P(A) = \frac{1}{3}\]此时$P(A \mid B) = P(A)$, 显然A、B是不独立的
\[P(A \mid B) = \frac{P(AB)}{P(B)} \Rightarrow P(AB) = P(A \mid B)P(B) = P(A)P(B)\]即
\[A、B相互独立 \Leftrightarrow P(AB) = P(A)P(B)\]全概率公式
若$B_1, B_2, …, B_n$两两互斥, 且它们之和为事件的全集, 即:
\[B_i B_j = \phi \\ B_1 + B_2 + ... + B_n = \Omega\]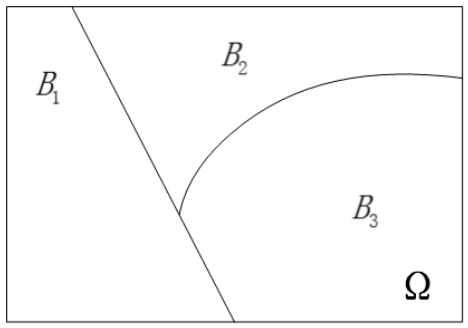
我们引入事件A
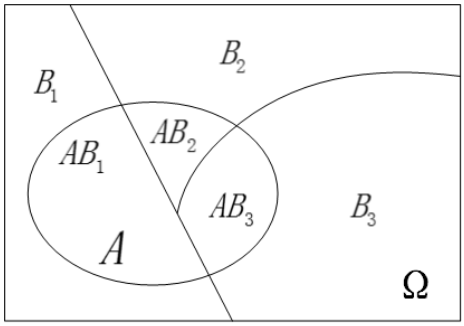
因此,有:
\[P(A) = P(A \Omega) = P(AB_1 + AB_2 + AB_3 + ... + AB_n)\]$B_i$、$B_j$两两互斥, $AB_1$、 $AB_2$、…、 $AB_n$两两互斥,因此:
\[P(A) = P(AB_1) + P(AB_2) + ... + P(AB_n)\]由条件概率公式$P(AB_i) = P(B_i)P(A \mid B_i)$,将上式转化:
\[P(A) = P(B_1)P(A \mid B_1) + P(B_2)P(A \mid B_2) + ... + P(B_n)P(A \mid B_n)\]这就是 全概率公式
$P(A)$就是各$P(A \mid B_k)$以$P(B_k)$为权的加权平均值
贝叶斯公式
由条件概率公式和全概率公式:
\[P(B_i \mid A) = \frac{P(AB_i)}{P(A)} = \frac{P(B_i)P(A \mid B_i)}{P(A)} \\ = \frac{P(B_i)P(A \mid B_i)}{P(B_1)P(A \mid B_1) + P(B_2)P(A \mid B_2) + ... + P(B_n)P(A \mid B_n)}\]这就是贝叶斯公式
本质内涵:由因到果, 由果推因
\[P(A) = P(B_1)P(A \mid B_1) + P(B_2)P(A \mid B_2) + ... + P(B_n)P(A \mid B_n)\]全概率公式由各种原因推出结果事件发生的概率, 是由因到果
\[P(B_i \mid A) = \frac{P(AB_i)}{P(A)} = \frac{P(B_i)P(A \mid B_i)}{\sum_j P(B_j)P(A \mid B_j)}\]贝叶斯公式求得的是条件概率,观察到某种现象,反推这种现象的各种原因的概率, 是由果推因
先验概率和后验概率
单纯的概率$P(B_i)$叫做先验概率, 指的是在没有别的前提信息的情况下的概率, 一般需要借助我们的经验估计得到。
条件概率$P(B_i \mid A)$叫做后验概率, 代表获得了信息A之后$B_i$发生的概率, 后验概率是先验概率获取了新信息之后的一种修正。
贝叶斯公式的应用
贝叶斯公式应用的一个常见例子就是 光片的病理推断案例,在某个病人的 光片中,医生看 到了一个阴影,这就是结果事件A,我们希望对造成这个结果的三种可能原因(原因 1:恶性肿瘤;原因 2:良性肿瘤;原因 3:其他原因)进行分析判断,推断分属于各个原因的概率,如图所示:
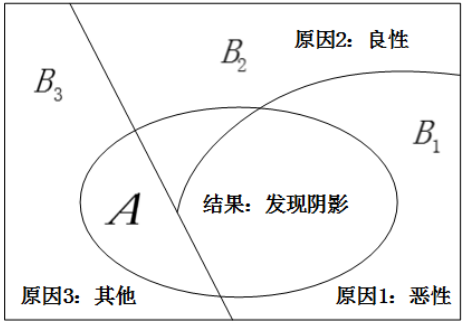
若想求出原因是恶性肿瘤的概率,也就是条件概率:$P(B_1 \mid A)$的值
我们需要知道三种原因下出现阴影的概率: $P(A \mid B_1)$, $P(A \mid B_2)$, $P(A \mid B_3)$
三种原因的先验概率: $P(B_1), P(B_2), P(B_3)$
通过贝叶斯公式可计算得到:
\[P(B_1 \mid A) = \frac{P(B_1)P(A \mid B_1)}{P(B_1)P(A \mid B_1) + P(B_2)P(A \mid B_2) + P(B_2)P(A \mid B_2)}\]