事件与随机变量
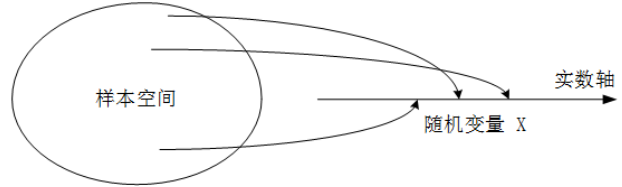
定义:某一次具体试验中所有可能出现的结果构成一个样本空间, 对于样本空间中的每一个可能的实验结果, 关联到一个特定的数。 这种实验结果与数的对应关系形成了随机变量
离散型随机变量
定义: 随机变量的取值只能是有限多个或者是可数的无限多个值。
随机变量关注的要素:
- 随机变量的取值
- 试验中每个对应取值的概率
- 随机变量的统计特征和度量方法
分布列和概率质量函数(probability mass function PMF)
随机变量 表示两次抛掷硬币正面向上的次数,随机变量 的分布列如下表所示:
| 取值 | 0 | 1 | 2 | 其他 |
|---|---|---|---|---|
| P | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{1}{4}$ | 0 |
概率质量函数就是将随机变量的每个值映射到其概率上,看上去和分布列就是一回事儿。
二项分布和二项随机变量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from scipy.stats import binom
import matplotlib.pyplot as plt
import seaborn
seaborn.set()
fig, ax = plt.subplots(3, 1)
params = [(10, 0.25), (10, 0.5), (10, 0.8)]
x = range(0, 11)
for i in range(len(params)):
binom_rv = binom(n=params[i][0], p=params[i][1])
ax[i].set_title('n={},p={}'.format(params[i][0], params[i][1]))
ax[i].plot(x, binom_rv.pmf(x), 'bo', ms=8)
ax[i].vlines(x, 0, binom_rv.pmf(x), colors='b', lw=3)
ax[i].set_xlim(0, 10)
ax[i].set_ylim(0, 0.35)
ax[i].set_xticks(x)
ax[i].set_yticks([0, 0.1, 0.2, 0.3])
plt.show()
QA
Q1: 本科我们接触概率密度函数多一些, 但概率质量函数接触地较少, 那你能解释一下概率质量函数和概率密度函数的区别吗?
Q2: 二项分布的概率值可以由参数为λ=np的泊松分布的概率值近似,当n和p的取值在哪个范围内,使得泊松分布近似值较为接近?