马尔科夫链的极限行为
极限与初始状态无关的情况
我们接着社会阶层流动概率转移矩阵来引入极限行为的话题。
对于转移概率矩阵
\[\begin{matrix} \left[\begin{array}{rr} 0.7 & 0.2 & 0.1 \\ 0.3 & 0.5 & 0.2 \\ 0.2 & 0.4 & 0.4 \end{array}\right] \end{matrix}\]随着转移步数$n$的逐步增大, $n$步转移概率矩阵收敛于
\[\begin{matrix} \left[\begin{array}{rr} 0.46808511 & 0.34042553 & 0.19148936 \\ 0.46808511 & 0.34042553 & 0.19148936 \\ 0.46808511 & 0.34042553 & 0.19148936 \\ \end{array}\right] \end{matrix}\]当$n \rightarrow \infty$时, 矩阵中每一个值都会收敛于一个极限值, 这个极限值不依赖于初始状态$i$。
换句话说, 过来很多代之后,处于任何一个阶层的概率都是一定的,跟祖先的状态已经没有关系了。
极限依赖与初始状态的情况
这是一个老虎和养的故事。
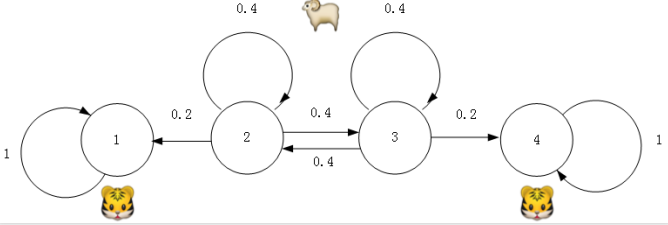
转移概率图如下:
\[\begin{matrix} \left[\begin{array}{rr} 1 & 0 & 0 & 0 \\ 0.2 & 0.4 & 0.4 & 0 \\ 0 & 0.4 & 0.4 & 0.2 \\ 0 & 0 & 0 & 1 \end{array}\right] \end{matrix}\]经过计算, 随着$n \rightarrow \infty$, $n$步转移概率矩阵收敛于:
\[\begin{matrix} \left[\begin{array}{rr} 1 & 0 & 0 & 0, \\ 0.6 & 0 & 0 & 0.4 \\ 0.4 & 0 & 0 & 0.6 \\ 0 & 0 & 0 & 1 \end{array}\right] \end{matrix}\]这个矩阵的内涵:
- 这四个状态中,有两个状态可以被称作“吸收”状态, 也就是说一旦到达了这个状态, 就不会再有任何机会转移到其他状态, 而是将永远处于这个状态。
- $n$步转移概率矩阵在数值上也会收敛, 但是收敛的极限值会依赖于初始状态。 最开始的杨如果位于区域2,它死于区域1的老虎的概率是0.6, 而如果杨最开始位于区域3, 则它死于区域1的老虎的概率时0.4。
- 随着$n \rightarrow \infty$, $n$步转移概率矩阵中, 状态2和状态3两列都收敛为0。 无论羊初始位于那个状态,只要时间够长,它们都会落入虎口, 没有活下来的希望。
可达、常返与常返类、
可达性
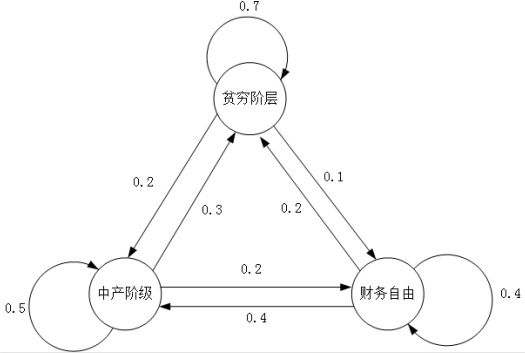
阶级流动概率转移图中,任意两个状态都可以互相到达。 而羊入虎口概率转移图如果从状态1出发,除了自身以外, 到达不了任何其他的状态。
常返
对于任意一个状态$i$, 如果对于每个从状态$i$出发可达的状态$j$, 相应地从状态$j$出发,反过来也可到达状态$i$, 那么状态$i$就是常返的。
用数学语言描述:
我们令状态$i$的可达集合为$A(i)$, 对于集合$A(i)$中的每一个状态$j$, 如果$i \in A(j)$, 那么状态$i$就是常返的。
常返类
如果状态$i$时一个常返状态, 那么状态$i$的可达状态集就是构成了一个常返类。
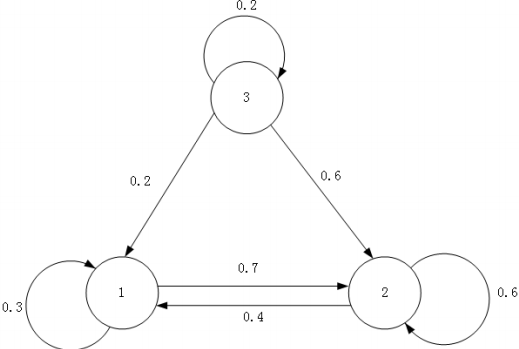
状态1和状态2是常返状态, 状态3是非常返状态, 同时状态1的可达状态集是{状态1, 状态2}, 因此状态1和状态2构成了一个常返类。
于是这个马尔科夫链就被分解成为了一个常返类和一个非常返状态。
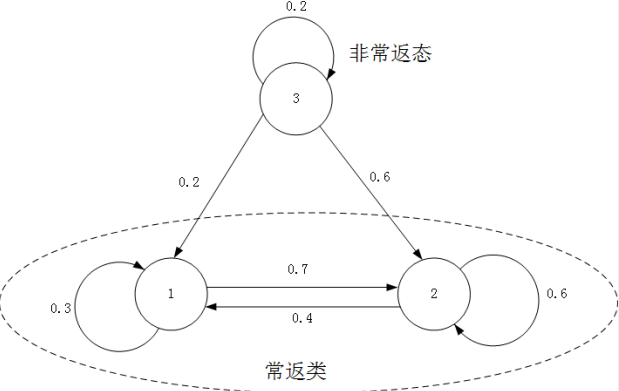
从图中,可以概括出一些直观且重要的结论:
第一就是常返类只进不出
第二就是不管开局如何, 终将进入常返类
对于有多个常返类的马尔科夫链, 一定不会收敛于一个唯一的稳态分布。
周期性问题
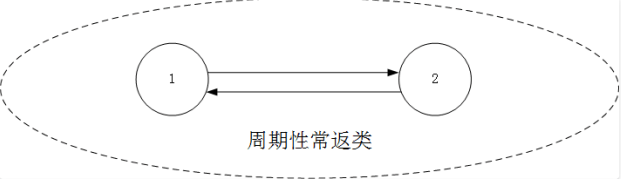
如果常返类是周期性的,如上图所示, 那么它从状态1出发,即使$n \rightarrow \infty$, 如果n为奇数, 则转移到状态2, 如果n为偶数, 则状态转移到状态1, 显然是不收敛的。
判断一个常返类$R$是不是周期的方法: 只要存在一个特定的$n \geq 1$, 和$R$中某一个特定的状态$i$, 使得经过$n$步之后可以到达常返类$R$中的任意状态, 那么这个常返类就是非周期的。
在上面的图中,不存在这样的n, 因此它是周期的。
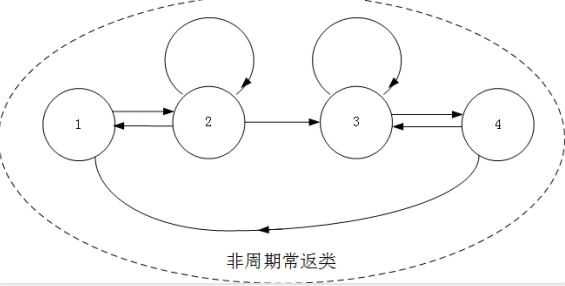
下面这幅图中, 当$n=3$时, 从状态1出发,可以到达常返类中的四个状态${1, 2, 3, 4}$, 因此它时非周期的。
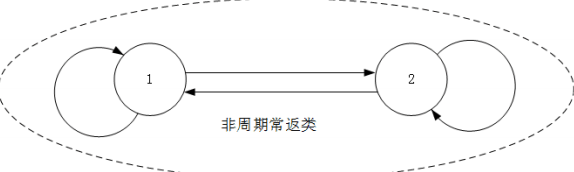
对于一开始那张图,做一点修改,就能改成非周期的。
马尔科夫链的稳态分析
稳态的定义
当$n \rightarrow \infty$时, n步转移概率矩阵中每个数值收敛。
对于马尔科夫链中的每一个状态$j$, $n$步转移概率值$r_{ij}(n)$会趋向于一个独立于初始状态$i$的极限值, 通常把这个极限值记作$\pi_j$。
独立于初始状态$i$, 意味着无论从哪个初始状态开始, 经过$n$步转移($n \rightarrow \infty$ )到状态j的概率都是$\pi_j$。 在稳态下, 处于状态$j$的概率也同样趋近于极限值$\pi_j$, 即$P(X_n = j) \rightarrow \pi_j$(当$n \rightarrow \infty$)。
当$n \rightarrow \infty$, 马尔科夫链要收敛于一个稳态分布, 首先它得是非周期的, 其次如果要求这个稳态分布时唯一的, 则这个马尔科夫链必须只含有一个常返类。
不可约条件
一个不可约的马尔科夫链指的是, 从任意一个状态出发, 当经过充分长时间之后, 可以到按任意状态, 否则就叫做可约的。
含有多个常返类的肯定是可约的, 即使只有一个常返类, 也不一定就是不可约的。
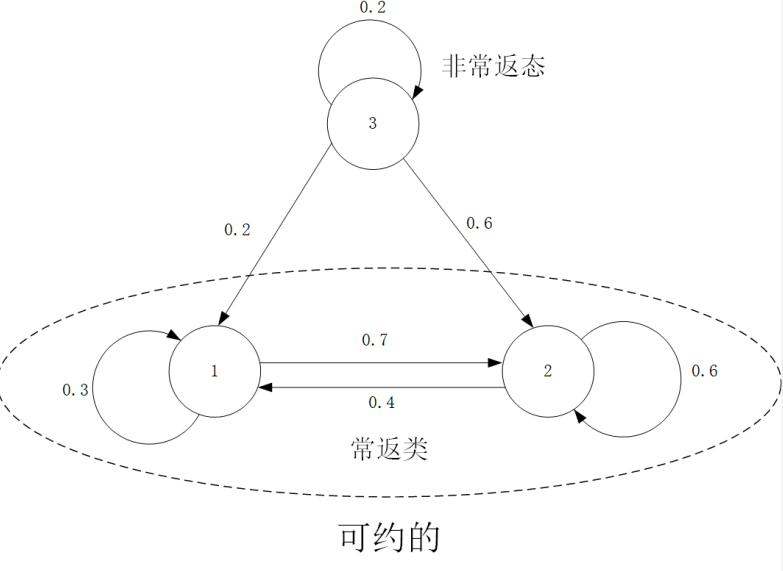
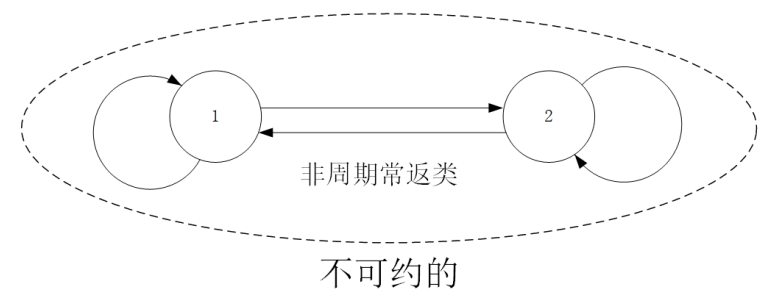
满足不可约条件意味着马尔科夫链的各个状态之间时全联通的, 这个条件是为了确保随着$n \rightarrow \infty$, 马尔科夫链收敛的唯一稳态分布中的每个状态的概率都大于0。
正常返
对于任意一个状态, 从其他任意一个状态出发,当时间趋于无穷时, 首次转移到这个状态的概率不为0。
怎么理解?
常返就是, a状态能到b状态, b状态也能到a状态。
正常返就是这个事件早晚都会发生的例如抛硬币,早晚会抛到正面!非常返就是不确定这个事件会不会发生例如图二(举例比较单一。还有很多情况)。
正常返是常返的一个子类, 表示在常返的概念基础上, 还附加一个转移步数有限的条件。
这个条件主要针对无限状态的马尔科夫链, 它也是为了保证在这种情况下,马尔科夫链收敛的唯一稳态分布中的每一个状态都大于0。
唯一平稳分布存在性的判定: 在不可约、非周期、正常返的条件下, 马尔科夫链拥有唯一稳态分布, 且每个状态的概率都大于0。
稳态的求法
我们还是对照阶级流动的马尔科夫链的状态转移图来观察。
QA
Q1: 能不能举一个是常返但不是正常返的例子