研究问题描述

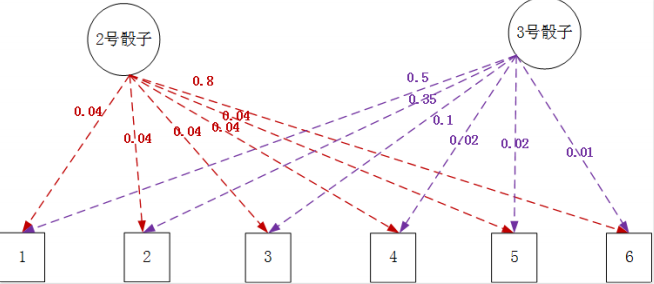
例子：老千手上有三个骰子， 1号骰子是正常的， 2号骰子和3号骰子都是特制的，他每次使用其中一个骰子进行投掷，并且不停地偷偷对这三个骰子进行切换使用。

我们不知道他使用地是哪个骰子，这对应地就是隐藏状态，而由骰子掷出的点数就是观测。

观测序列概率估计

当我们知道老千切换三个骰子的转移概率矩阵以及各个骰子输出各个点数的概率的基础上，我们可以计算出任意一个观测序列出现的概率。

用隐马尔科夫模型的形式化语言就是：在给定隐马尔可夫模型三要素$\lambda = (A, B, \pi)$, 针对一个具体的观测序列$O = (o_1, o_2, …, o_T)$，求它出现的概率。

马尔科夫模型三要素：

扔出⼀串指定点数骰⼦的概率，那么⽤条件概率来表⽰我们的计算⽬标就是：求$P(O \mid \lambda)$的概率。

对于同一个观测序列$O$而言，可以对应不同的隐含状态序列$I$，实际上所有的隐含状态序列$I$都能够以一定的概率生成这个观测序列$O$。

$P(O \mid \lambda)$的求解过程就可以看作是通过对一系列不同$I$和指定对应$O$的联合概率进行求和，最终的都边缘概率的过程：$P(O \mid \lambda) = \sum_I P(O, I \mid \lambda)$。

然后联合概率$P(O, I \mid \lambda)$按照贝叶斯公式展开有： $P(O, I \mid \lambda) = P(O \mid I, \lambda)P(I \mid \lambda)$，我们代入到原始公式中，目标式子转化成了：

\[P(O \mid \lambda) = \sum_I P(O \mid I, \lambda)P(I \mid \lambda)\]

对于任意一个隐含状态序列，我们设它的序列为： $I = (i_1, i_2, i_3, …, i_T)$，同时转移概率矩阵为A，那么生成这个隐含状态的概率：

\[P(I \mid \lambda) = \pi_{i_1}a_{i_1i_2}a_{i_2 i_3}...a_{i_{T-1}i_T}\]

$P(O \mid I, \lambda)$的本质就是利用这个已知的隐含状态序列$I = (i_1, i_2, i_3, …, i_T)$去生成指定的观测序列$O = (o_1, o_2, …, o_T)$，运用输出概率矩阵B：

\[P(O \mid I, \lambda) = b_{i_1o_1}b_{i_2o_2}...b_{i_To_T}\]

我们把它合并起来有：

\[P(O, I \mid \lambda) = P(O \mid I, \lambda)P(I \mid \lambda) = \pi_{i_1}b_{i_1o_1}a_{i_2i_3}b_{i_2i_3}...a_{i_{T-1}i_T}b_{i_To_T}\]

看上去$P(O, I \mid \lambda) = P(O \mid I, \lambda)P(I \mid \lambda)$的计算并不难，就是2T次乘法运算。

但是对于$P(O \mid \lambda) = \sum_I P(O, I \mid \lambda)$, 它的外面还有一个求和的$\sum$运算，相当于对每一个可能出现的隐含状态都要进行2T次乘法运算。

所有的隐含状态有多少个？序列长度为T，隐含状态集中有N个状态，那么所有的隐含状态序列的个数就是$N^T$，整个运算的时间复杂度就是$O(2TN^T)$，也就是$O(TN^T)$

当我们知道老千切换三个骰子状态转移概率和各个骰子输出各个点数的概率时，我们可以通过已经的观测序列，也就是骰子的点数序列，来解码出老千所使用骰子的序列，也就是隐状态序列。也就是可以推测出每一个掷出的点数背后，老千到底用的那一个骰子，可以判断他什么时候出千。

用隐马尔可夫模型的形式化语言概括就是：在给定隐马尔科夫模型三要素$\lambda = (A, B, \pi)$和观测序列$O = (o_1, o_2, …, o_T)$的基础上，求最有可能对应的隐藏状态序列$I = (i_1, i_2, …, i_T)$