向量
在⾃然语⾔处理中,程序在进⾏⽂本阅读时,⾸先就会进⾏⽂本分词,然后使⽤向量进⾏表⽰。这是因为向量很适合 在⾼维空间中进⾏表达和处理。在本书后续内容中将接触到的投影、降维等概念,都是在向量的基础上实现的。
将⼀个矩阵 A 所表⽰的线性映射作⽤于某向量 x 时,我们习惯于将其写成矩阵乘以向量的形式——Ax,而这种写法的 运算基础便是:x 是⼀个列向量。
向量的 Python 表⽰
NumPy 中的转置⽅法在⼀维向量⾥是⽆效的。
1
2
3
import numpy as np
A=np.array([1,2,3,4])
print(A.transpose())
## 向量的内积
向量与向量的乘法分为所谓的 点乘(内积) 和 叉乘(外积)
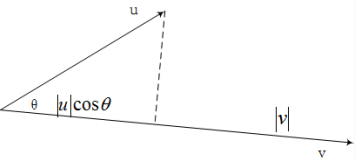
向量 u 和向量 v 的内积定义如下:
\[u \times v = [u_1 \quad u_2]^T · [v_1 \quad v_2]^T = u_1v_1 + u_2v_2\]它的另⼀种表⽰⽅法所含的物理意义就⼗分清晰:$u · v = \mid u \mid \mid v \mid cos \theta$, 如图所示:
NumPy 函数库中的内积⽅法 dot,那么 Python 内积运算函数 dot 中的参数要求必须是⼀维列向量:
1
2
3
4
import numpy as np
u=np.array([3,5,2])
v=np.array([1,4,7])
print(np.dot(u,v))
## 向量的外积
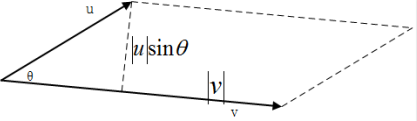
我们只讨论⼆维平⾯和三维空间中的向量外积,在⼆维平⾯中:
\[u \times v = [u_1 \quad u_2]^T \times [v_1 \quad v_2]^T = u_1v_2 - u_2v_1\]同样地,还有另⼀种表达式,看起来物理意义会更直观⼀些:$u \times v = \mid u \mid \mid v \mid sin \theta$, 如图所示, 表⽰两个向量张成的平 ⾏四边形的⾯积,当然,这⾥的⾯积要打引号,因为如果两个向量的夹⻆⼤于 180°,则结果为负。
1
2
3
4
import numpy as np
u=np.array([3,5])
v=np.array([1,4])
print(np.cross(u,v))
而在三维空间中,外积的计算要相对复杂⼀些,其计算的结果是⼀个向量而不是⼀个数值。
\[u\times v= \begin{bmatrix} u_1&u_2&u_3 \end{bmatrix} ^{T}\times \begin{bmatrix} v_1&v_2&v_3 \end{bmatrix} ^{T} = [u_2v_3 - u_3v_2 \quad u_3v_1 - u_1v_3 \quad u_1v_2 - u_2v_1]\]基底
向量的坐标取决于基底
对于向量$u = [4 \quad 5]^T$而⾔,我们⼀直以来都很理所应当的认为:它表⽰⼀条在 x 轴上投影为 4,y 轴上投影为 5 的有向线段,它的坐标是 (4,5)。这其实是基于了⼀个我们没有刻意强调的前提:我们是利⽤ 了⽅向为 x 轴、 y 轴正⽅向并且⻓度为 1 的两个向量 $e_x = [1 \quad 0]^T$、$e_y = [0 \quad 1]^T$作为讨论的基准。因此, 对向量u的完整写法就是$u = 4e_x + 5e_y, u = 4[1 \quad 0]^T + 5[0 \quad 1]^T$。
因此关于向量 u 的完整准确的说法是:在基底 ($e_x$, $e_y$)下,其坐标是$[4 \quad 5]^T$。也就是说,坐标必须依托于指定的基底才有意义。因此,要想准确地描述向量,⾸先要确定⼀组基,然后通过求 出向量在各个基向量上的投影值,最终才能确定在这个基上的坐标值。
同⼀向量在不同基底上表⽰为不同坐标
例如,我们可以选择不使⽤默认的基底$[1 \quad 0]^T$和$[0 \quad 1]^T$ ,而选择这两个看似普通的向量$[1 \quad 1]^T$和$[-1 \quad 1]^T$作为新的基。
根据向量内积的介绍,我们最好是把基向量的模⻓转化为 1,因为如果模是 1,那么就可以⽤⽬标向量点乘基向量,从而直接获得其在这个基向量上的对应坐标。实际上对应任何⼀个向量,找到其同 ⽅向上模为 1 的向量并不难,只要让向量的各成分分别除以向量模⻓就好了。
例如,上⾯的基可以变为$e_i’ = [\frac{1}{\sqrt{2}}\quad \frac{1}{\sqrt{2}}]^T$和$e_j’ = [-\frac{1}{\sqrt{2}}\quad \frac{1}{\sqrt{2}}]^T$。
现在,我们来⽤上⾯的⽅法求取向量$u = [4 \quad 5]^T$在这组新基上的新坐标。那么根据向量内积的⼏何意义,我们只要分别计算$u = [4 \quad 5]^T$和这两个基向量$e_i’ = [\frac{1}{\sqrt{2}}\quad \frac{1}{\sqrt{2}}]^T$和$e_j’ = [-\frac{1}{\sqrt{2}}\quad \frac{1}{\sqrt{2}}]^T$的内积即可,不难得到:
\[u · e_i' = \frac{9}{\sqrt{2}}, u·e_j' = \frac{1}{\sqrt{2}}\]向量的坐标是指定基的对应系数,因此向量 u 的表达式可以写作:
\[\frac{9}{\sqrt{2}}e_i' + \frac{1}{\sqrt{2}}e_j'\]在该基底下,坐标表示为:
\[[\frac{9}{\sqrt{2}} \quad \frac{1}{\sqrt{2}}]^T\]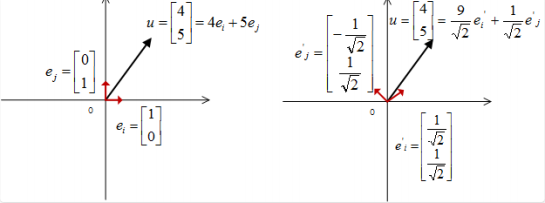
基底的特殊性
不是任何向量都能选作基底
n 维空间中的基底必须满⾜这样的要求:n 维空间中任意⼀个向量都可以表⽰为基向量的线性组合,并且这种线性组合的表⽰⽅式必须是唯⼀的。
基底中的向量数量要⾜够
三维空间中的⼀组基,⾸先每⼀个基向量的维 数必然为 3,而基向量的个数也必须为 3 个。
基向量满⾜线性⽆关
向量线性⽆关的概念,⼀组向量需要满⾜线性⽆关的条件,即:其 中任何⼀个向量都不能通过其余向量的线性组合的形式进⾏表⽰。
当且仅当$x_1 = x_2 = … = x_n = 0$时,线性组合$x_1u_1 + x_2u_2 + x_3u_3 + … + x_nu_n$才能⽣成 0 向量,如果$x_i$中有⾮ 0 值存在,那么这⼀组向量就是线性相关的了。
证明:
对于⼀组线性⽆关的向量$u_1, u_2, …, u_n$ ,对于空间中的向量 p,假设有两种不同的表⽰⽅法,即:
\[p = c_1u_1 + c_2u_2 + ... + c_nu_n = d_1u_1 + d_2u_2 + ... + d_nu_n\]整理一下有:
\[(c_1 - d_1)u_1 + (c_2 - d_2)u_2 + ... + (c_n - d_n)u_n = 0\]由于$u_1, u_2, …, u_n$是线性无关的向量, 那么则必须满足:
\[c_1 - d_1 = 0, c_2 - d_2 = 0, c_n - d_n = 0\]即 $c_i = d_i$,因此就不可能有两种线性组合的表达⽅式,从而产⽣了⽭盾。通过反证法就证明了线性⽆关性和唯⼀性是等价 的。
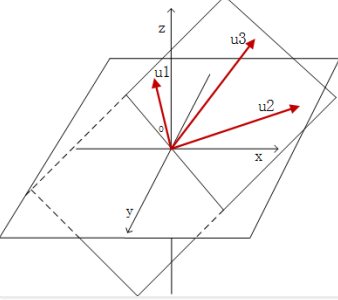
在这个三维空间中,我们就要求所选取的三个基向量线性⽆关,如果它们线性相关,那么$u_3$就可以表⽰为$u_1$和$u_2$的线性组合,换句话说,候选的三个向量就处在⼀个平⾯上了,⾃然⽆法通过线性组合的⽅式表⽰三维空间中的所有向量。
n 维空间不等价于$R^n$空间
2 维空 间不仅仅只有 xoy ⼆维平⾯这⼀种情况,⼀个倾斜在 3 维空间中的过原点的平⾯依然能被称为 2 维空间。更⾼维的空间中同样也会包含 2 维空间。
谈及 2 维空间的⼀组基,不要仅仅就觉得是两个线性⽆关的⼆维向量: $\begin{bmatrix}x_1 \ y_1\end{bmatrix}$和 $\begin{bmatrix}x_2 \ y_2\end{bmatrix}$
张成(span)空间
对于⼀组向量,它的所有线性组合所构成的空间就称之为这⼀组向量的张成空间。
第⼀种情况:
\[u_1 = \begin{bmatrix}1 \\ 1\end{bmatrix}, u_2 = \begin{bmatrix}0 \\ 1 \end{bmatrix}\]向量$u_1$和$u_2$是两个线性⽆关的⼆维向量,它构成了⼆维空间$R^2$的⼀组基,因此它的张成空间就是整个⼆维空间$R^2$。
第⼆种情况:
\[u_1 = \begin{bmatrix}1 \\ 1\end{bmatrix}, u_2 = \begin{bmatrix}-1 \\ -1 \end{bmatrix}\]$u_1 = -u_2$, 因此$u_1$和$u_2$是线性相关的共线向量,它们张成的空间是⼀条穿过原点的⼀维直线。
第三种情况:
\[u_1 = \begin{bmatrix}1 \\ 1 \\ 1 \end{bmatrix}, u_2 = \begin{bmatrix} 1 \\ -1 \\ 1 \end{bmatrix}\]$u_1$和$u_2$两个三维向量线性⽆关,但是由于向量的个数只有两个,因此它们的张成空间是三维空间中的⼀个穿过原点的平 ⾯。
第四种情况:
\[u_1 = \begin{bmatrix}1 \\ 1 \\ 1 \end{bmatrix}, u_2 = \begin{bmatrix} 1 \\ -1 \\ 1 \end{bmatrix}, u_3 = \begin{bmatrix} 3 \\ -1 \\ 3 \end{bmatrix}\]虽然向量的个数是 3,但是$u_3 = u_1 + 2u_2$ ,因此它们是三个线性相关的共⾯向量,张成的空间仍然直是三维空间中的⼀个 穿过原点的平⾯。
第五种情况:
\[u_1 = \begin{bmatrix}1 \\ 1 \\ 1 \end{bmatrix}, u_2 = \begin{bmatrix} 1 \\ -1 \\ 1 \end{bmatrix}, u_3 = \begin{bmatrix} 3 \\ -1 \\ 5 \end{bmatrix}\]三个向量线性⽆关,构成三维空间$R^3$中的⼀组基,因此它们的张成空间是整个三维空间$R^3$。
QA
Q1: 外积的那个计算结果比较难记,有什么计算的技巧吗?
A1:
Q2: 张成空间是不是由向量组合成的矩阵的秩决定?
A2: