改变空间位置:矩阵乘以向量的本质
- 矩阵在左,列向量在右,矩阵的列数和列向量的维数必须相等
- 矩阵和向量相乘的结果也是⼀个向量
- 矩阵的⾏数就是最终结果输出的列向量的维数
- 乘法的规则如上所⽰,就是矩阵的每⾏和列向量进⾏对应元素分别相乘后相加
1
2
3
4
5
6
7
8
9
import numpy as np
A = np.array([[1, 2],
[3, 4],
[5, 6]])
x = np.array([[4, 5]]).T
print(np.dot(A,x))
从结果看,原始向量表⽰⼆维空间中的⼀个点,坐标为 (4,5),经过矩阵$\begin{bmatrix}1 & 2 \ 3 & 4 \ 5 & 6\end{bmatrix}$乘法的作⽤,转化为三维空间中坐标为 (14,32,50) 的点。
在特定矩阵的乘法作⽤下,原空间中的向量坐标,被映射到了⽬标空间中 的新坐标,向量的空间位置(甚⾄是所在空间维数)由此发⽣了转化。
从⾏的⻆度思考
矩阵与向量的乘法如果从⾏的⻆度来看就是向量点乘。
\[Ax = \begin{bmatrix}row_1 \\ row_2\end{bmatrix}x = \begin{bmatrix}row_1 ·x \\ row_2·x\end{bmatrix}\]列的⻆度:重新组合矩阵的列向量
从列的⻆度来看,矩阵 A 与向量 x 的乘法是对矩阵 A 的各列向量进⾏线性组合的过程,每个列向量的组合系数就是向 量 x 的各对应成分。
\[Ax = \begin{bmatrix}a & b \\ c & d\end{bmatrix}\begin{bmatrix}x_1 \\ x_2\end{bmatrix} = x_1\begin{bmatrix}a \\ c\end{bmatrix} + x_2\begin{bmatrix}b \\ d\end{bmatrix} = \begin{bmatrix}ax_1 + bx_2 \\ cx_1 + dx_2\end{bmatrix}\]进⼀步引申:变换向量的基底
二维向量$\begin{bmatrix}x \ y\end{bmatrix}$的坐标是x和y, 它的坐标基于的是默认基底$\begin{bmatrix}1 \ 0\end{bmatrix}$和$\begin{bmatrix}0 \ 1\end{bmatrix}$。 那么二维向量的完整表达式:
\[\begin{bmatrix}x \\ y\end{bmatrix} = x\begin{bmatrix}1 \\ 0\end{bmatrix} + y \begin{bmatrix}0 \\ 1\end{bmatrix}\]我们将矩阵与向量的乘法表达式做进一步展开:
\[\begin{bmatrix}a & b \\ c & d\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix} = \begin{bmatrix}a & b \\ c & d\end{bmatrix}(x\begin{bmatrix}1 \\ 0\end{bmatrix} + y \begin{bmatrix}0 \\ 1\end{bmatrix}) = x\begin{bmatrix}a & b \\ c & d\end{bmatrix}\begin{bmatrix}1 \\ 0\end{bmatrix} + y\begin{bmatrix}a & b \\ c & d\end{bmatrix}\begin{bmatrix}0 \\ 1\end{bmatrix} = x\begin{bmatrix}a \\ c\end{bmatrix} + y\begin{bmatrix}b \\ d\end{bmatrix}\]在矩阵$\begin{bmatrix}a & b \ c & d\end{bmatrix}$的乘法作用下, 向量的基地进行了变换。
映射钱由旧的基底分别乘以对应的坐标$(x, y)$来表示其位置, 而映射后向量自然应该用新的基底来分别乘以对应坐标$(x, y)$来描述改变后的空间位置:
\[x\begin{bmatrix}1 \\ 0\end{bmatrix} + y\begin{bmatrix}0 \\ 1\end{bmatrix} \Rightarrow x \begin{bmatrix}a \\ c\end{bmatrix} + y \begin{bmatrix}b \\ d\end{bmatrix} = \begin{bmatrix}ax + by \\ cx + dy\end{bmatrix}\]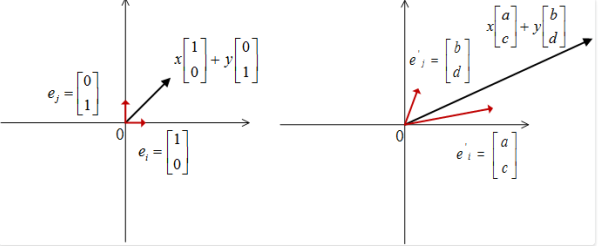
矩阵的各列就是映射后的新基底
扩展到三阶⽅阵
\[\begin{bmatrix}a & b & c \\ d & e & f \\ g & h & i\end{bmatrix}\begin{bmatrix}x \\ y \\ z\end{bmatrix} = \begin{bmatrix}a & b & c \\ d & e & f \\ g & h & i\end{bmatrix}(x\begin{bmatrix}1 \\ 0 \\ 0\end{bmatrix} + y\begin{bmatrix}0 \\ 1 \\ 0\end{bmatrix} + z\begin{bmatrix}0 \\ 0 \\ 1\end{bmatrix}) = x\begin{bmatrix}a \\ d \\ g\end{bmatrix} + y\begin{bmatrix}b \\ e \\ h\end{bmatrix} + z\begin{bmatrix}c \\ f \\ c\end{bmatrix}\]方阵的第一列$\begin{bmatrix}a \ d \ g\end{bmatrix}$是原始基向量$\begin{bmatrix}1 \ 0 \ 0\end{bmatrix}$映射后的新的基向量, 方阵的第二列$\begin{bmatrix}b \ e \ h\end{bmatrix}$是原始基向量$\begin{bmatrix}0 \ 1 \ 0\end{bmatrix}$映射后的新的基向量,方阵的第三列$\begin{bmatrix}c \ f \ i\end{bmatrix}$是原始基向量$\begin{bmatrix}0 \ 0 \ 1\end{bmatrix}$映射后的新的基向量。
基变换的意外情况
“经过矩阵变换,会将原 始的基底变换成为⼀组新的基底”这句话的表述就并不准确。对于⼀个 m×n 的矩阵 A 和 n 维列向量 x,经过 Ax 的乘法作⽤,x 的 n 个 n 维默认基向量构成的基底被 转换成了 n 个 m 维的⽬标向量。
- 当 n>m 的时候,这 n 个向量线性相关,因此不构成基底;
- 当 n<m 的时候,即使这 n 个向量线性⽆关,由于它们不能表⽰ m 维空间中的所有向量,因此也不能称之为基底;
- 当且仅当 n=m,且这 n 个向量线性⽆关的时候,它们才能称之为⼀组新的基底。