⾏压缩数据降维
我们直接从矩阵A的奇异值分解:$A = U \Sigma V^T$入手, 分析如何进行压缩数据降维。
等式两侧同时乘以左奇异矩阵的转置: $U^T$, 得到:
\[U^T A = U^T U \Sigma V^T = \Sigma V^T\]重点是左侧的$U^T A$, 我们把矩阵A记作n个m维列向量并排放置的形式, 我们展开来看:
\[\begin{bmatrix}u_1 & u_2 & ... & u_m\end{bmatrix}^TA = \begin{bmatrix}u_1^T \\ u_2^T \\ ... \\ u_m^T\end{bmatrix}\begin{bmatrix}colA_1 & colA_2 & ... & colA_n\end{bmatrix} = \begin{bmatrix}u_1^TcolA_1 & u_1^TcolA_2 & ... & u_1^TcolA_n \\ u_2^TcolA_1 & u_2^TcolA_2 & ... & u_2^TcolA_n \\ ... & ... & ... & ... \\ u_m^TcolA_1 & u_mcolA_2 & ... & u_m^TcolA_n \end{bmatrix}\]这是基变换方法。
$colA_i$原本使用的是默认的一组基向量$\begin{bmatrix}e_1 & e_2 & … & e_m\end{bmatrix}$, 我们通过上面的基变换, 将其用$\begin{bmatrix}u_1 & u_2 & … & u_m\end{bmatrix}$这一组标准正交基来表示, 由于$AA^T$这⼀组标准正交基本质上也是由协⽅差对称矩阵 得到,因此将各列做基变换后,数据分布从⾏的⻆度来看就彼此⽆关了。
此时,我们可以把每⼀列看作是⼀个样本,各⾏是不同的特征,各⾏彼此⽆关,我们可以按照熟悉的⽅法,选择最⼤的 k 个 奇异值对应的 k 个标准正交向量,形成⾏压缩矩阵:
\[U_{k \times m}^T = \begin{bmatrix}u_1 \\ u_2^T \\ ... \\ u_k^T\end{bmatrix}\]思考:为什么是$k \times m$?
因为U是通过计算协方差对称矩阵$\frac{1}{n-1}AA^T$的特征向量得到的, 维度是$m \times m$。
通过
\[U^T_{k \times m} colA_i = \begin{bmatrix}u_1^T colA_i \\ u_2^T colA_i \\ ... \\ u_k^T colA_i\end{bmatrix}\]就实现了列向量从 m 维到 k 维的数据降维,完成了主成分的提取。
列压缩数据降维
奇异值分解的精彩之处就在于它可以从两个维度进⾏数据降维,分别提取主成分,前⾯介绍的是对⾏进⾏压缩降维,那么下 ⾯我们来说说如何对列进⾏压缩降维。
还是牢牢抓住$A = U \Sigma V^T$进⾏启发,我们对式⼦两边同时乘以右奇异矩阵 V,得到 $AV = U \Sigma$,我们还是聚焦等式的左 侧:AV。
我们将其整体进⾏转置的预处理,得到$(AV)^T = V^TA^T$ ,我们把矩阵 A 记作
\[\begin{bmatrix}row A_1^T \\ row A_2^T \\ ... \\ row A_m^T\end{bmatrix}\]思考:为什么记作$rowA_i^T$?
这其实表示的就是$A^T$的每一行。
那么同样的道理:
\[V^T A^T = \begin{bmatrix}v_1^T \\ v_2^T \\ ... \\ v_n^T\end{bmatrix}\begin{bmatrix}rowA_1 & rowA_2 & ... & rowA_m\end{bmatrix} = \begin{bmatrix}v^TrowA_1 & v_1 rowA_2 & ... & v_1^T rowA_m \\ v_2 rowA_1 & v_2^T row A_2 & ... & v_2 row A_m \\ ... & ... & ... & ... \\ v_n^T rowA_1 & v_n^T row A_2 & ... & v_n^T row A_m \end{bmatrix}\]类⽐上⾯的⾏压缩过程,在 V 中,我们从⼤到小取前 k 个特征值对应的标准正交特征向量,就构成了另⼀个压缩矩阵:
\[V_{k \times n}^T = \begin{bmatrix}v_1^T \\ v_2^T \\ ... \\ v_k^T\end{bmatrix}\]很明显,通过$V_{k \times n}^T A^T$就能实现将$A^T$矩阵的各列由 n 维压缩到 k 维。而⼤家不要忘了, $A^T$的列不正是 A 矩阵的各⾏吗。
由此,各⾏向量的维数由 n 压缩到了 k 维,实现了列压缩的数据降维。
对矩阵整体进⾏数据压缩
这⾥我们不谈按⾏还是按列,我们从矩阵的整体视⻆,再谈⼀个数据压缩的⽅式,我们的思路有点类似级数的概念,将⼀个$m \times n$的原始数据矩阵 A 分解成若⼲个同等维度矩阵乘以各⾃权重后相加的形式。
依旧从奇异值分解的表达式⼊⼿, $A = U \Sigma V^T$,我们展开成完整的矩阵形式:
\[A = \begin{bmatrix}u_1 & u_2 & ... & u_m\end{bmatrix} \begin{bmatrix}\sigma_1 & & & & \\ & \sigma_2 & & & \\ & & ... & & \\ & & & \sigma_r & \\ & & & & \\ & & & &\end{bmatrix} \begin{bmatrix}v_1^T \\ v_2^T \\ ... \\ v_n^T\end{bmatrix}\]这⾥展开就得到了:
\[A = \sigma_1 u_1 v_1^T + \sigma_2 u_2 v_2^T + ... + \sigma_r u_r v_r^T\]不难发现,每⼀个$u_i v_i^T$的结果都是⼀个等维的$m \times n$形矩阵,并且它们彼此之间正交,前⾯的$\sigma_i$则是对应矩阵的权重,$\sigma_1 > \sigma_2 > \sigma_3 > … > \sigma_r$, 依序代表了“重要性”的程度,因此我们可以按照主成分贡献率的最低要求,选择前 k 项进⾏叠加, ⽤来对原始数据矩阵 A 进⾏近似:
\[A \Rightarrow \sigma_1 u_1 v_1^T + \sigma_2 u_2 v_2^T + ... + \sigma_k u_k v_k^T\]思考:为什么奇异值/特征值可以决定主成分贡献率。
因为在讲协方差对称矩阵转化成对角矩阵后,对角线上的元素既是特征值/奇异值, 又是方差。
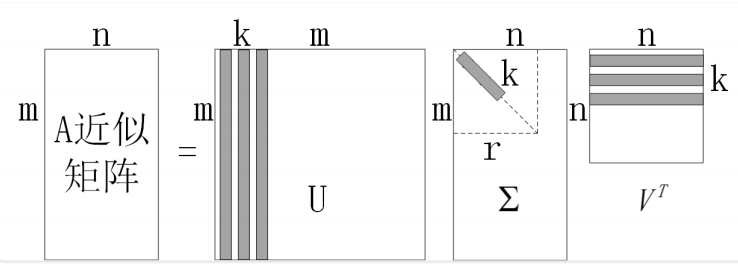
原理⽰意图如图⽰:
QA
Q:为什么奇异值/特征值可以决定主成分贡献率?
Q: 这个矩阵近似是不是相当于行列同时压缩?
Q:之前特征值分解压缩时我们可以理解为压缩特征,如果单独用右奇异矩阵进行列压缩,是不是压缩了样本数量,有什么意义
Q:行和列压缩的效果该怎么看