谈谈$\Delta y$与$dy$
⾸先我们还是来看导数的含义,如果函数 f(x) 在点$(x_0, y_0)$处是可微的,那么依照定义就有:
\[\lim_{\Delta x \rightarrow 0}\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = f'(x_0)\]$\Delta x$的值越小,越趋近于0, $\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}$就越趋向于$x_0$处导数的真实值$f’(x_0)$。
对式子进行变换:
\[f(x_0 + \Delta x) - f(x_0) \approx \Delta x f'(x_0)\]这个表达式的左侧部分$f(x_0 + \Delta x) - f(x_0)$乘坐$\Delta y$, 顾名思义就是当自变量x从$x_0$变到$x_0 + \Delta x$时, y的真实改变量, 而右侧部分$\Delta x f’(x_0)$我们称之为dy, 它充当的是$\Delta y$的近似值,如图所示:
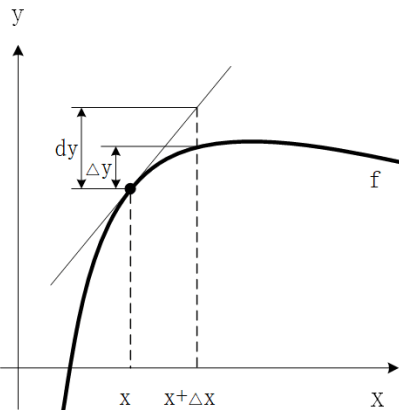
因此, dy可以作为$\Delta y$的一个近似值来看待, 特别是当$\Delta x$越小的时候, 近似效果越好。
对于⾃变量为 x 的可微函数 y=f(x),$\Delta x$ 、$dx$ 、$\Delta y$ 、$dy$ 的含义分别总结如下:
- $\Delta x$: 表示自变量x的任意增量。
- $dx$:表示自变量x的微分, 实际上就等于$\Delta x$。
- $\Delta y$: 表⽰当⾃变量 x 变化到$dy = f’(x)dx$时,因变量 y 的真实改变量,即:$\Delta y = f(x + \Delta x) - f(x)$ 。
- $dy$:因变量y的微分, 实际上$dy = f’(x)dx$, 微分 dy 可以作为真实值$\Delta y$的⼀个近似。
因此可以看出,微分的作⽤⾮常⼴,我们这⾥⾸要关⼼的就是它在近似过程中的应⽤:
\[f(x + \Delta x) = f(x) + \Delta y \approx f(x) + dy = f(x) + f'(x) \Delta x\]线性近似的概念
基于上⾯的式⼦,进⼀步的,我们可以表⽰出:假如函数 f 在 c 点处可微,由直线⽅程的写法可以拿出函数 f 的曲线在点 (c,f(c)) 处的切线⽅程 g(x):
\[f'(c) = \frac{g(x) - f(c)}{x - c} \Rightarrow g(x) = f(c) + f'(c)(x - c)\]那么此时,过点 (c,f(c)) 的切线 g(x) 就可以看做是原函数 f 在点 c 处的线性近似.
我们试着⽤上⾯的⽅法来观察⼀下函数 f(x)=1+sin2x 在取值$x = \pi / 2$处的线性近似情况。
我们⾸先按照上⾯的公式写出$x = \pi / 2$处的切线⽅程:
\[g(x) = f(c) + f'(c)(x - c) = f(\pi / 2) + f'(\pi / 2)(x - \pi / 2) \\ = 1 + sin \pi + 2 cos \pi (x - \pi / 2) = -2 x + (1 + \pi)\]即:$g(x) = -2x + (1 + \pi)$
然后我们绘制出$f(x)$和$x = \pi / 2$处切线的图像, 并在不同的自变量区域尺度内观察:
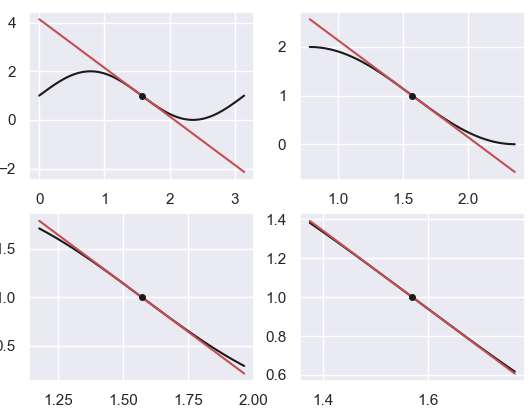
很明显的是,随着⾃变量 x 区间的不断收窄,在点$(\pi/2, f(\pi))$的领域附近,切线的图像和原函数是⾼度重合的,因此在 越来越小的时候,线性近似的效果就会显得越好。
关于⽆穷级数
⽆穷级数的前 n 项和
这⾥我们引⼊⼀个背景知识进⾏讨论。当我们⽤计算机来计算正余弦函数或者是⾃然对数的幂,即$e^n$的时候,通常是基于下⾯的⽆穷数列来给出满⾜较⾼精度的近似值:
\[sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + ...\] \[cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + ...\] \[e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + ...\]上⾯的表达式就是⽆穷级数。⽆穷级数的概念很多,我们先看最简单的:⼀组数字的⽆穷级数:
\[\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ...\]在这个级数当中,如果只包含第⼀项,那么和就为 1/2,如果包含前两项,那么和为 1/2+1/4=3/4,如果只包含前三项,那么和就为$1/2 + 1/4 + 1/8 = 7/8$。
级数的前有限项的和,我们叫作部分和。我们把前 n 项部分和记为是$S_n$,很显然对照上⾯所描述的就有:
\[S_1 = \frac{1}{2}, S_2 = \frac{3}{4}, S_3 = \frac{7}{8}\]还可以归纳出 $S_n = 1 - \frac{1}{2^n}$,并且可以看得出, $S_n$ 收敛于 1。
而⾄于说⽆穷级数的和,我们将其定义为部分和$S_n$的极限:
\[\lim_{n \rightarrow \infty} S_n\]当然,我们脱离上⾯这些个具体的数字来谈定义,我们给出⽆穷级数前 n 项和的⼀般表⽰⽅法,即考虑⽆穷级数:
\[a_1 + a_2 + a_3 + a_4 + a_5 + ...\]那么在这种表示方法之下, 前n项的和定义为:
\[S_n = a_1 + a_2 + a_3 + ... + a_n = \sum_{k=1}^{n} a_k\]级数的收敛性
对于⼀个⽆穷级数$\sum_{k=1}^\infty a_k$ ,如果由它的前 n 项和构成的数列$S_1, S_2, S_3, …, S_n$最终收敛于 S,那么我们就称⽆穷级数 $\sum_{k=1}^\infty a_k$ 收敛并且它的和为 S。反之,如果数列$S_1, S_2, S_3, …, S_n$发散,那么⽆穷级数也是发散的,这个⽆穷级数是没有和的。
⼏何级数
对于⽆穷级数,我们特别地需要关注以下这种形式:
\[\sum_{k=1}^\infty a r^{k-1} = a + ar + ar^2 + ar^3 + ...\]其中$a \neq 0$。
这种形式所表⽰的级数,称之为⼏何级数,这是⼀种⽐较常⻅的级数。更具体的,我们可以把⼏何级数划分为两⼤类。
⼀类是常数项级数,即不含⾃变量的,类似于:
\[\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + ...\]也就是上⾯写的$\sum_{n=1}^{\infty} a_n$这种形式。
另外⼀类就是函数项的级数,即$\sum_{n=1}^{\infty}a_n(x)$ 。这其中,级数的每⼀项$a_n(x)$都是⼀个关于⾃变量 x 的函数,函数项的级数⽤处更为⼴泛,它将是我们后续内容中的重点研究的对象。
最基本、最简单的⼀种函数项⽆穷级数:
\[\sum_{n=0}^{\infty}a_n x^n = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + ...\]我们就将其称之为⾃变量 x 的幂级数。而进⼀步,我们将这种表达式⼀般化,写成是:
\[\sum_{n=0}^\infty a_n (x - a)^n = a_0 + a_1(x - a) + a_2(x - a)^2 + a_3(x - a)^3 + ...\]这称为关于 x-a 的幂级数。
函数的幂级数表⽰及其近似
利⽤泰勒级数表⽰函数
我们是想探究这样⼀个问题,那就是给定⼀个已知函数 f(x),我们能否将这个函数以 x-a 的幂级数的形式进⾏ 表⽰,并且探索它的⼀些重要性质?
那么,更具体的,我们的⽬标就是找到⼀组数$c_0, c_1, c_2,…, c_n$,使得函数 f(x) 表达成如下的形式:
\[f(x) = c_0 + c_1(x - a) + c_2(x - a)^2 + c_3(x - a)^3 + ...\]如果这个式⼦想要成⽴,很显然,我们对上⾯的级数表达式进⾏求导,从⼀阶导数开始,逐步求取它的⾼阶导数( n 阶 导):
\[f(x) = c_0 + c_1(x - a) + c_2(x - a)^2 + c_3(x - a)^3 + ...\] \[f'(x)=c_1+2c_2(x-a) + 3c_3(x-a)^2+4c_4(x-a)^3+...\] \[f'’(x)=2\times 1c_2+3\times 2c_3(x-a)+4\times 3c_4(x-a)^2+...\] \[f^{(3)}(x)=3\times 2\times 1c_3+4\times 3\times 2c_4(x-a)+5\times 4\times 3c_5(x-a)^2...\] \[f^{(4)}(x)=4\times 3\times 2\times 1c_4+5\times 4\times 3\times 2c_5(x-a)...\]看上去⼀⼤篇的式⼦,我们⼜该如何处理呢?其实也很容易,我们将 x=a 代⼊到上⾯的所有表达式中,就可以顺利地消去所 有的⾮常数项:
\[f(a)=c_0\Rightarrow c_0=f(a)\] \[f'(a)=c_1\Rightarrow c_1=f'(a)\] \[f'’(a)=2\times 1c_2\Rightarrow c_2=\frac{f''(a)}{2!}\] \[f^{(3)}(a)=3\times 2\times 1c_3 \Rightarrow c_3=\frac{f^{(3)}}{3!}\] \[f^{(4)}(a)=4\times 3\times 2\times 1c_4 \Rightarrow c_4=\frac{f^{(4)}}{4!}\]最后,我们可以得出系数$c_n$的⼀般表达形式:
\[c_n = \frac{f^{(n)}(a)}{n!}\]从这个推导过程中,我们知道了函数 f(x) 如果能⽤关于 (x-a) 的幂级数的形式来进⾏表⽰,那么表达的⽅式不可能多于⼀ 种。那么,对于⼀个给定函数 f(x) 而⾔,⽤以 (x-a) 为表达⽅式的幂级数,我们就将其称之为 泰勒级数 ,而⼀种⽐较特殊的情况,即当 a=0 时的幂级数,我们可以将其称之为麦克劳林级数。
如果我们把泰勒级数的项数固化到 n 项,会更⽅便于我们在实际过程中的处理,毕竟我们不可能处理⽆限个级数项。这⾥我们运⽤微分中值定理,就可以把⽆穷 项的泰勒级数转化为有限项的泰勒级数,这⾥运⽤到的就是带有余项的泰勒公式,即如果函数f(x) 的 (n+1) 阶导数$f^{(n+1)}$在 x=a 的邻域内存在,那么在这个邻域内函数 f 可以表⽰成以下的有限项的形式:
\[f(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + ... + \frac{f^{(n)}(a)}{n!}(x - a)^n + R_n(x)\]最后⼀项$R_n(x)$我们称之为余项,换句话说它代表了函数真实值 f(x) 与前 n 项和之间的误差,利⽤微分中值定理,我们可 以将其表⽰为:
\[R_n(x) = \frac{f^{(n + 1)}(c)}{(n+1)!}(x - a)^{n+1}\]在这其中, c 是 x 和 a 之间的⼀点。
函数的泰勒近似
我们可以利⽤函数 f 的泰勒级数的前 n 项和来对函数在 x=a 邻域内的实际取值进⾏ 近似。
再回过头来看看前⾯对于函数的线性近似的内容,我们讲过函数 f 在 a 点邻域内的值,可以⽤经过函数 f 点 (a,f(a)) 的切线 去近似:
\[p_1(x) = f(a) + f'(a) (x - a)\]看看这是什么?我们发现 由两项组成,即包含泰勒级数关于 x=a 点展开的 0 阶项和 1 阶项,因此,我们把线性近似称之为是⼀阶泰勒多项式。
但是我们不难发现,毕竟切线是⼀条直线,⽤它去近似函数 f 所代表的曲线,只要随着⾃变量 x 稍微远离 a 点,近似值和实 际的函数取值的差距就会显著增⼤。
于是我们就在想,线性近似只使⽤了泰勒级数的第 0 项和第 1 项,似乎丢失了太多后⾯的信息,那么我们把级数中后续更⾼ 阶的项也利⽤起来,例如⽤ 2 阶泰勒多项式:
\[p_2(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2\]这个相⽐于⼀阶泰勒多项式(也就是线性近似),它的近似效果会显得更好。 如果我们追求更⾼的近似精度,我们可以使⽤更⾼阶数的 n 阶泰勒多项式进⾏函数的近似:
\[p_n(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + ... + \frac{f^{(n)}(a)}{n!}(x - a)^n\]并且相应地,如果此时 a=0 ,那么 n 阶泰勒多项式就转化为了 n 阶麦克劳林多项式,⽤于对 0 附近邻域内的函数取值进⾏ 近似。
\[f(x) \approx p_n(x) = f(0) + f'(0)x + \frac{f''(x)}{2!}x^2 + ... + \frac{f^{(n)}(0)}{n!}x^n\]