⼆元函数的可视化

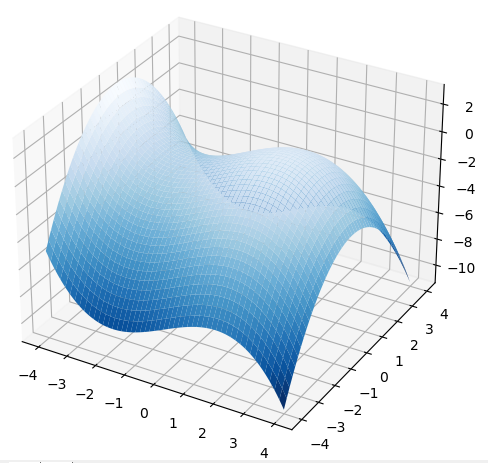
下⾯，我们来实践⼀下如何利⽤ Python 来绘制三维曲⾯：$z = x - \frac{1}{9} x^3 - \frac{1}{2}y^2$ 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from matplotlib import pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = Axes3D(fig)

x = np.arange(-4, 4, 0.01)
y = np.arange(-4, 4, 0.01)
x, y = np.meshgrid(x, y)
z = x - (1./9) * x ** 3 - (1. / 2) * y ** 2

ax.plot_surface(x, y, z, cmap=plt.cm.Blues_r)
plt.show()

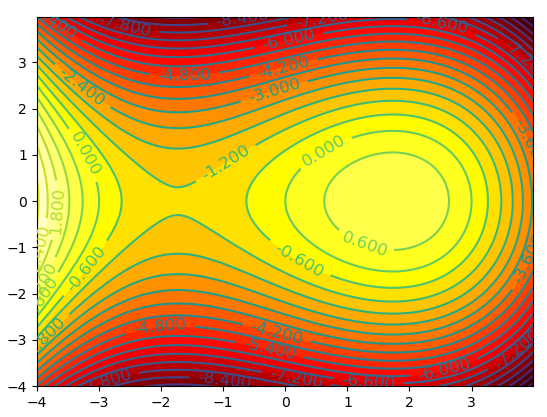
等⾼线图的绘制

在三维图形的绘图中，还有⼀种呈现三维图形性质的表⽰⽅法，那就是等⾼线图。等⾼线图⼤家不会陌⽣，它的定义是，利 ⽤每⼀个⽔平⾯ z=c 与函数图形表⾯相交于⼀条曲线，然后将所有的这些曲线投影到 xoy 平⾯上，就得到不同⾼度（也就是 z=f(x,y)）取值的等⾼线集合，即构成了这个三维图形的等⾼线图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
import matplotlib.pyplot as plt

def f(x, y):
    return x - (1. / 9) * x ** 3 - (1. / 2) * y ** 2


x = np.arange(-4, 4, 0.01)
y = np.arange(-4, 4, 0.01)

# 把x， y数据生成mesh网格状的数据
X, Y = np.meshgrid(x, y)

# 填充等高线间的颜色
plt.contourf(X, Y, f(X, Y), 24, cmap=plt.cm.hot)
# 添加等高线
C = plt.contour(X, Y, f(X, Y), 24)
# 增加各等高线的高度值
plt.clabel(C, inline=True, fontsize=12)

plt.show()

多元函数的偏导数

概念的引⼊

假如函数 f(x,y) 是关于 x 和 y 两个变量的函数，我们在讨论导数概念的时候需要固定⼀个变量再去讨论另外⼀个变量。例 如，我们需要先将 y 固定为⼀个常数 $y = y_0$，此时$f(x, y_0)$实际上就变成了⼀个只有单个变量 x 的函数，那么它在$x = x_0$处的导数称为是 f 关 于x 在 $(x_0, y_0)$处的偏导数，被记作是： $f_x(x_0, y_0)$。

那么按照我们之前利⽤极限来定义导数的式⼦进⾏迁移拓展，我们很容易得到偏导数的定义式，即：

那么同样地，函数 f(x,y) 关于 y 在$(x_0, y_0)$ 处的偏导数，记作是：

和导数中的线性算⼦$\frac{d}{dx}$类似，偏导数中也有⾃⼰的特⾊符号$\partial$ ，那么$\frac{\partial}{\partial x}$和 $\frac{\partial}{\partial y}$则分别表⽰对 x 和 y 求偏导的线性算⼦。

那么，针对多元函数 z=f(x,y)，下⾯的这⼀系列描述都是等效的：

针对$(x_0, y_0)$的具体取值$f_x(x_0, y_0)$ ，则可以记作是：

偏导数的⼏何意义

我们还是来看$z = x - \frac{1}{9}x^3 - \frac{1}{2}y^2$这个⼆元函数，来研究⼀下 $\frac{\partial z}{\partial x}$。请⼤家记住，在求关于变量 x 的偏导数时，y 就是⼀个与变量 x ⽆关的常数。

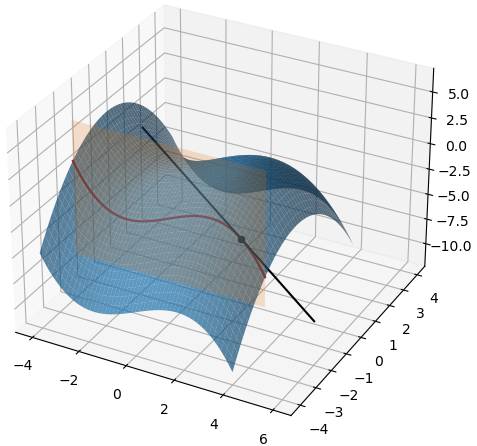
结合下⾯的代码和⽰意图来看$f_x(x_0, y_0)$的⼏何含义。在代码例⼦中，我们实际举例$x_0 = 3, y_0 = -2$，⾸先，我们让 y=- 2这个橙⾊的垂直平⾯与整个蓝⾊曲⾯相交，形成曲⾯表⾯那条红⾊的相交曲线，也就是说这条红⾊曲线既在表⽰原函数的蓝 ⾊曲⾯上，也在平⾏于 xoz 平⾯的橙⾊平⾯ y=-2 上。

我们过点$(x_0, y_0, f(x_0, y_0))$ ，在图中就是那个位于 (3,-2,-2) 的⿊⾊点，做红⾊曲线的切线。那么最终原函数 z 关于 x 的偏导数的取值： $f_x(3, -2)$就是这条切线的斜率，需要注意的是，这条切线同样也在垂直平⾯ y=-2 中，与 xoz 平⾯平⾏.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from matplotlib import pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = Axes3D(fig)

# 多元函数z = f(x, y)
def f(x, y):
    return x - (1. / 9) * x ** 3 - (1. / 2) * y ** 2


# 绘制原函数的图像
x = np.arange(-4, 4, 0.01)
y = np.arange(-4, 4, 0.01)
x, y = np.meshgrid(x, y)
ax.plot_surface(x, y, f(x, y), alpha=0.7)

# 绘制平面y = -2
x = np.arange(-4, 4, 0.01)
z = np.arange(-8, 5, 0.01)
x, z = np.meshgrid(x, z)
y = - 2
ax.plot_surface(x, y, z, alpha=0.2)

# 当确定y0 = -2时， 函数变成了一条平行于xoz平面的曲线
x = np.arange(-4, 4, 0.01)
y = np.array([-2] * len(x))
ax.plot(x, y, f(x, y), color='r')

# 过(3, -2, f(3, -2))， 做上述曲线的切线
# y = -2时， 关于x的偏导数的方程为: z = -2x + 4
ax.scatter(3, -2, f(3, -2), color='k')

x = np.arange(-1, 6, 0.01)
y = np.array([-2] * len(x))
z = -2 * x + 4
ax.plot(x, y, z, color='k')

plt.show()

思考： 为什么y = -2时， 关于x的偏导数的方程为: z = -2x + 4？

回答： $z = x - \frac{1}{9}x^3 - \frac{1}{2}y^2$求导$\frac{\partial z}{\partial x} = 1 - \frac{1}{3}x^2$， 代入$x_0 = 3$可得$\frac{\partial z}{\partial x} = -2$, 因此当$y_0 = -2$时， 该点的斜率为-2， 因此$z = -2 x + 4$。

⾼阶偏导数

我们知道，对于多元函数 f(x,y)，⽆论是关于 x 的偏导数 $f_x$：$\frac{\partial f}{\partial x}$ ，还是关于 y 的偏导数 $f_y$：$\frac{\partial f}{\partial y}$ ，实际上仍然也都是函数，是关于变量 x 和 y 的函数。 因此这些偏导函数再对变量 x 和 y 进⼀步求偏导，就能够得到阶数更⾼的偏导数，也就是函数 f 的⼆阶偏导数，显然⼆元函 数 f(x,y) 的⼆阶偏导数有四个：

多元函数的极限与连续

多元函数极限的概念

和⼀元函数相⽐，多元函数极限的概念要相对⿇烦⼀点：

多元函数$f(x, y)$极限的定义义是 f(x,y) 的值在 (x,y) 趋近于 (a,b) 时趋近于 L，但是问题的关键是 (x,y) 趋近于 (a,b) 的⽅式，我们回顾⼀下⼀元函数 f(x) 在 c 点处存在极限的定义，它是要求函数的左极限等于右极限，即：

要求函数的⾃变量从 x 轴的正负两个⽅向分别逼近取值点 c。

那么拓展到⼆元函数 f(x,y)，极限的定义也是⼀样，它需要在平⾯上满⾜ (x,y) ⽆论从哪个⽅向趋近于 (a,b) 都应该得到相同 的 L 值，那么⼆元函数的极限 f(x,y) 就⼀定存在并且为 L。

下⾯这个严格的定义就能够包含这层意思：

如果我们任意给出⼀个很小的值$\epsilon > 0$ ，都存在$\delta > 0$ ，使得当 $0 < \mid (x, y) - (a, b) \mid < \delta$时，$\mid f(x, y) - L\mid < \epsilon$ 成⽴。则称当 (a,b) 趋近于 (x,y) 时，f(x,y) 的极限为 L，我们将其记作是：

多元函数的连续性

我们还是以⼆元函数为例，⾸先抛出满⾜连续性的条件定义，那就是：

结合前⾯的内容和⼀元函数连续性的定义，这⾥⾯包含了两层的关键含义：

• ⾸先就是函数 f 在 (a,b) 处的极限要存在
• 其次函数 f 在 (a,b) 处要有定义，并且其取值要与极限值相等

那么在单点的连续性上，进⼀步讨论区域上的连续性就不那么难了，显然，若函数 f(x,y) 在区域 S 中的每⼀点都连续，那么 我们就称函数 f(x,y) 在区域 S 内连续。

观察：⼆阶偏导数的对称性

那就是如果在区域 S 中$f_{xy}$和$f_{yx}$分别连续，那么在区域 S 内的每⼀点都满⾜$f_{xy}=f_{yx}$ ，换句话说就是函数改变混合偏导数的求导顺序，最终的结果是不变的。这个结论⾮常重要，后⾯在⿊塞矩阵中 我们还会⻅到。

• Previous
  【机器学习】038--函数近似与泰勒级数
• Next
  【机器学习】040--多元函数的微分及泰勒近似