多元函数的可微性讨论
偏导数存在就可微吗
对于⼀个⼀元函数而⾔,函数 f 在 x 处可微意味着函数的导数 f’(x) 存在。那我们可以说对于⼆元函数 f(x,y),只 要函数的偏导数$f_x$和$f_y$存在,就能够说这个⼆元函数 f(x,y) 可微吗?能是这样吗?
我们看函数$z = -5 \sqrt{\mid xy \mid}$的图形:
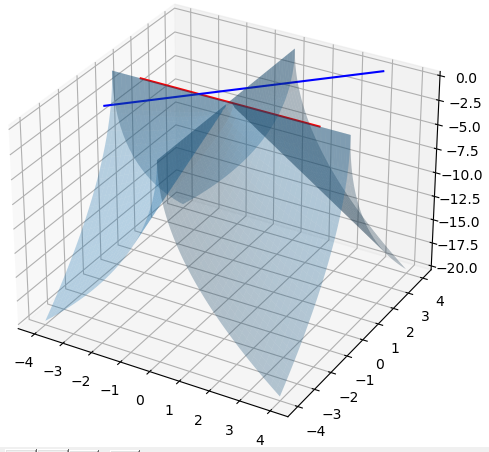
我们只看 (0,0) 这⼀点,在 x 轴和 y 轴⽅向上,偏导数确实都存在,换句话说在沿着 x 轴和 y 轴的邻域内,都有⼀条直线能 够很好的接近邻域内的 f(x,y) 函数取值,但是如果这条直线换到其它⽅向,例如这条蓝⾊的线所在⽅向,(0,0) 的邻域内,蓝⾊的线⽆法做到逼近 (0,0) 两侧的函数值 f(x,y)。
因此,光靠两个偏导数的存在就想定义出多元函数的可微性,显然是不可能的,那我们回想⼀下⼀元函数可微性背后的⼏何 意义。
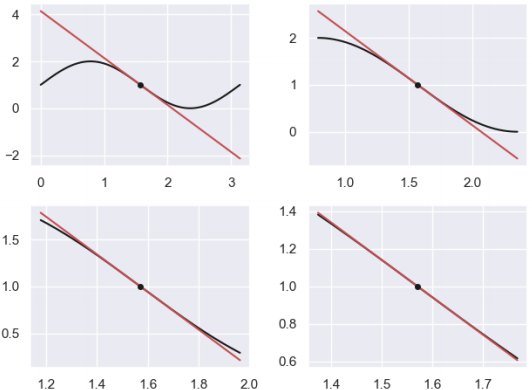
如果函数 f 在点 (a,f(a)) 处可微,在⼏何上意味着存在⼀条切线通过点 (a,f(a)),并且接近在点 a 周围的 x 点邻域内的函数值,也就是我们之前说过的在点 a 附近满⾜线性近似性,借⽤前⾯的⼀张图来复习⼀下:
利⽤切平⾯来描述⼆元函数的可微
⼀元函数下某个点可微的条件,就是存在⼀个切线,来逼近该点邻域内的函数取值。那么拓展到 ⼆元函数 f(x,y),在点$(x_0, y_0, f(x_0, y_0))$满⾜可微的条件,就应该是过该点存在⼀个切平⾯,使得在该点各个⽅向附近的领域内都能很好地逼近 函数 f(x,y) 的取值,这也就是所谓的⼆元函数的局部线性性。
可微性的形式化定义
⼀元函数在点 (a,f(a)) 处的局部线性性是怎么说的?如果存在⼀个常数 m,使得等式 $f(a + h) = f(a) + hm + h \epsilon(h)$成⽴,并且$\epsilon(h)$ 满⾜$\lim_{h \rightarrow 0}\epsilon(h) = 0$ 。如果满⾜上述条件,则说明函数 f 在点 (a,f(a)) 处是满⾜局部线性性的。这⾥⾯的道理我们再简单地解释⼀下,把上⾯的式⼦做简单的变换就有:
\[\epsilon(h) = \frac{f(a + h) - f(a)}{h} - m\] \[\lim_{h \rightarrow 0} \epsilon(h)= \lim_{h \rightarrow 0} \frac{f(a + h) - f(a)}{h} - m = 0\]最终就得到这个式子:
\[\lim_{h \rightarrow 0} \frac{f(a + h) - f(a)}{h} = m\]因此在满⾜局部线性性的条件下,⼀元函数在 a 点处可微就得到了证明。
而拓展到⼆元函数的局部线性性,该如何定义?我们直接拿出定义:
\[f(a + h_1, b + h_2) = f(a, b) + h_1 f_x(a, b) + h_2 f_y(a, b) + h_1 \epsilon_1(h_1, h_2) + h_2 \epsilon_2(h_1, h_2)\]同样地满⾜,当$(h_1. h_2) \rightarrow 0$时:
\[\epsilon_1 (h_1, h_2) \rightarrow 0 , \epsilon_2(h_1, h_2) \rightarrow 0\]这⾥, $h_1$和$h_2$分别作为⼆元变量 x 和 y 的微小增量,因此就囊括了点 (a,b) 附近的各个⽅向上的邻域。它显⽰了在指定点邻域内的各个⽅向上看,函数图像都是“光滑”的,没有“尖峰”的。
最后我们来总结⼀下结论:如果函数 f(x,y) 在点 (a,b) 处呈现出局部线性性,那么函数在该点处就满⾜可微。更进⼀步,如果在⼀个区域内每⼀个点都可微,那么就说函数在这个 区域内都是可微的。
可微性的⼏何意义
函数邻域内的图像
这⾥我们再写成向量形式,⼏何意义就会更加明显⼀些。
我们要讨论的点为:$p_0 = (a, b)$ ,微小增量写成⼀个向量 $h = (h_1, h_2)$,同时令 $\epsilon(h) = (\epsilon_1(h_1, h_2), \epsilon_2(h_1, h_2))$,因此我们把上⾯⼆元函数 f(x,y) 的局部线性性的定义按照向量的形式重写⼀下即为:
\[f(p_0 + h) = f(p_0) + (f_x(p_0), f_y(p_0))·h + \epsilon(h)·h\]这个式⼦中,我们就可以很清晰的看到,向量$h = (h_1, h_2)$就能体现出从任意⽅向进⾏逼近的含义了。
为了更直观的掌握⼆元函数局部线性性的概念,我们还是来看⼀下$z = x - \frac{1}{9}x^3 - \frac{1}{2}y^2$这个例⼦。
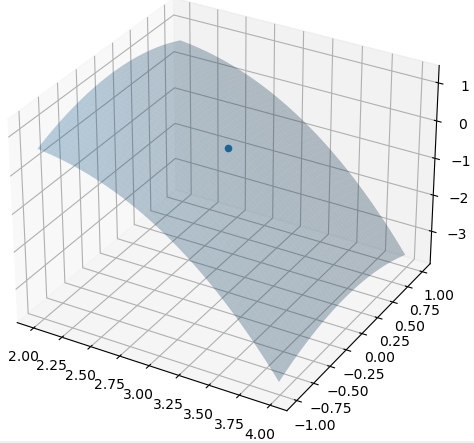
⾸先在变量 x 取 [-4,4],变量 y 取 [-4,4] 范围内的函数图像如下,我们重点关注点 (3, 0, f(3, 0)) 的附近邻域。
⾸先在⼀个较⼤的变量范围内来看,变量 x 取 [2,4],变量 y 取 [-1,1] 范围内:
然后我们缩小邻域的范围,变量 x 取 [2.8,3.2],变量 y 取 [-0.2,0.2] 范围内:
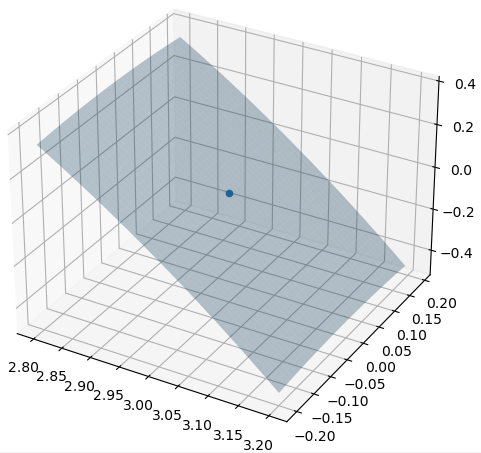
这⾥我们发现,如果函数 f 在某个点可微,那么当邻域范围很小的时候,邻域附近的函数图像近似于⼀个平⾯。
邻域切平⾯与梯度向量
在$f(p_0 + h) = f(p_0) + (f_x(p_0), f_y(p_0))·h + \epsilon(h)·h$这个定义式中,我们发现向量$(f_x(p_0), f_y(p_0))$, 我们 将其称之为函数$f$在$p_0$处的梯度,有专⻔的记号,我们记作为:$\nabla f(p_0)$。
于是此时,表达式
\[f(p_0 + h) = f(p_0) + (f_x(p_0), f_y(p_0))·h + \epsilon(h)·h\]就可以另外写作
\[f(p_0 + h) = f(p_0) + \nabla f(p_0)·h + \epsilon(h)·h\]那么在邻域附近时,也就是当$h \rightarrow 0$时,由于有$\epsilon(h) \rightarrow 0$ ,那么则有:
\[f(p_0 + h) \approx f(p_0) + \nabla f(p_0) · h\]这和我们在⼀元函数中的情形$f(x + \Delta x) \approx f(x) + f’(x) \Delta x$是⼀样的。
也就是说,在⼀元函数中,我们⽤$f(x) + f’(x)\Delta x$所表⽰的切线来对邻域附近的函数值进⾏近似。而在⼆元函数中,我们 使⽤ $f(p_0) + \nabla f(p_0)·h$来对$p_0$的邻域附近的取值$f(p_0 + h)$进⾏近似。很容易联想到$f(p_0) + \nabla f(p_0)·h$应该是个什么。
我们令: $p = p_0 + h$, 那么$g(p) = f(p_0) + \nabla f(p_0)·(p - p_0)$, 这就是过$p_0$点的曲面的切平面, 显然我们就是⽤这个切平⾯的取值 g(p) 来近似曲⾯上$p_0$邻域内 p 的实际取值 f(p)。
实际求解演练
这⾥我们来实际操练⼀下,来求⼀下⼆元函数$f(x, y) = x^2y + xe^y$在点 (2,0) 处的切平⾯。
⾸先,我们求出函数的梯度向量表达式:
\[\nabla f(p) = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}) = (2xy + e^y, x^2 + xe^y)\]那么在点$p_0$也就是 (2,0) 处的梯度值为:
\[\nabla f(p_0) = (2xy + e^y, x^2 + xe^y) = (1, 6)\]最终,我们来写⼀下曲⾯过点 (2,0) 的切平⾯的⽅程:
\[g(p) = f(p_0) + \nabla f(p_0)·(p - p_0)\]转换⼀下:
\[g(x, y) = f(2, 0) + \nabla f(2, 0) · (x - 2, y) = 2 + (1, 6)·(x - 2, y) = 2 + x - 2 + 6y = x + 6y\]即过 (2,0) 点的切平⾯的⽅程我们就通过上述⽅法求得了: f(x,y)=x+6y。
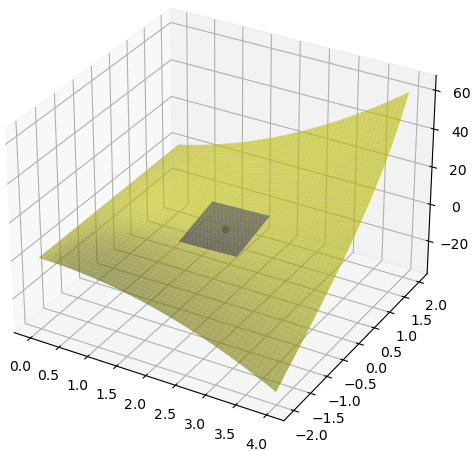
多元微分在近似计算上的应⽤
$dz$ 和 $\Delta z$
我们依据上⾯关于切⾯的表达式 $g(p) = f(p_0) + \nabla f(p_0) · (p - p_0)$,稍做写法上的改变。
我们令$p_0 = (x_0, y_0, z_0)$是相应曲面f(x, y)上的固定点,过点$p_0$的切平⾯⽅程我们写作 z=g(x,y)。那么依据切⾯表达式,整理⼀下就有:
\[z - z_0 = f_x(x_0, y_0)(x - x_0) + f_y(x_0, y_0)(y - y_0)\]同理,我们模拟⼀元函数中的写法,可以把这个等式写成:
\[d_z = f_x(x_0, y_0)dx + f_y(x_0, y_0)dy\]我们知道,对于⾃变量而⾔,$dx = \Delta x$, $dy = \Delta y$,分别表⽰⾃变量 x 和⾃变量 y 上的变化。
而对于因变量z, $dz$和$\Delta z$的含义却截然不同:
\[dz = f_x(x_0, y_0)dx + f_y(x_0, y_0)dy = \nabla f · (dx, dy)\]表⽰的是在这个切平⾯上 z 值的变化。
$\Delta z = f(x, y) - f(x_0, y_0)$表示的是当自变量发生变化时, 函数$f(x, y)$实际发生的变化。
因此,这⾥同⼀元函数的情况是很类似的,当⾃变量的变化 dx 和 dy 的变化⾮常微小的时候,我们就可以拿切平⾯上的 dz 的切平⾯去近似实际的$\Delta z$了。
提升近似精度:⼆元函数的泰勒多项式
同样地,⽤⼀个切平⾯去近似⼀个曲⾯,误差肯定在所难免,而且是不小的,那该怎么办呢?
回忆我们之前讲过的,⽤切线去近似⼀元函数特定点邻域内的函数值的表达式:
\[p_1(x) = f(x_0) + f'(x_0)(x - x_0)\]它实际上是⼀元函数的⼀阶泰勒展开式,为了提⾼近似精度,我们使⽤更⾼阶的 n 阶泰勒展开式。
那么同样的,在⼆元函数 f(x,y) 中,使⽤切平⾯去近似$(x_0, y_0)$邻域内的函数值,即:
\[P_1(x, y) = f(x_0, y_0) + [f_x(x_0, y_0)(x - x_0) + f_y(x_0, y_0)(y - y_0)]\]这也是⼆元函数的⼀阶泰勒多项式。
为了提⾼它的精度,我们同样可以使⽤阶数更⾼的⼆元函数泰勒多项式,当然限于篇幅和复杂性,我们这⾥只举⼆元函数的 ⼆阶泰勒多项式,让⼤家有⼀个直观的认识:
\[P_2(x, y) = f(x_0, y_0) + [f_x(x_0, y_0)(x - x_0) + f_y(x_0, y_0)(y - y_0)] + \frac{1}{2}[f_{xx}(x_0, y_0)(x - x_0)^2 + 2f_{xy}(x_0, y_0)(x - x_0)(y - y_0) + f_{yy}(x_0, y_0)()y - y_0]^2\]我们写成矩阵相乘的形式,会看得更加清晰⼀些:
\[f(x, y) \approx f(x_0, y_0) + \begin{bmatrix}\frac{\partial f}{\partial x}(a, b) & \frac{\partial f}{\partial y}(x_0, y_0)\end{bmatrix}\begin{bmatrix}x - x_0 \\ y - y_0\end{bmatrix} + \frac{1}{2} \begin{bmatrix}x - x_0 & y - y_0\end{bmatrix}\begin{bmatrix}\frac{\partial^2 f}{\partial x^2}(x_0, y_0) & \frac{\partial^2 f}{\partial x \partial y}(x_0, y_0) \\ \frac{\partial f^2}{\partial y \partial x}(x_0, y_0) & \frac{\partial^2 f}{\partial y^2}(x_0, y_0)\end{bmatrix}\begin{bmatrix}x - x_0 \\ y - y_0\end{bmatrix}\]实际举例
我们来实际举个例⼦:
\[z = f(x, y) = 1 - e^{-x^2 - 2y^2}\] \[p_1(x, y) = 0\] \[p_2(x, y) = x^2 + 2y^2\]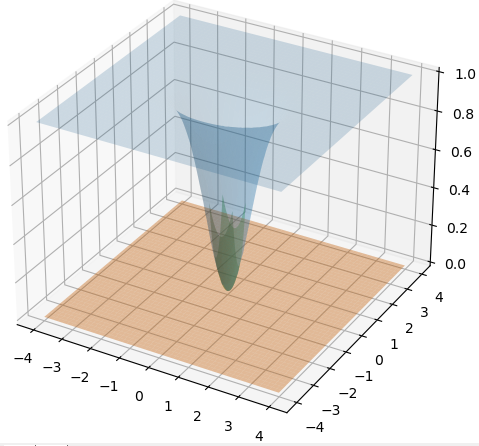
我们看到,原函数的图像是蓝⾊的,我们在 (0,0) 点附近对函数的取值进⾏近似处理,橙⾊的切平⾯是原函数的⼀阶泰勒近似,看上去它的误差⾮常⼤。而绿⾊的曲⾯是原函 数的⼆阶泰勒近似,近似的精度就提升了很多。
偏导数的链式法则
如果 x 和 y 是关于 s 和 t 的函数,也就是说 x=x(s,t),y=y(s,t),并且变量 x 和 y 关于 s 和 t 的一阶偏导数都存在,那么满足可微性的二元函数 z=f(x,y) 关于变量 s 和 t 的偏导数就可以利用如下的链式法则求出:
\(\frac{\partial z}{\partial s}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial s}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial s}\) \(\frac{\partial z}{\partial t}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial t}\)
看上去略显复杂,我们举个小例子:
\[z=4x^2-2y^2,x=s+7t,y=4st\]那么 $\frac{\partial z}{\partial t}$ 的求解过程如下:
$\frac{\partial z}{\partial t}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial t}$ $=8x\cdot 7+(-4y)(4s)$ $=56(s+7t)-16s4st$ $=56s+392t-64s^2t$