通过梯度场直观感受梯度
⼆元函数中的梯度概念可以说是⼀元函数中导数概念的⼀个延伸和拓展。
它们之间的区别是⼀元函数的导数 f’(x) 是⼀个数,而梯度$\nabla f(p)$则是⼀个向量,对于⼆元函数 f(x,y),梯度对应的向量就是$(f_x, f_y)$ ,向量的概念⼤家都很熟悉,它是⼀个有⽅向、有⼤小的量。
对于⼀个⼆元函数 f(x,y),在它的定义域内,如果我们把每⼀个点的梯度都求出来,将每个点的梯度向量和各个点的位置联系起来进⾏集中展 ⽰,就形成了⼀个梯度场,场的概念是⼀个⽐较新的概念,我们还是针对⼆元函数$f(x, y) = x^2 - y^2$来实际展⽰⼀下。
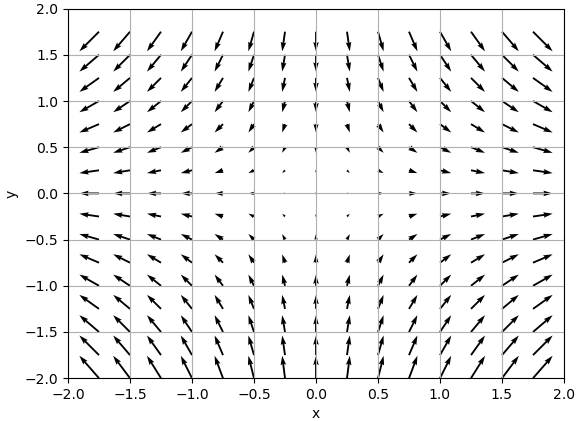
在 x 坐标轴上,从 -2 到 2,按照 0.25 的间隔,我们⼀共⽣成了 16 个点,y 坐标也是同理,⼀共也是有 16 个点,这样就对应表⽰出了平⾯上的 256 个点。
通过:
1
X,Y=np.meshgrid(x,y)
进⾏⽹格化,得到的 X 是⼀个⼆维数组,16 ⾏ 16 列,对应表⽰平⾯上的 256 个点的横坐标,同样 Y 也是⼀个⼆维数组,16 ⾏ 16 列依次对应,表⽰上⾯那 256 个点的纵坐标。
1
2
X=X.flatten()
Y=Y.flatten()
上⾯的这两⾏代码将这两个⼆维数组展平成⼀维数组,X 和 Y 都变成含有 256 个元素的⼀维数组,其中 X[i] 和 Y[i] 分别对 应表⽰这 256 个点中第 i 个点的横纵坐标。
1
2
3
4
5
6
def numerical_gradient(f,P):
grad=np.zeros_like(P)
for i in range(P[0].size):
grad[0][i]=grad_x(f,P[0][i],P[1][i])
grad[1][i]=grad_y(f,P[0][i],P[1][i])
return grad
上面numerical_gradient这个函数, ⽤于求取整个定义域上的梯度,传⼊的 P 是⼀个$2 \times 256$的数组,P[0] 就是所有点的 x 坐标构成的⼀维数组 X,而 P[1] 就是所有点的 y 坐标构成的⼆维数组 Y,我们利⽤数值求解 的⽅法求取各个点的偏导数$f_x$和$f_y$ ,同样存储在⼀个$2 \times 256$的⼆维数组$grad$当中,其中$grad[0][i]$和$grad[1][i]$分别代表了第 i 个点的$f_x$和$f_y$ ,因此向量$(grad[0][i], grad[1][i])$所表⽰的就是第 i 个点的梯度。
最后我们利⽤$plt.quiver(X, Y, grad[0], grad[1])$将所有点的梯度⽤箭头的形式绘制出来,X,Y 表⽰箭头的起点,$grad[0]$ , $grad[1]$表⽰的是箭头的⽅向。
任意方向上的方向导数
对于⼀个⼆元函数 f(x,y) 而⾔,偏导数$f_x$的⼏何意义是表⽰沿着平⾏于 x 轴⽅向上的函数值的变化率,相应的偏导数$f_y$则表⽰的是沿着平⾏于 y 轴⽅向上的函数值的变化率。
我们⽤向量来表⽰这个求导的过程,就会更加清晰地展现其⼏何意义。
我们⽤向量 p 表⽰所求偏导的对应点 (x,y),即 p=(x,y),⼀般我们⽤ i 和 j 分别表⽰平⾏于 x 轴和 y 轴的单位向量,那么我们可以分别重新⽤向量来表⽰偏导数$f_x$和$f_y$。
$f_x(p) = \lim_{h \rightarrow 0} \frac{f(p + hi) - f(p)}{h}$, 我们将其记作: $D_i f(p)$。
$f_y(p) = \lim_{h \rightarrow 0} \frac{f(p + hj) - f(p)}{h}$, 我们将其记作: $D_j f(p)$
我们⽤向量来表⽰出了沿着 x 轴⽅向的偏导数$f_x$以及沿着 y 轴⽅向的偏导数$f_y$,但这只是反映了函数沿特殊⽅向上的变化率。那么我们最终来看⼀般化的情况,如何表⽰沿着任意⽅向的⽅向导数?
我们设对于任意⽅向上的单位向量 u,依照定义,⼆元函数 f(p) 在 p 处沿着⽅向 u 的⽅向导数为:
\[D_u f(p) = \lim_{h \rightarrow 0} \frac{f(p + hu) - f(p)}{h}\]当然前提条件是这个极限得存在。它反映了函数值沿着⽅向向量 u 的变化率。
方向导数和梯度的关系
实际上,根据前⾯所讲过的内容,⼆元函数 f(x,y) 如果在点 p 处可微,那么⼀定满⾜如下的式⼦:
\[f(p + hu) - f(p) = \nabla f(p) · (hu) + \epsilon(hu) · (hu)\]向量$(f_x(p_0), f_y(p_0))$称之为函数$f$在$p_0$处的梯度 ,有专⻔的记号,我们记作为:$\nabla f(p_0)$ 。
h为增量$h = (h_1, h_2)$, u是任意方向上的单位向量。
那么, 当$h \rightarrow 0$时, $\epsilon(hu) \rightarrow 0$, 那么一定满足如下的式子:
\[\lim_{h \rightarrow 0} \frac{f(p + hu) - f(p)}{h} = \nabla f(p)·u\]而此时,我们仔细⼀看,这个表达式的左侧$\lim_{h \rightarrow 0}\frac{f(p+hu) - f(p)}{h}$正是函数 f 在 p 点处沿着⽅向向量 u 的⽅向导数$D_u f(p)$ ,因此我们得到了我们想要看到的⼀个结论:
\[D_u f(p) = \nabla f(p) · u\]它说明了函数 f 在点 p 处沿⽅向向量 u 的⽅向导数(也就是函数值的变化率)$D_u f(p)$ ,等于该点处的梯度向量与⽅向向量 u 的点积。
最⼤变化率、梯度与等位线
梯度与最⼤变化率的关系
\[D_u f(p) = \nabla f(p) · u\]我们把点积的式⼦进⼀步展开后得到:
\[D_u f(p) = \nabla f(p) · u = \mid f(p) \mid \mid u \mid cos \theta\]其中$\theta$是梯度向量$\nabla f(p)$和⽅向向量 u 的夹⻆,那么如果我们想知道在哪个⽅向上的 f 的函数值变化最快,该怎么去分析?
由于$-1 \leq cos \theta \leq 1$,显然
\[- \mid \nabla f(p) \mid \mid u \mid \leq D_u f(p) \leq \mid \nabla f(p)\mid \mid u \mid\]也就是说,当$\theta = 0$,即⽅向向量 u 和梯度向量$\nabla f(p)$同向时,变化率的取值最⼤,即增⻓得最快,为$\mid \nabla f(p)\mid \mid u \mid$ ,由于 u 是单位向量,因此变化速率为$\mid \nabla f(p)\mid$ 。
当 ,即⽅向向量 u 和梯度向量$\nabla f(p)$反向时,变化率的取值最小,即下降得最快,变化率为$-\mid \nabla f(p)\mid \mid u \mid$。
总结起来就是在 p 点的函数值沿着梯度的⽅向增加得最快,逆着梯度的⽅向函数值减小得最快。
梯度与等位线的关系
我们知道,同⼀等位线上的函数值都是相等的,因此 p 点处等位线切线⽅向(我们令单位向量 u 沿着等位线的切线⽅向)上函数值的变化率$D_u f(p)$显然应该为 0,那么就有:
\[0 = D_u f(p) = \nabla f(p)·u\]即:点 p 处的梯度向量和过 p 点的等位线的切线⽅向向量 u 的点积为 0,这就说明函数 f 在点 p 处的梯度和经过该点的等位 线是相互垂直的。
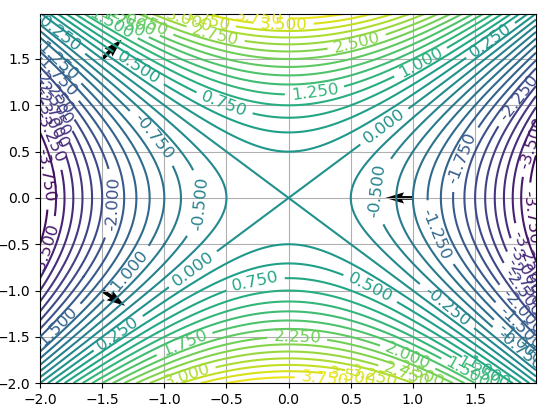
我们实际观察⼀下,我们绘制函数$f(x, y) = y^2 - x^2$的等位线,然后随机在定义域内选取三个点 (-1.5,1.5)、(-1.5,-1)、(1.0,0),并绘制其梯度向量,观察是否满⾜和对应点处等位线的垂直关系。