概率图的最基本含义
概率图,从字⾯上理解就是“概率”+“图”,“概率”指的就是概率模型,把概率引⼊到机器学习的世界⾥是⼀件⾮常⾃然的事情,这样我们就能够实现对已有的数据进⾏聚类 (例如混合⾼斯模型),或者对未知的数据进⾏预判(例如朴素⻉叶斯、逻辑回归等),这是机器学习的核⼼思想。
“图”和我们在数据结构中学习过的图是⼀个意思,它包含了有向图、⽆向图。
对上述的图结构赋予概率的内涵,即将概率嵌⼊到图结构当中,形成概率图模型。这么⼲,⼀⽅⾯会使得表达上更为清晰直 观,另⼀⽅⾯可以⽤图结构把概率的特征体现的更加明显,以便于我们去构造⼀些更加⾼级的模型。
经常处理的概率和运算法则
⽤来描述样本的数据往往是多维的,因此在现实中⼀般都是⽤⾼维、多元的随机变量来表⽰数据。例如⼀个$p$维的随机变量$(x_1, x_2, …, x_p)$,我们⼀般会关注⼏种概率分布的形式:
- 联合概率:$p(x_1, x_2, …, x_p)$
- 边缘概率:$p(x_i)$
- 条件概率:$p(x_i \mid x_j)$
此时我们再回顾⼀下围绕着这三个概率的运算符法则
和准则:
\[p(x_1) = \int p(x_1, x_2)dx_2\]积准则
\[p(x_1, x_2) = p(x_1)p(x_2 \mid x_1) = p(x_2)p(x_1 \mid x_2)\]链式法则:
\[p(x_1, x_2, ..., x_p) = p(x_1)p(x_2 \mid x_1)p(x_3 \mid x_2, x_1) ... p(x_p \mid x_{p-1}x_{p-2}...x_1)\]贝叶斯法则:
\[p(x_2 \mid x_1) = \frac{p(x_1, x_2)}{p(x_1)} = \frac{p(x_1, x_2)}{\int p(x_1, x_2)dx_2} = \frac{p(x_2)p(x_1 \mid x_2)}{\int p(x_2)p(x_1 \mid x_2)dx_2}\]高维随机变量的困境与解决探索
随机变量的维度⾼了,⾃然而然的就使得联合概率 的计算⾮常复杂。
那么⾯对复杂,⼈们⾃然而然的就想着去简化模型,简化的⽅法,就是施加某些前提假设,来化解这其中的复杂性。
⾸先要提的就是朴素⻉叶斯模型,在描述以类别为条件的概率$p(x_1, x_2, …, x_p \mid y)$中,它假设给定类别 的情况下,⾼维随机变量中各个维度是彼此独⽴的,在这个前提下,概率就⾮常容易的得到了分解:
\[p(x \mid y) = p(x_1, x_2, ..., x_p \mid y) = \prod_{i=1}^p p(x_i \mid y)\]朴素⻉叶斯简便归简便,但是问题在于它的假设过强了,实际中,⾼维随机变量的各个维度之间有极⼤的可能性是互相不独⽴的,因此这个$x_i \perp x_j \mid y$前提假设就不存在,也就不能按照这个⽅式进⾏分解了。
我们进⼀步的放松这个前提假设,就不得不提在随机过程中介绍过的⻬次⻢尔科夫模型(我们以⼀阶为例):

在这个我们熟悉的⼀阶⻢尔科夫模型中,我们知道, $x_3$的状态仅与$x_2$相关,而与$x_1$⽆关, $x_4$的状态仅与$x_3$有关,而与之前的$x_1$、$x_2$均⽆关,即⽤表达式$x_j \perp x_{i+1} \mid x_i, j<i$来表⽰,通过这种⽅式也达到了简化联合概率表⽰形式的⽬的:
\[\begin{aligned} p(x_1, x_2, ..., x_p) &= p(x_1)p(x_2 \mid x_1)p(x_3 \mid x_2, x_1)...p(x_p \mid x_{p-1}x_{p-2}x_{p-3}...x_1) \\ & = p(x_1)p(x_2 \mid x_1)p(x_3 \mid x_2) ... p(x_p \mid x_{p-1}) \end{aligned}\]联合概率的表达形式也得到了简化,但是话说回来,⼀阶⻢尔科夫性的假设实际上也过强了,因为它把各个维度之间的依赖 和关联关系限定的过于简单和单⼀,实际上许多的依赖关系绝不仅仅限于此,⽐如下⾯这种:
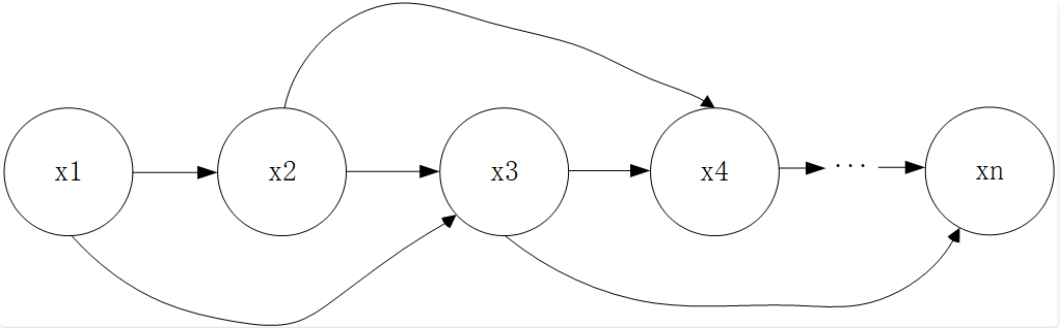
我们随意在⼏个维度之间增加了依赖关联关系,⻢尔科夫性就⽆法描述这种情形了。
因此我们还需要进⼀步的去探索更为泛化的⽅法来化解⾼维随机变量的复杂性,这是概率图模型的⼀个⾮常核⼼并且⾮常⾸ 要的问题,有了合适的⽅法,我们就能⼀⽅⾯利⽤概率图来直观地表⽰⾼维随机变量,另⼀⽅⾯⼜能够很好地化解它的复杂性。
概率图中的几个主要研究目标
概率图模型中有三⼤基本问题:表⽰(representation)、推断(inference)和学习(learning)。
数据结构中,图分为有向图和⽆向图,那么概率图同样也就分为了有向图和⽆向图,其中有向图称为是⻉叶斯⽹络,而⽆向 图称为是⻢尔科夫⽹络(或者称之为⻢尔科夫随机场),这就是概率图的表⽰。
推断问题的本质就是根据已知的数据,去求另外⼀些数据的概率分布,有精确推断,以及在⼯程中使⽤更⼴的近似推断。
学习问题就更好理解了,主要是学两块内容,⼀块是参数学习,另⼀块是结构学习。