距离空间
在高等数学中:
- 研究对象——函数
- 基本工具——极限, 是分析理论的基础
- 定义极限的基础——距离
在泛函分析中将上述内容推广
- 研究对象——算子、泛函(空间到空间的映射)
- 首先引入度量工具——距离
- 然后在度量空间中——定义极限, 建立相应的理论
- 进一步对每一个具体空间引入相应的结论
距离空间
设$X$是非空集合, 若$\forall x, y \in X \rightarrow \exists \mid \rho (x, y) \geq 0$, 且满足
- 非负性 $\rho(x, y) \geq 0$, 当且仅当$x = y$时, $\rho(x, y) = 0$
- 对称性 $\rho(x, y) = \rho(y, x)$
- 三角不等式: $\forall x, y, z \in X$, 有$\rho(x, y) \leq \rho(x, z) + \rho(z, y)$
则称实数$\rho(x, y)$为元素$x$与$y$之间的距离, 称$X$为距离空间或度量空间, 记作$(X, \rho)$或$X$。 距离空间中的元素也称为“点”, 用“·”表示。
距离$\rho(·, ·)$是集合$X \times X$(称为乘积空间或笛卡尔积空间)到实数集合$R^1$上的二元泛函(或称函数)。
设$R^n$是$n$维向量全体构成的空间
$\forall x = (x_1, x_2, …, x_n)^T, y = (y_1, y_2, …, y_n)^T \in R^n$
定义$\rho(x, y) = \sqrt{\sum_{i=1}^n (x_i - y_i)^2}$
$R^n$在$\rho$下为距离空间, 即通常意义下的欧式空间。
特别的, 当$n=1$时, $\rho(x, y) = \mid x - y \mid$ 当$n=2$时, $\rho(x, y) = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2}$
如果在$R^2$中, 定义$d(x, y) = \mid x_1 - y_1 \mid + \mid x_2 - y_2 \mid$, 验证得知$R^2$按$d$也是距离空间,但与欧式空间是不同的度量空间。
向量范数
若$n$维向量$x = (x_1, x_2, …, x_n)^T \in R^n$对应的某个非负实数$N(x) = |x|$满足条件
- 正定性: $| x | \geq 0$, 且$|x| = 0 \Leftrightarrow x= 0$;
- 正齐性: 对任意实数$\alpha$, 都有$|\alpha x| = \mid \alpha \mid |x|$;
- 三角不等式: 对任意$x, y \in R^n$, 有$|x + y | \leq |x| + |y|$
则称$| x |$是$R^n$上的一个向量范数。
常用的向量范数:
- $\infty - 范数$: $| x |{\infty} = \max{1 \leq i \leq n} \mid x_i \mid$
- 1-范数: $|x|1 = \sum{i=1}^n \mid x_i \mid$
- 2-范数或欧式范数: $|x|2 = (\sum{i=1}^n x_i^2)^\frac{1}{2}$
利用范数$|x - y |$可度量向量$x$与$y$的误差。
定理1(范数的连续性): 设$x$是$R^n$上任一种向量范数, 则$|x|$是向量$x$的分量$(x_1, x_2, …, x_n)$的连续函数。
定理2(向量范数的等价性): 设$|·|_s$和$|·|_t$是$R^n$上任意两种范数, 则存在常数$C_1, C_2 > 0$, 使:
\[C_1\|x\|_s \leq \|x\|_t \leq C_2 \|x\|_s, \forall x \in R^n\]由定理2可得: $R^n$上任意两种向量范数等价
定理3: $\lim_{k \rightarrow \infty} x^{(k)} = x^*$的充分必要条件是对任意一种范数,
\[\|x^{(k)} - x^*\| \rightarrow 0\]矩阵范数
设$n$阶方针$A = (a_{ij})_{n \times n} \in R^{n \times n}$, 若对应一个非负实数$| A |$, 满足下列条件:
- 正定性: $|A| \geq 0$, 且$|A| = 0 \Leftrightarrow A = 0$
- 正次性:对任意实数$\lambda$, $| \lambda A| = \mid \lambda \mid | A |$
- 三角不等式: $\forall A, B \in R^{n \times n}$, 有$| A + B | \leq |A| + |B|$
- 乘积不等式: $\forall A, B \in R^{n \times n}$, 有$| A B | \leq |A||B|$
则称$|A|$为$n$阶矩阵$A$的范数。
定义$A \in (a_{ij})_{n \times n}$的一种范数
\[\|A\|_F = (\sum_{i=1}^n \sum_{j=1}^n \mid a_{ij}\mid^2)^{\frac{1}{2}}\]斐波那契范数(Froubenius),称为矩阵A的F-范数。可以看成是$n \times n$维向量的2-范数。
定义: 如果$\forall A \in R^{n \times n}$及$\forall x \in R^n$, 都有
\[\| Ax \| \leq \|A\|\|x\|\]成立, 则称矩阵范数$|A|$与向量范数$|x|$是相容的。
定义(矩阵的算子范数): 设$x \in R^n, A \in R^{n \times n}$, 给出一种向量范数$|x|v$, 例如$v = 1, 2, \infty$, 相应地定义一个矩阵的非负函数$|A|_v = \max{x \neq 0} \frac{|Ax|_v}{|x|_v}$, 其满足矩阵范数的条件, 称为矩阵的算子范数。
ps:
- 矩阵的算子范数也称为由向量范数诱导出的范数。
- 矩阵的算子范数与向量范数具有相容性。
三种常用的矩阵的算子范数公式
定理4:设$x \in R^n, A \in R^{n \times n}$, 则:
- $|A|{\infty} = \max{x \neq 0} \frac{|Ax|{\infty}}{|x|{\infty}} = \max_{i \leq i \leq n} \sum_{j=1}^n \mid a_{ij} \mid$ , A的行范数
- $|A|{1} = \max{x \neq 0} \frac{|Ax|{1}}{|x|{1}} = \max_{i \leq j \leq n} \sum_{i=1}^n \mid a_{ij} \mid$ , A的列范数
- $|A|2 = \sqrt{\lambda{max}(A^TA)}$, A的2范数($\lambda_{max}$是最大特征值)。
三种矩阵范数等价
定义(谱半径): 设$A \in R^{n \times n}$的特征值为$\lambda_i(i = 1~n)$, 称
\[\rho(A) = \max_{1 \leq i \leq n} \mid \lambda_i \mid\]为矩阵A的谱半径。
定理5: 设$A \in R^{n \times n}$, 则$\rho(A) \leq |A|$。
定理5说明矩阵A的谱半径不超过A的任意一种算子范数。
定理6:如果$A \in R^{n \times n}$为对称矩阵, 则$\rho(A) = |A|_2$。
证明:设$\lambda_i$是A的任意特征值, $u_i$为对应特征向量
$\because$ $A^T = A$
$\therefore A^T A u_i = AAu_i = A \lambda_i u_i = \lambda_i A u_i = \lambda_i^2 u_i$
$|A|^22 = \lambda{max}(A^TA) = max_{1 \leq i \leq n} \lambda_i^2 = (\max_{1 \leq i \leq n} \mid \lambda_i \mid)^2 = (\rho(A))^2$
$\Rightarrow |A|_2 = \rho(A)$
定理7: 如果$|B| < 1$, 则$I \pm B$为非奇异矩阵, 且:
\[\|(I \pm B)^{-1}\| \leq \frac{1}{1 - \|B\|}\]注: 这里$|·|$指矩阵的算子范数。
赋范线性空间
线性空间
设$E$是非空集合,$K$是实数(或复数)域。 在$E$中定义两种运算:
- 加法: $\forall x, y \in E$,存在唯一$z \in E$, 记作$z = x + y$
- 数乘: $\forall x \in E, \lambda \in K$, 存在唯一$\delta \in E$, 记作$\delta = \lambda x$
且满足下列八条运算规律:
$E \times E \rightarrow E \qquad “+”$
- $x + y = y + x$
- $(x + y) + z = x + (y + z)$
- $\exists “零元素” \theta \in E$, 有$x + \theta = x$
- $\exists “负元素” -x \in E$, 有$x + (-x) = \theta$
$K \times E \rightarrow E \qquad “·”$
- $\lambda(\mu x) = (\lambda \mu)x$
- $1 · x = x, 0 · x = \theta$
- $(\lambda + \mu)x = \lambda x + \mu x$
- $\lambda(x + y) = \lambda x + \lambda y$
称$E$是(数域$K$上的)线性空间(或向量空间)。 满足八条规律的两种运算称为线性运算。
例子:
$P_n(x)$——次数不超过$n$的多项式全体, 在通常的“加法”“数乘”运算下 是 线性空间。
$Q_n(x)$——次数等于$n$的多项式全体, 在通常意义“加法”“数乘”运算下 不是 线性空间。
- $C[a, b]$表示定义在$[a, b]$上的所有连续函数的全体
- $L^2[a, b] = (x(t) \mid \int_a^b \mid x(t) \mid^2 dt < + \infty$表示定义在$[a, b]$上的平方可积函数。
$C[a,b]、 L^2[a, b]$在通常意义下的“加法”“数乘”运算下 是 线性空间。
赋范线性空间
设$E$是实数域(或复数域)K上的线性空间。若$\forall x \in E \rightarrow \exists 实数 |x| \geq 0$, 且满足下列三个条件:
- 正定性: $|x| \geq 0$, 当且仅当$x = 0$时, $|x| = 0$
- 正次性: $|\alpha x| = \mid \alpha \mid · |x|$
- 三角不等式: $\forall x, y \in E$, 有$|x + y| \leq |x| + |y|$
则称实数$|x|$为$x$的范数, 称$E$为赋范线性空间, 记作$(E, |·|)$或$E$。
即在线性空间中定义了 范数的空间, 称为 赋范线性空间。
例1:
在欧式空间$R^n$中,
\[\forall x = (x_1, x_2, ..., x_n), y = (y_1, y_2, ..., y_n) \in R^n\]定义:
- $|x|2 = \sqrt{\sum{i=1}^n x_i^2}$, 则$(R^n, |x|2)$是赋范线性空间。定义距离$d(x, y) = |x - y|_2 = \sqrt{\sum{i=1}^n (x_i - y_i)^2}$
- $|x|\infty = \max{1 \leq i \leq n} \mid x_i \mid$, 则$(R^n, |x|_{\infty})$是赋范线性空间。
- $|x|1 = \sum{i=1}^n \mid x_i \mid$, 则$(R^n, |x|_1)$是赋范线性空间。
例2:
$C[a, b]$是线性空间, 若定义
- $|x| = \max_{t \in [a, b]}\mid x(t) \mid$, 则$(C[a, b], |x|)$是赋范线性空间。定义距离$d(x, y) = |x - y| = \max_{t \in [a, b]} \mid x(t) - y(t) \mid$。
- $|x|_1 = \int_a^b \mid x(t) \mid dt$, 则$(C[a, b], |x|_1)$是赋范线性空间。
例3:
$L^2[a, b]$是线性空间, 若定义
\[\|x\| = (\int_a^b \mid x(t)\mid^2 dt)^{\frac{1}{2}}\]则$(L^2[a, b], |x|)$是赋范线性空间。
定义距离$d(x, y) = |x - y| = (\int_a^b \mid x(t) - y(t)\mid dt)^{\frac{1}{2}}$
赋范线性空间中的点列及性质
定义1(收敛点列)
设${x_n}$是赋范空间$E$中的一个点列, 若:
\[\|x_n - x\| \rightarrow 0, n \rightarrow \infty\]则称${x_n}$为收敛点列, 记作$\lim_{n \rightarrow \infty} x_n = x$。
定义2(柯西点列)
设${x_n}$是赋范空间$E$中的一个点列,若:
\[\|x_{n+p} - x_n\| \rightarrow 0, n \rightarrow \infty, \forall p \in Z^+\]则称点列${x_n}$为 Cauchy点列 或 基本点列。
例1:
在$R^1$中, 地哦按咧${x_n} = {\frac{1}{n}}$, 是收敛点列, 也是Cauchy点列。
PS: $R^1$中有结论: ${x_n}$是收敛数列 $\Leftrightarrow$ ${x_n}$是Cauchy数列。 但在一般的距离空间中,该结论不成立。
例2:
在有理数空间$Q$中, 点列
\[1, 1.4, 1.41, 1.414, 1.4142, ... \rightarrow \sqrt{2} \notin Q\]是$Q$中的Cauchy点列, 但不是收敛点列;
同理, 点列${x_n} = {(1 + \frac{1}{n})^n}$是$Q$中Cauchy点列, 但不是收敛点列。
性质1(极限唯一性): 在赋范空间$E$中的收敛点列$x_n$的极限点是唯一的。
性质2(极限存在的有界性): 在赋范空间$E$中的收敛点列$x_n$必有界。
性质3(范数的连续性): 在赋范空间$E$中, $|x - y|$是两个变元$x, y$的连续泛函。 即当$x_n \rightarrow x_0, y_n \rightarrow y_0$时:
\[\|x_n - y_n \| \rightarrow \|x_0 - y_0 \|(n \rightarrow \infty)\]性质4: 若${x_n}$是$(E, |·|)$中的收敛点列, 则${x_n}$一定是Cauchy点列; 反之, Cauchy点列不一定是收敛点列
定义(完备性): $X$是赋范线性空间, 若$X$中的任一Cauchy点列都在$X$中收敛, 则称$X$是完备的赋范线性空间。
结论: 在完备的赋范空间中,收敛点列与Cauchy点列是等价的。
内积空间
内积空间
设$U$是数域$K$(实或复数域)上的线性空间, 若$\forall x, y \in U$, 存在唯一的数$(x, y) \in K$, 满足下列条件:
- 正定性: $(x, x) \geq 0$, $(x, x) = 0 \Leftrightarrow x = 0$
- 共轭对称性: $(x, y) = \overline{(y, x)}$
- 关于第一变元的线性性质:$(\alpha x + \beta y, z) = \alpha(x, z) + \beta(y, z), z \in U$
则称$(x, y)$为$x, y$的内积, $U$为内积空间。
注: 内积$(·, ·)$是$U \times U \rightarrow R$(或$C$)的二元泛函。
当$K$是实数域时, 称$U$为实内积空间; $K$为复数域时, 称$U$为复内积空间。 通常$U$指的是复内积空间。
内积关于第二变元满足共轭线性性质
\[(x, ay) = \overline{(\alpha y, x)} = \overline{\alpha} \overline{(y, x)} = \overline{\alpha}(x, y)\] \[(x, y + z) = \overline{(y + z, x)} = \overline{(y, x)} + \overline{(z, x)} = (x, y) + (x, z)\]故:
\[(x, \alpha y + \beta z) = \overline{\alpha} (x, y) + \overline{\beta}(x, z)\] \[(\alpha x + \beta y, z) = \alpha(x, z) + \beta (y, z), z \in U\]例1:
在实向量空间$R^n$中
\[\forall x = (x_1, ..., x_n)^T, y = (y_1, ..., y_n)^T \in R^n\]定义内积: $(x, y) = \sum_{i=1}^n x_i y_i$
而在复向量空间$C^n$中, $\forall x, y \in C^n$
定义内积: $(x, y) = \sum_{i=1}^n x_i \bar y_i$
例2:
在平方可积函数空间$L^2[a, b]$中, $\forall x(t), y(t) \in L^2[a, b]$,
定义内积: $(x, y) = \int_a^b x(t) · \overline{y(t)} dt$
若$L^2[a, b]$位平方可积实值函数空间, 则:
定义内积: $(x, y) = \int_a^b x(t) · y(t) dt$
例3
在$C[a,b]$, 定义内积:
\[(x, y) = \max_{t \in [a, b]} \mid x(t) - y(t) \mid\]内积空间的性质
性质1: 内积满足Cauchy-Schwarz(柯西——许瓦兹)不等式
\[\mid (x, y) \mid \leq \sqrt{(x, x)} · \sqrt{(y, y)}\]性质2: 内积可诱导范数
在内积空间$U$中,由内积定义$|x| = \sqrt{(x, x)}$, 验证知满足范数的三条公理。 因此,内积空间一定是赋范线性空间。
$(x,x)$表示内积, 比如定义$\int_a^b f(t) \overline{g(t)}dt$, 其诱导的范数为$\sqrt{\int_a^b\mid x(t) \mid^2}dt$。诱导的距离是$|x-y|$, 即$x-y$的范数, 这里的范数指的就是内积诱导出的范数, $|x - y| = \sqrt{\int_a^b \mid x(t) - y(t) \mid^2 dt}$
例1:
在实向量空间$R^n$中, 由内积$(x, y) = \sum_{i=1}^n x_i y_i$诱导的范数:
\[\| x \| = \sqrt{(x, x)} = \sqrt{\sum_{i=1}^n x_i^2}\]在平方可积函数空间$L^2[a, b]$中, 由内积$(x, y) = \int_a^b x(t)· \overline{y(t)}dt$诱导的范数:
\[\|x\| = \sqrt{\int_a^b \mid x(t) \mid^2 dt}\]因此内积空间$R^n$, $L^2[a, b]$也是赋范线性空间。
性质3: 在内积空间$U$中, 按内积导出的范数满足平行四边形公式:
\[\|x + y\|^2 + \|x - y\|^2 = 2(\|x\|^2 + \|y\|^2)\]证明:
\[\begin{aligned} \|x + y\|^2 + \|x - y\|^2 & = (x+y, x+y) + (x-y, x-y) \\ & = \|x\|^2 + (x, y) + (y, x) + \|y\|^2 + \|x\|^2 - (x, y) - (y, x) + \|y\|^2 \\ & = 2(\|x\|^2 + \|y\|^2) \end{aligned}\]性质4: 在内积空间$U$中, 内积$(x, y)$是两个变元$x, y$的连续泛函。
即$x_n \rightarrow x, y_n \rightarrow y$(按范数)时, 数列$(x_n, y_n) \rightarrow (x, y)$。
Hilbert空间
完备的内积空间$U$称为Hilbert空间, 记作$H$(即内积空间$U$按范数$|x| = \sqrt{(x, x)}$成为Banach空间)。
例:
$R^n$在内积定义$(x, y) = \sum_{i=1}^n x_i y_i$下, 是Hilbert空间。
$L^2[a, b]$在内积定义$(x, y) = \int_{a}^b x(t) · \overline{y(t)}dt$下, 是Hillbert空间。
$C[a, b]$在内积定义$(x, y) = \max_{t \in [a, b]} \mid x(t) - y(t) \mid$下, 是Hillbert空间。
正交分解和投影定理
定义
设$U$是内积空间, 元素$x, y \in U$, 集合$M, N \subset U$
- 若$(x, y)=0$, 称$x$与$y$正交, 记作$x \perp y$
- 若$\forall y \in M$, 有$(x, y) = 0$, 称$x$与$M$正交, 记作$x \perp M$
- 若$\forall x \in M, \forall y \in N$, 有$(x, y) = 0$, 称$M$与$N$正交, 记作$M \perp N$
- $U$中与$M$正交的所有元素的全体称为$M$的正交补, 记作$M^{\perp}$, 即: \(M_{\perp} = \{y \mid y \perp x, x \in M\}\)
- 设$M$为$U$的线性子空间, $x \in U$, 若$\exists x_0 \in M, x_1 \in M^{\perp}$, 使得 \(x = x_0 + x_1 \tag{*}\) 则称$x_0$为$x$在$M$上的正交投影, $(*)$式称为对$x$的正交分解。
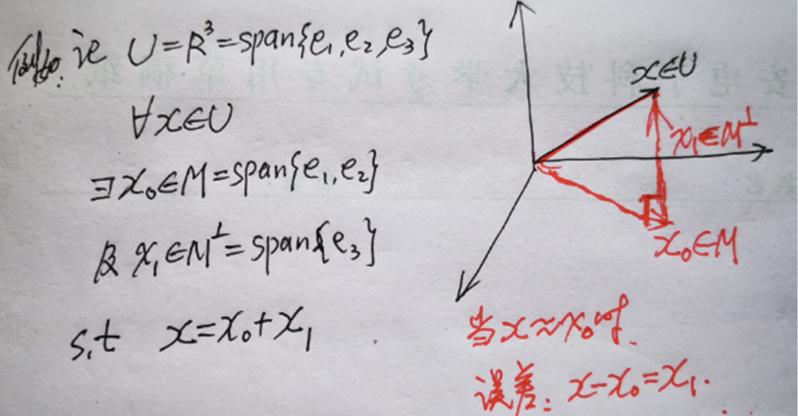
正交分解的性质
1) 设$U$是内积空间, $x, y \in U$, 若$x \perp y$, 则
\[\|x + y\|^2 = \|x\|^2 + \|y\|^2\]称为内积空间中的“商高定理”。
2)设$U$是内积空间, $M \subset U$, 则$M^{\perp}$必为$U$中闭的线性子空间。
3)设$M$是$U$中闭的线性子空间, 则正交投影是存在唯一的, 即$\forall x \in U$,$\exists 1 x_0 \in M, x_1 \in M^{\perp}$, 使得:
\[x = x_0 + x_1, \qquad \text{且}\|x - x_0\| = \min_{y \in M} \|x - y\|\]称$x_0$是$x$在$M$中的最佳逼近元。
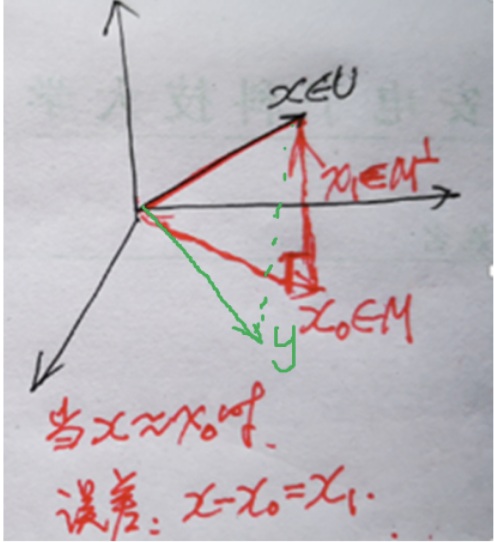
性质3)表明: $x$在$M$中的最佳逼近元就是$x$在$M$中的投影, 因此, 在内积空间中的最佳逼近元问题就是正交投影问题。
投影定理
设$M$是$Hillbert$空间$H$的闭线性子空间, 则$\forall x \in H$及$x_1 \in M^{\perp}$, 使得:
\[x = x_0 + x_1\]推广: 若$M$是内积空间$U$的完备子空间, 定理结论仍成立。
PS: 任何有限维赋范线性空间一定是完备的。