有向图对概率模型的表达
概率图模型将抽象的图赋予了概率的含义,而概率图模型的中⼼问题就是多维 随机变量的联合概率分布$p(x_1, x_2, …, x_p)$的计算, 而⾼维度就是导致链式法则计算的直接原因,由此我们想了很多办法去进⾏简化。
我们就基于有向概率图模型来谈谈如何进⾏联合概率表达式的简化,以及其中的窍⻔:条件独⽴性。
⾸先我们来谈谈作为有向图的⻉叶斯⽹络是如何表达概率模型的,如下图所⽰:
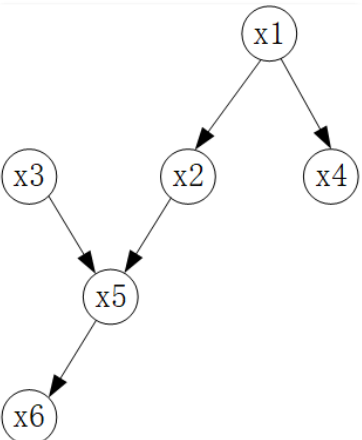
有向图中,每⼀个节点代表的都是随机变量,而⽗⼦节点之间带有⽅向性的箭头则表达为条件概率,它反映了⽗节点和⼦节 点之间的关系,在下⾯这个局部中:

在这个局部中, $x_i$是$x_j$的父节点, 因此这个图中$x_i. x_j$两个节点以及二者之间的有向关系则表示为条件概率:$p(x_j \mid x_i)$。
贝叶斯网络中的三种基本结构
实际上,在⻉叶斯⽹络中,⽆论节点有多少,看上去⽹络有多么复杂,实际上都是由三类基本结构(或者我们称之为基本组件)构成:
第一类是tail to tail结构:
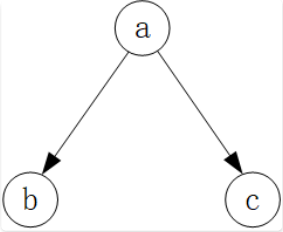
第二类是 head to tail结构:

第三类是 head to head 结构:
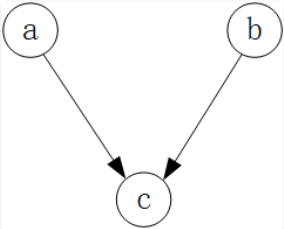
再复杂的⻉叶斯⽹络,拆解下来,⽆⾮就是这⼏类基本零件。
贝叶斯网络对联合概率的拆解
⻉叶斯⽹络中如何拆解联合概率$p(x_1, x_2, …, x_p)$,这就要借助我们在有向图中的⼀个定义, 即有向图的因⼦分解公式,利⽤它我们可以在有向图中, 将联合概率拆解成若干个条件概率连乘的形式,从而很好的解决高维随机变量概率的化简:
\[p(x_1, x_2, x_3, ..., x_p) = \prod_{i=1}^p p(x_i \mid x_{pa(i)})\]其中, $x_{pa(i)}$是$x_i$的⽗节点集合。
PS: 记住,这是个定义。
因⼦分解公式套⽤在最开始的六个节点的⻉叶斯⽹络图中,联合概率的表达式可以拆解为如下形式:
\[p(x_1, x_2, ..., x_6) = p(x_1)p(x_2 \mid x_1)p(x_3)p(x_4 \mid x_1)p(x_t \mid x_2, x_3)p(x_6 \mid x_5)\]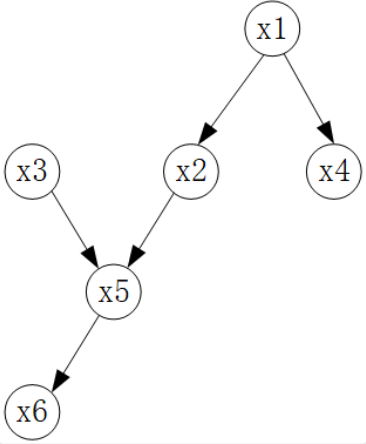
那我们进⼀步去深挖这个因⼦分解公式,实际上可以探究出⻉叶斯⽹络拓扑中,由其结构所蕴含的条件独⽴性质。
我们还是在三个基本结构中来看。
⾸先是 tail to tail 结构:
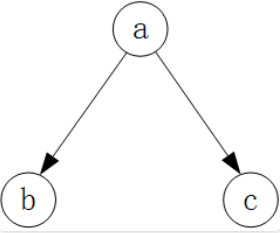
首先按照因子分解, 联合概率写作:
\[p(a, b, c) = p(a)p(b \mid a)p(c \mid a)\]再按照链式法则来表达联合概率:
\[p(a, b, c) = p(a)p(b \mid a)p(c \mid a, b)\]联立这两个式子:
\[p(a)p(b \mid a)p(c \mid a) = p(a)p(b \mid a)p(c \mid a, b)\]最终可以得到: $p(c \mid a) = p(c \mid a,b)$。
这是⼀个条件独⽴的表达,即在随机变量$a$给定的情况下, $b$的取值与否,不影响条件概率$p(c \mid a)$的取值,换句话说就是在给定$a$的条件下,随机变量$b$和$c$是相互独⽴的,记作:$b \perp c \mid a$ 。我们可以说 tail to tail 的结构就是和这种条件独⽴性是相对应的。
再看 head to tail 结构:
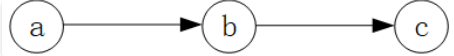
同样地,按照因⼦分解的公式和链式法则也可以得到联合概率的两种表达。
因子分解公式:
\[p(a, b, c) = p(a)p(b \mid a)p(c \mid b)\]链式法则:
\[p(a, b, c) = p(a)p(b \mid a)p(c \mid a, b)\]联立:
\[p(a)p(b \mid a)p(c \mid b) = p(a)p(b \mid a)p(c \mid a, b)\]最终可以得到: $p(c \mid b) = p(c \mid a, b)$, 即, 给定$b$的条件下, 随机变量$a$和$c$条件独立,记作:$a \perp c \mid b$。
沿着这个思路, 我们再来看 head to head 结构:
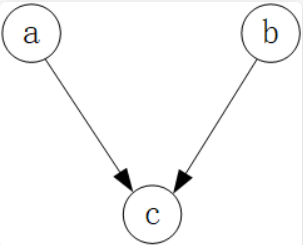
因子分解公式:
\[p(a, b, c) = p(a)p(b)p(c \mid a, b)\]链式法则:
\[p(a, b, c) = p(a)p(b \mid a)p(c \mid a, b)\]联立:
\[p(a)p(b)p(c \mid a, b) = p(a)p(b \mid a)p(c \mid a, b)\]最终得到:$p(b) = p(a \mid b)$, 似乎和前⾯相⽐有所不同,直接我们得到了随机变量 和 是独⽴的,即$a \perp b$而不需要给定$c$作为条件。
如果给定$c$作为条件,随机变量$a$和$b$是否满⾜条件独⽴性呢?答案是,不满⾜。
我们重点说明⼀下为什么在 head to head 这种结构下,不满⾜$a \perp b \mid c$ ,即$p(a \mid c) \neq p(a \mid b, c)$。
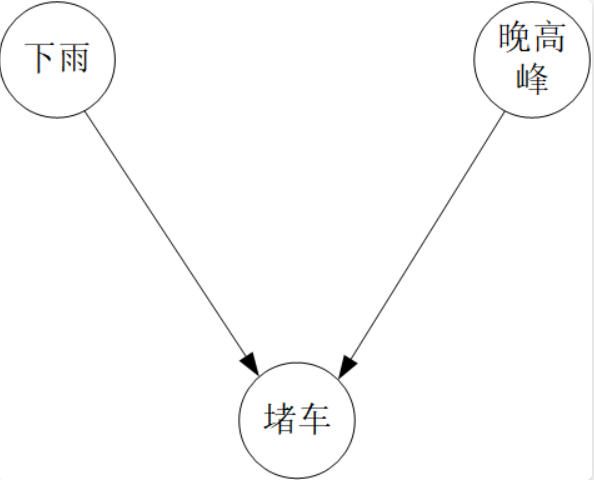
我们知道,下⾬和晚⾼峰都是造成堵⻋的原因,假设已知堵⻋的条件下,下⾬的概率为 ,我们假设它为 0.3,即$p(下雨 \mid 堵车) = 0.3$, 那么如果此时堵车, 但是是在晚高峰时期, 那下雨的概率肯定就小了, 因为晚高峰本身就可能带来堵车, 即$p(下雨 \mid 堵车, 晚高峰) < 0.3$, 显然下雨和晚高峰, 二者不满足给定堵车条件下的条件独立。
但是如果抛开堵⻋这个条件呢?那么下⾬和晚⾼峰,就是没啥关系的事⼉了,因此⼆者就是相互独⽴的。
贝叶斯网络与一些概率模型的关系
⻉叶斯⽹络, 就是朴素⻉叶斯模型。
引⼊隐含变量后, 介绍了⻉叶斯⽹络中的⼀种简单的带有隐变量的混合模型:混合⾼斯模型。
不要⽹络, 随机过程中的⻢尔科夫链和⾼斯过程也是⼀种⻉叶斯⽹络,它是带有时间轴的模型。
后续我们将时间轴和混合两个特征做⼀个结合,即同时具备时间轴特性和隐变量混合模型特性的模型,将是我们介绍的重 点,我们将依次展开隐⻢尔可夫模型、卡尔曼滤波和粒⼦滤波的介绍。