问题的提出
在工程应用及科学研究中,经常需要研究两个变量之间的函数关系$y=f(x)$.但常常不能得到$f(x)$的具体的解析表达式,它可能得到是一组试验数据$(x_i,y_i)( i=1,2,… ,n)$; 或者解析表达式相当复杂,不便于计算和使用,给问题的研究带来困难。
解决方案
寻找好一个计算简单的函数$S(x)$近似替代函数$f(x)$, 将研究$f(x)$的问题转换为研究$S(x)$。 当选用近似标准不同时, 就构成不同的方法。
- 插值法
- 最佳逼近和最小二乘法
定义(一维插值)
已知: 函数$f(x)$在区间$[a, b]$上$n+1$个互异节点$x_0, x_1, x_2, …, x_n$处的函数值$f(x_0), f(x_1), …, f(x_n)$。
求: 函数$S(x)$, 使得$S(x_i) = f(x_i) (i = 0, 1, 2, …, n)$
称: $S(x)$为$f(x)$关于点$x_i(i=0, 1, 2, …, n)$的插值函数, $x_i$为插值节点, $[a, b]$为插值区间, 求插值函数$S(x)$的方法为插值法。
$f(x) \approx S(x)$时, 误差函数$R(x) = f(x) - S(x)$为插值余项。
常用的插值函数
常用的插值函数: 多项式、有理分式、三角函数和指数函数。
由于多项式核分段多项式计算简单, 所以在工程计算中这两种插值函数使用最多。 当插值函数是次数不超过$n$次的多项式时, 称其为$n$次插值多项式。
\[P_n(x) = a_0 + a_1x + ... + a_nx^n\]PS: 有点麦克劳林公式的感觉, 这里$x$是已知量,求$a$。
定理: (插值多项式的存在唯一性)已知函数$f(x)$在$[a, b]$上的$n+1$个互异节点$x_i(i=0, 1, …, n)$处的函数值$f(x_i)(i=0, 1, …, n)$, 则存在唯一的插值多项式
\[P_n(x) = a_0 + a_1 x + a_2 x^2 + ... + a_n x^n\]使得$P_n(x_i) = f(x_i), (i=0, 1, 2, …, n)$
注1: 只要$n+1$个节点互异, 满足插值条件的$n$次插值多项式是存在、唯一的。
注2: 如果不限制多项式的次数, 插值多项式并不唯一。
插值多项式的构造方法
- 待定系数法: 计算工作量较大
- 常用插值方法
- 拉格朗日插值法
- 牛顿插值法
- 分段低次插值法
- 三次样条插值法
拉格朗日插值法
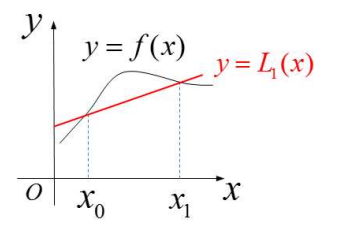
线性插值($n=1$, 一次插值)
| $x_i$ | $x_0$ | $x_1$ |
|---|---|---|
| $y_i$ | $y_0$ | $y_1$ |
求解$y = L_1(x) = a_0 + a_1 x$, 使得$L_1(x_i) = y_i, (i=0, 1)$
点斜式:
\[\begin{aligned} L_1 &= y_0 + \frac{y_1 - y_0}{x_1 - x_0}(x - x_0) \\ & = \frac{x-x_0}{x_1 - x_0}y_1 - \frac{x - x_0}{x_1 - x_0}y_0 + \frac{x_1 - x_0}{x_1 - x_0}y_0 \\ & = \frac{x-x_0}{x_1 - x_0}y_1 + \frac{x_0 - x}{x_1 - x_0}y_0 + \frac{x_1 - x_0}{x_1 - x_0}y_0 \\ & = \frac{x-x_0}{x_1 - x_0}y_1 + \frac{x_1 - x}{x_1 - x_0}y_0 \\ & = \frac{x - x_1}{x_0 - x_1}y_0 + \frac{x-x_0}{x_1 - x_0}y_1 \end{aligned}\]以直线代替曲线$f(x) \approx L_1(x)$
记
\[l_0(x) = \frac{x - x_1}{x_0 - x_1}, l_1(x) = \frac{x - x_0}{x_1 - x_0}\]则
\[L_1(x) = l_0(x)y_0 + l_1(x)y_1\]称函数$l_0(x)$和$l_1(x)$为节点$x_0, x_1$处的线性插值基函数。
此时插值基函数$l_0(x)$和$l_1(x)$都是线性函数, 且具有以下性质:
\[l_0(x) + l_1(x) = 1\] \[l_0(x_0) = 1, l_0(x_1) = 0, l_1(x_0) = 0, l_1(x_1) = 1\]思考: 为什么?
回答: 将$x_0$和$x_1$分别代入$l_0(x)$和$l_1(x)$就知道了。
二次插值($n=2$, 抛物线插值)
| $x_i$ | $x_0$ | $x_1$ | $x_2$ |
|---|---|---|---|
| $y_i$ | $y_0$ | $y_1$ | $y_2$ |
求解$y = L_2(x) = a_0 + a_1x + a_2 x^2$, 使得$L_2(x_i) = y_i, (i=0, 1, 2)$
构造抛物插值多项式:
\[L_2(x) = l_0(x)y_0 + l_1(x)y_1 + l_2(x)y_2\]其中插值基函数满足:
\[\begin{cases} l_0(x_0) = 1 \\ l_0(x_1) = 0 \\ l_0(x_2) = 0 \end{cases} \qquad \begin{cases} l_1(x_0) = 0 \\ l_1(x_1) = 1 \\ l_1(x_2) = 0 \end{cases} \qquad \begin{cases} l_2(x_0) = 0 \\ l_2(x_1) = 0 \\ l_2(x_2) = 1 \end{cases}\]要求的$l_i(x), i=1, 2, 3$均为二次多项式。
设
\[l_0(x) = A(x - x_1)(x - x_2)\]思考: 为什么能这么设呢?
回答:因为这是个二次多项式,感觉可以随便设,只要保证是二次多项式就好
由
\[l_0(x_0) = 1 \Rightarrow A(x_0 - x_1)(x_0 - x_2) = 1\]即
\[A = \frac{1}{(x_0 - x_1)(x_0 - x_2)}\]所以:
\[l_0(x) = \frac{(x - x_1)(x - x_2)}{(x_0 - x_1)(x_0 - x_2)}\]同理:
\[l_1(x) = \frac{(x - x_0)(x - x_2)}{(x_1 - x_0)(x_1 - x_2)}\] \[l_2(x) = \frac{(x - x_0)(x - x_1)}{(x_2 - x_0)(x_2 - x_1)}\]故
\[\begin{aligned} L_2(x) & = l_0(x)y_0 + l_1(x)y_1 + l_2(x)y_2 \\ & = \frac{(x - x_1)(x - x_2)}{(x_0 - x_1)(x_0 - x_2)}y_0 + \frac{(x - x_0)(x - x_2)}{(x_1 - x_0)(x_1 - x_2)}y_1 + \frac{(x - x_0)(x - x_1)}{(x_2 - x_0)(x_0 - x_1)}y_2 \end{aligned}\]验证知:
\[L_2(x_0) = y_0, L_2(x_1) = y_1, L_2(x_2) = y_2\]n次拉格朗日插值多项式
推广一次与二次插值多项式的构造方法, 可构造出由$n+1$个互异数组$(x_i, y_i)(i=0, 1, 2,…, n)$确定的$n$次插值多项式
\[L_n(x) = l_0(x)y_0 + l_1(x)y_1 + ... + l_n(x)y_n = \sum_{k=0}^n l_k(x)y_k\]其中
\[l_k = \frac{(x - x_0) ... (x - x_{k-1})(x - x_{k+1})...(x - x_n)}{(x_k - x_0) ... (x_k - x_{k-1})(x_k - x_{k+1})...(x_k - x_n)} = \prod_{i=0, i \neq k}^n \frac{x - x_i}{x_k - x_i}\]称为$n$次拉格朗日插值基函数, 满足:
\[l_j(x_k) = \begin{cases} 1 & k=j \\ 0 & k \neq j \end{cases} (j, k = 0, 1, ..., n)\]$L_n(x)$为$n$次拉格朗日插值多项式, 验证知$L_n(x_i) = y_i(i=0, 1, …, n)$。
插值余项和误差估计
定理: 设$f(x)$在$[a, b]$上有$n+1$阶连续导数, 则$n$次插值多项式$L_n(x)$对任意$x \in [a, b]$, 有插值余项
\[R_n(x) = f(x) - L_n(x) = \frac{f^{n+1}(\xi)}{(n+1)!}\omega_{n+1}(x)\]其中$\omega_{n+1}(x) = \prod_{i=0}^n(x - x_i), a < \xi < b(且依赖于x)$
特别地, 如果:
\[\max_{a \leq x \leq b} \mid f^{(n+1)}(x) \mid \leq M\]则插值多项式$L_n(x)$逼近$f(x)$的误差估计式:
\[\mid R_n(x)\mid \leq \frac{M}{(n+1)!}\mid \omega_{n+1}(x) \mid\]集中常用的低阶插值余项公式
当$n=1$时,
\[R_1(x) = f(x) - L_1(x) = \frac{1}{2} f''(\xi)(x - x_0)(x - x_1), \xi \in (a, b)\]当$n=2$,
\[R_2(x) = f(x) - L_2(x) = \frac{1}{3!} f'''(\xi)(x - x_0)(x - x_1)(x - x_2), \xi \in (a, b)\]拉格朗日插值的优缺点
- 拉格朗日插值基函数形式对称, 结构紧凑, 易分析、易编程; 节点处函数值变化时,基函数不变, 可用于不同批次的数据插值。
- 当插值节点的个数改变时,插值基函数$l_k(x)(k=0, 1, …, n)$均要随之变化, 整个公式也要发生变化,计算结果无继承性,效率低。
改进方案:牛顿插值法
拉格朗日插值法代码
1
2
3
4
5
6
7
8
9
10
11
12
13
from scipy import integrate
import sympy
def f(x):
return sympy.exp(- x ** 2)
def integral(f, low, high):
y, err = integrate.quad(f, low, high)
y1, err1 = integrate.quad(f, 0, 1)
print(f"积分下限为0, 上限为1的积分结果: {y1}")
y2, err2 = integrate.quad(f, 0, 2)
print(f"积分下限为0, 上限为2的积分结果: {y2}")
输出:
1
2
积分下限为0, 上限为1的积分结果: 0.7468241328124271
积分下限为0, 上限为2的积分结果: 0.8820813907624215
Lagrange插值法公式:
\[L_n(x) = l_0(x)y_0 + l_1(x)y_1 + ... + l_n(x)y_n = \sum_{k=0}^n l_k(x)y_k\]其中:
\[l_k(x) = \prod_{i=0, i \neq k} \frac{(x - x_i)}{x_k - x_i}\]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
X = [1, 2]
w = [0.7468241328124271, 0.8820813907624215]
def lagrange(x, w):
M = len(x)
p = 0.0
for j in range(M):
pt = w[j]
for k in range(M):
if k == j:
continue
fac = x[j]-x[k]
pt *= np.poly1d([1.0, -x[k]])/fac
p += pt
return p
print(f"拉格朗日插值{lagrange(X, w)}")
输出
1
2
拉格朗日插值:
0.1353 x + 0.6116
拉格朗日插值余项
\[R_n(x) = f(x) - L_n(x) = \frac{f^{(n+1)(\xi)}}{(n+1)!}\prod_{i=0}^n(x - x_i)\] \[R_1 = \frac{1}{2!}\mid f^{(2)}(\xi)(x - 1)(x - 2)\mid \leq \frac{1}{2} f^{(2)}(1)(x - 1)(x-2), \xi \in (1, 2)\]1
2
3
4
5
6
7
8
9
10
11
#求导使用diff方法
x = sympy.Symbol('x')
f = sympy.exp(-x**2)
f1 = sympy.diff(f, x)
print(f"原式的二阶导数等于: {f1}")
# 计算1时的二阶导数值
result=f1.evalf(subs={x:1})
R1 = 1/2 * sympy.Abs(result * (x - 1) * (x - 2))
print(f"误差为: {R1}")
输出
1
2
原式的二阶导数等于: -2*x*exp(-x**2)
误差为: 0.5*Abs((0.735758882342885*x - 0.735758882342885)*(x - 2))