作为机器学习科学家，我们的目标是发现模式。但是我们怎么能确定我们真的发现了一个普遍的模式，而不是简单地记忆我们的数据呢？例如，想象一下，我们想在将患者与其痴呆状态联系起来的遗传标记中寻找模式，其中标签是从集合 ${\text{dementia, mild cognitive impairment, healthy}}$ 中提取的 。因为每个人的基因都是独一无二的(忽略双胞胎)，所以有可能记住整个数据集。

我们不希望我们的模型说 “That ‘ s Bob! 我记得他! 他痴呆!” 原因很简单。当我们将来部署模型时，我们将遇到模型以前从未见过的病人。只有当我们的模型真正发现了一种普遍模式时，我们的预测才会有用。

更正式地概括一下，我们的目标是发现能够捕捉到我们的训练集所来自的潜在人群中的规律的模式。如果我们在这方面取得了成功，即使是对我们从未遇到过的个人, 我们也可以成功地评估风险。如何发现泛化的模式是机器学习的基本问题。

危险在于，当我们训练模型时，我们只访问一小部分数据样本。最大的公共图像数据集大约包含100万张图像。更多的时候，我们必须从成千上万的数据例子中学习。在一个大型医院系统中，我们可能会访问成千上万的医疗记录。在使用有限样本时，我们可能会冒着这样的风险：当我们收集更多的数据时，我们可能会发现一些明显的关联，而这些关联最终不会成立。

对训练数据的拟合比对基础分布的拟合更接近的现象称为过拟合，而用于对抗过拟合的技术称为正则化。在前面几节中，您可能在使用fashionn - mnist数据集进行实验时观察到了这种效果。如果你在实验中改变模型结构或超参数，你可能已经注意到，有足够的神经元、层次和训练周期，模型最终可以在训练集上达到很高的准确性， 但测试数据的准确性下降。

Training Error and Generalization Error

为了更正式地讨论这一现象，我们需要区分训练误差和泛化误差。 训练误差是我们的模型在训练数据集上计算的误差， 泛化误差是模型误差的期望， 如果我们将其应用于从与原始样本相同的底层数据分布中提取的无限多个数据样本流。

问题是，我们永远不能准确地计算泛化误差。这是因为无限数据流是一个虚构的目标。在实践中，我们必须将我们的模型应用于一个独立的测试集，该测试集由一个从我们的训练集中保留的随机选择的数据样本组成。

下面的三个思维实验将有助于更好地说明这种情况。考虑一个大学生准备他的期末考试。一个勤奋的学生会努力练习，用往年的考试来测试自己的能力。尽管如此，在过去的考试中取得好成绩并不能保证他在关键时刻就能脱颖而出。例如，学生可能试图通过死记硬背考试问题的答案来准备。这要求学生记住很多东西。她甚至可能完全记得过去考试的答案。另一个学生可能会通过试着理解给出某些答案的原因来准备。在大多数情况下，后者会做得更好。

同样，考虑一个仅使用查找表来回答问题的模型。如果允许的输入集是离散的且相当小，那么在查看了许多训练样本之后，这种方法可能会执行得很好。然而，当面对它从未见过的例子时，这个模型仍然没有能力比随机猜测做得更好。在现实中，输入空间太大了，无法记住每一个可以想到的输入对应的答案。例如， 考虑一个 $28 \times 28$ 的灰度图像。 如果每个像素的灰度值都可以在0到256之间， 那么将会有 $256^{784}$ 个可能的图像。这意味着低分辨率的灰度图比宇宙中原子的数量要多得多。即使我们遇到了这样的数据， 我们将无法存储查找表。

最后，考虑如何根据一些可能的上下文特征对抛硬币的结果进行分类(class 0: heads, class 1: tails)。假设硬币是均匀的。不管我们用什么算法，泛化误差都会是 $\frac{1}{2}$。 然而，对于大多数算法，我们应该期望我们的训练错误相当低，这取决于抽样的运气，即使我们没有任何特征！假设数据集 ${0, 1, 1, 1, 0, 1}$ 。 我们的无特征算法将不得不总是预测大多数类别，从我们有限的样本来看，这似乎是1。在这种情况下，总是预测第1类的模型将产生 $\frac{1}{3}$ 的误差，这比我们的泛化误差要好得多。随着数据量的增加，正面的比例显着偏离 $\frac{1}{2}$ 的概率会降低，我们的训练误差将与泛化误差相匹配。

Statistical Learning Theory

由于泛化是机器学习的基本问题，你可能不会感到惊讶，许多数学家和理论家已经致力于发展形式理论来描述这一现象。在他们的同名定理中，Glivenko和Cantelli推导了训练误差收敛到泛化误差的速率。在一系列开创性的论文中，Vapnik和Chervonenkis将这一理论扩展到更一般的函数类。这项工作奠定了统计学习理论的基础。

在标准监督学习设置中，我们到目前为止已经讨论过，并将在本书的大部分内容中继续讨论，我们假设训练数据和测试数据都是独立同分布的。这通常被称为i.i.d.假设，这意味着对我们的数据进行采样的过程没有记忆。换句话说，采样的第二个样本和第三个样本的相关性并不比采样的第二个和第200万个样本的相关性高。

成为一名优秀的机器学习科学家需要批判性地思考，并且您已经应该在这个假设中找到漏洞，提出假设失败的常见情况。如果我们根据从加州大学旧金山分校医疗中心收集的患者数据训练一个死亡风险预测器，并将其应用于麻省总医院的患者会怎样？这些分布并不完全相同。此外，采样可能在时间上是相关的。如果我们对推文的主题进行分类怎么办？ 新闻周期会在所讨论的主题中产生时间依赖性，违反任何独立性假设。

有时，我们可能会稍微违反i.i.d.假设，但我们的模型将继续出色地工作。毕竟，几乎每个现实世界的应用程序都至少涉及一些对 i.i.d 假设的轻微违反，但我们有许多有用的工具用于各种应用程序，例如人脸识别、语音识别和语言翻译。

其他违规行为肯定会引起麻烦。 想象一下，例如，如果我们试图通过专门针对大学生的训练来训练一个人脸识别系统，然后想要将其部署为监控疗养院人群中老年病的工具。这不太可能奏效，因为大学生往往看起来与老年人有很大不同。

在随后的章节中，我们将讨论由于违反i.i.d.假设而产生的问题。目前，即使将i.i.d.假设视为理所当然，理解泛化也是一个艰难的问题。此外，阐明为什么深度神经网络能泛化的精确理论基础 困扰着学习理论中最伟大的思想。

当我们训练我们的模型时，我们试图搜索一个尽可能适合训练数据的函数。如果该函数非常灵活，可以像捕捉真实关联一样容易地捕捉到虚假模式，那么它可能会表现得太好，而不会生成一个能够很好地概括未知数据的模型。这正是我们想要避免或至少控制的。深度学习中的许多技术都是旨在防止过度拟合的启发式方法和技巧。

Model Complexity

当我们有简单的模型和丰富的数据时，我们期望泛化误差与训练误差相似。当我们使用更复杂的模型和更少的例子时，我们预计训练误差会下降，但泛化差距会增加。究竟是什么构成了模型的复杂性是一个复杂的问题。许多因素决定着一个模型是否能够很好地泛化。例如，具有更多参数的模型可能被认为更复杂。参数取值范围更大的模型可能更复杂。通常对于神经网络，我们认为需要更多训练迭代的模型更复杂，而需要尽早停止(更少的训练迭代)的模型更不复杂。

很难比较本质上不同的模型类(比如决策树和神经网络)成员之间的复杂性。目前，一个简单的经验法则非常有用：一个可以轻松解释任意事实的模型是统计学家认为复杂的，而表达能力有限但仍能很好地解释数据的模型可能更接近事实 。在哲学中，这与波普尔关于科学理论的可证伪性标准密切相关：一个理论是好的，如果它拟合数据并且有可以用来反驳它的具体测试。这一点很重要，因为所有的统计估计都是事后的，也就是说，我们是在观察事实后才进行估计的，因此容易受到相关谬误的影响。目前，我们将把哲学放在一边，继续更具体的问题。

在本节中，为了给您一些直观的感觉，我们将重点关注一些可能影响模型类的通用性的因素：

• 可调参数的数量。当可调参数的数量(有时称为自由度)很大时，模型往往更容易受到过拟合的影响。
• 参数所取的值。当权重可以取更大范围的值时，模型可能更容易过拟合。
• 训练样本的数量。即使您的模型很简单，也很容易过拟合只包含一两个样本的数据集。但是过拟合一个有数百万个例子的数据集需要一个非常灵活的模型。

Model Selection

Underfitting or Overfitting?

Model Complexity

为了说明关于过拟合和模型复杂性的一些经典直觉，我们给出了一个使用多项式的例子。给定由单一特征 $x$ 和相应实值标号 $y$ 组成的训练数据，我们试图找到 $d$ 次多项式。

为了估计标签 $y$。 这是一个线性回归问题， 其中我们的特征是 $x$ 的幂， 模型的权重由 $w_i$ 给定，因为 $x^0 = 1$， 偏差由 $w_0$ 给定 。因为这只是一个线性回归问题，我们可以用平方误差作为损失函数。高阶多项式函数比低阶多项式函数复杂，因为高阶多项式具有更多的参数，模型函数的选择范围更广。固定训练数据集，相对于低次多项式，高次多项式函数应该总是获得较低的(最坏的情况是相等的)训练误差。事实上，当每个数据样本都有不同的值 $x$ 时，一个次数等于数据样本个数的多项式函数可以很好地拟合训练集。我们可视化的多项式度与欠拟合和过拟合之间的关系如图 4.4.1.

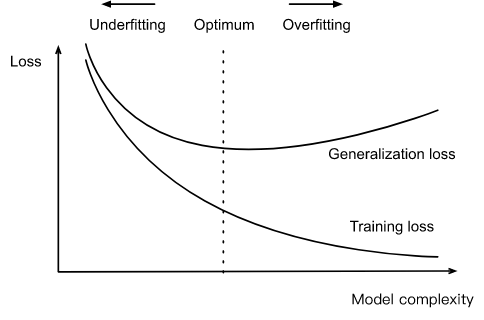
图 4.1.1 模型复杂度对欠拟合和过拟合的影响

• Previous
  【d2l】Multilayer Perceptrons
• Next
  【深度学习】XMC-GAN： Cross-Modal Contrastive Learning for Text-to-Image Generation