贝叶斯决策理论
统计模式识别: 用概率统计的观点和方法解决模式识别的问题。
贝叶斯决策(统计决策理论):
- 是统计模式识别的基本方法和基础
- 是 “最优分类器”: 使平均错误率最小
条件:
- 类别数一定, $w_i, i=1, …, c$ (决策论中把类别称作状态)
- 已知类先验概率和类条件概率密度 $P(w_i), P(x \mid w_i), i=1, …, c$
最小错误率贝叶斯决策
\[\min P(e) = \int P(e \mid x)p(x)dx\]上式等价于 $\min P(e \mid x) \quad \text{for all } x$。
而
\[P(e \mid x) = \begin{cases} P(w_2 \mid x) & \text{if assign } x \in w_1 \\ P(w_1 \mid x) & \text{if assign } x \in w_2 \end{cases}\]最小错误率贝叶斯决策,简称贝叶斯决策。
如何计算后验概率?
已知 $P(w_i), p(x \mid w_i), i=1,2$
贝叶斯公式 (Bayesian Theory):
\[P(w_i \mid x) = \frac{p(x \mid w_i)P(w_i)}{p(x)} = \frac{p(x \mid w_i)P(w_i)}{\sum_{j=1}^2 p(x \mid w_j)P(w_j)}, i=1, 2\] \[if \quad P(w_1 \mid x) \begin{cases} >\\ < \end{cases} P(w_2 \mid x) \quad \text{then assign } \begin{cases} x \in w_1 \\ x \in w_2 \end{cases}\]最小错误率贝叶斯决策规则的几种等价表达形式:
- if $P(w_i \mid x) = \max_{j=1, 2} P(w_j \mid x)$, then $x \in w_i$
- if $p(x \mid w_i)P(w_i) = \max_{j=1,2}p(x \mid w_j)P(w_j)$, then $x \in w_i$
- if $l(x) = \frac{p(x \mid w_1)}{p(x \mid w_2)} \begin{cases}> \ <\end{cases} \frac{P(w_2)}{P(w_1)}$, then $x \in \begin{cases}w_1 \ w_2\end{cases}$
- 定义 $h(x) = -\ln[l(x)] = -\ln p(x \mid w_1) + \ln p(x \mid w_2)$
其中 $l(x)$ : 似然比; $\frac{P(w_2)}{P(w_1)}$: 似然比阈值; $h(x)$ : 对数似然比
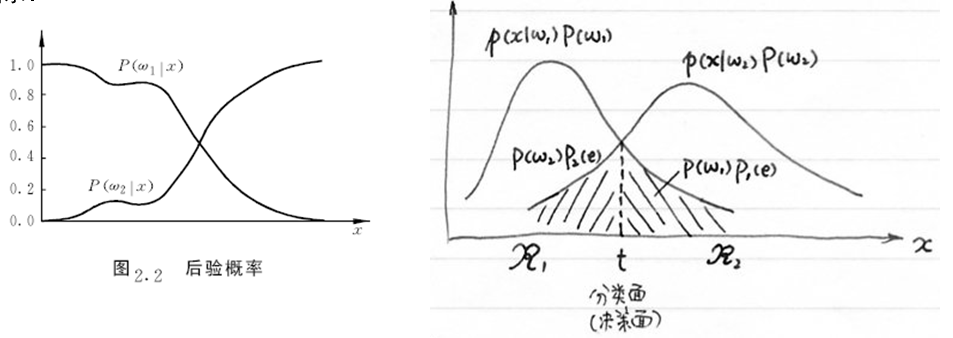
错误率:
\[\begin{aligned} P(e) &= P(w_2)P_2(e) + P(w_1)P_1(e) \\ &= P(w_2) \int _{\mathbb{R_1}} p(x \mid w_2)dx + P(w_1) \int_{\mathbb{R_2}}p(x \mid w_1)dx \end{aligned}\]最小风险贝叶斯决策
- 最小错误率只考虑了错误
- 进一步可考虑不同错误所带来的的损失(代价)
用决策论方法把问题表述如下:
- 把样本 $x$ 看做 $d$ 维随机向量 $x = [x_1, x_2, …, x_d]^T$
- 状态空间$\Omega$由 $c$ 个可能的状态 ($c$ 类)组成: $\Omega = {w_1, w_2, …, w_c}$
- 对随机向量 $x$ 可能采取的决策组成了决策空间, 它由 $k$ 个决策组成:
- 对于实际状态为 $w_j$ 的向量 $x$, 采取决策 $\alpha_i$ 所带来的的损失为:
形成损失函数
对于实际问题, 损失函数通常以表格形式给出(决策表)。
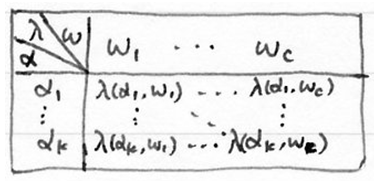
条件期望损失: 对于特定的 $x$ 采取决策 $\alpha_i$ 的期望损失:
\[R(\alpha_i \mid x) = E[\lambda(\alpha_i, w_j) \mid x] = \sum_{j=1}^c \lambda(\alpha_i, w_j)P(w_j \mid x), i=1, ..., k\]期望风险:对所有可能的 $x$ 采取决策 $\alpha(x)$ 所造成的期望损失之和。
\[R(\alpha) = \int R(\alpha(x) \mid x) p(x)dx\]也称平均风险。 ($R(\alpha)$ 表示 $R$ 依赖于决策规则 $\alpha(·)$)
最小风险决策: $\min R(\alpha)$ —— 期望风险最小化
对所有 $x$, 使 $R(\alpha(x) \mid x)$ 最小, 则可以使 $R(\alpha)$ 最小, 因此有:
最小风险贝叶斯决策规则:
\[if \quad R(\alpha_i \mid x) = \min_{j=1, ..., k} R(\alpha_j \mid x), \text{then } \alpha = \alpha_i\]计算: 可采取以下步骤(对于给定的样本 $x$):
1) 计算后验概率:
\[P(w_j \mid x) = \frac{p(x \mid w_j)P(w_j)}{\sum_{i=1}^c p(x \mid w_i)P(w_i)}, j=1, ..., c\]2) 计算风险:
\[R(\alpha_i \mid x) = \sum_{j=1}^c \lambda(\alpha_i \mid w_j)P(w_j \mid x), j=1, ..., k\]3) 决策:
\[\alpha = \arg \min_{i=1, ..., k} R(\alpha_i \mid x)\]两类情况: (损失函数 $\lambda_{11}, \lambda_{12}, \lambda_{21}, \lambda_{22}$)
\[\lambda_{11}P(w_1 \mid x) + \lambda_{12}P(w_2 \mid x) \begin{cases} > \\ < \end{cases} \lambda_{21}P(w_1 \mid x) + \lambda_{22}P(w_2 \mid x), \text{then } x \in \begin{cases}w_1 \\ w_2\end{cases}\]当 $\lambda_{11} = \lambda_{22} = 0$, $\lambda_{12} = \lambda_{21} =1$ 时, 最小风险就是最小错误率。

解:
\[P(w_1 \mid x) = \frac{p(x \mid w_1)P(w_1)}{\sum_{j=1}^2 p(x \mid w_j)P(w_j)}= \frac{0.2 \times 0.9}{0.2 \times 0.9 + 0.4 \times 0.1} = 0.818\] \[P(w_2 \mid x) = 1 - P(w_1 \mid x) = 0.182\] \[P(w_1 \mid x) = 0.818 > P(w_2 \mid x) = 0.182\]所以 $x \in w_1$

解:
已计算出的后验概率:
\[P(w_1 \mid x) = 0.818 \qquad P(w_2 \mid x) = 0.182\]条件风险:
\[R(\alpha_1 \mid x) = \sum_{j=1}^2 \lambda_{1j}P(w_j \mid x) = \lambda_{12}P(w_2 \mid x) = 1.092 \\ R(\alpha_2 \mid x) = \lambda_{21} P(w_1 \mid x) = 0.818\]由于 $R(\alpha_1 \mid x) > R(\alpha_2 \mid x)$, 决策为 $w_2$, 即 判别待识别的细胞为异常细胞。

MAP:
\[P(w_1 \mid x) = 0.4 < P(w_2 \mid x) = 0.6\]故判 $x$ 为鲑鱼
MR:
\[R(\alpha_1 \mid x) = 0 \times 0.4 + 1 \times 0.6 = 0.6 \leq R(\alpha_2 \mid x) = 2 \times 0.4 + 0 \times 0.6 = 0.8\]故判 $x$ 为鲈鱼。
概率密度函数的估计
贝叶斯决策: 已知 $P(w_i)$ 和 $p(x \mid w_i)$, 对未知样本分类(设计分类器)
实际问题: 已知一定数目的样本 ,对未知样本分类(设计分类器)
一种很自然的想法:
- 首先根据样本估计 $p(x \mid w_i)$ 和 $P(w_i)$, 记 $\hat p(x \mid w_i)$ 和 $\hat P(w_i)$
- 然后用估计的概率密度设计贝叶斯分类器
基于样本的两步贝叶斯决策
重要前提:
- 训练样本的分布能代表样本的真实分布, 所谓i.i.d条件
- 有充分的训练样本
参数方法
最大似然估计(Maximum Likelihood Estimation)
假设条件:
- 参数 $\theta$ 是确定的未知量(不是随机量)
- 各类样本集 $\mathcal{X}_i, i=1, …, c$中的样本都是从密度为 $p(x \mid w_i)$ 的总体重独立抽取出来的(独立同分布, i.i.d.)
- $p(x \mid w_i)$具有某种确定的函数形式, 只是其参数 $\theta$ 未知
- 各类样本只包含本类分布的信息
其中, 参数$\theta$通常是向量, 比如一维正态分布 $N(\mu_i, \sigma_i^2)$, 未知参数可能是 $\theta_i = \left[\begin{matrix}\mu_i \ \sigma_i^2\end{matrix}\right]$, 此时 $p(x \mid w_i)$ 可写成 $p(x \mid w_i, \theta_i)$ 或 $p(x \mid \theta_i)$。
鉴于上述假设, 我们可以只考虑一类样本, 记已知样本为:
\[\mathcal{X} = \{x_1, x_2, ..., x_N\}\]似然函数(likelihood function)
\[l(\theta) = p(\mathcal{X} \mid \theta) = p(x_1, x_2, ..., x_N \mid \theta) = \prod_{i=1}^N p(x_i \mid \theta)\]在参数 $\theta$ 下观测到样本集 $\mathcal{X}$ 的联合概率密度。
基本思想:
如果在参数 $\theta = \hat \theta$ 下 $l(\theta)$ 最大, 则 $\hat \theta$ 应是 “最可能” 的参数值, 它是样本集的函数, 记作 $\hat \theta = d(x_1, x_2, …, x_N) = d(\mathcal{X})$。 称作最大似然估计量。
为了便于分析, 还可以定义对数似然函数 $H(\theta) = \ln l(\theta)$
求解:
若似然函数满足连续、可微的条件, 则最大似然估计量就是方程:
\[\partial l(\theta) / \partial\theta = 0 \qquad \text{或} \qquad \partial H(\theta) / \partial \theta = 0\]的解(必要条件)。
若未知参数不止一个, 即 $\theta = [\theta_1, \theta_2, …, \theta_s]^T$, 记梯度算子
\[\nabla_\theta = \left[\frac{\partial}{\partial \theta_1}, \frac{\partial}{\partial \theta_2}, ..., \frac{\partial}{\partial \theta_s}\right]^T\]则最大似然估计量的必要条件由 S 和方程组成:
\[\nabla_\theta H(\theta) = 0\]讨论:
- 如果$l(\theta)$ 或 $H(\theta)$ 连续、可微, 存在最大值, 且上述必要条件方程组有唯一解, 则其解就是最大似然估计量。 (比如多元正态分布)。
- 如果必要条件有多解, 则需从中求似然函数最大者
- 若不满足条件, 则无一般性方法, 用其它方法求最大
正态分布下的最大似然估计示例
以单变量正态分布为例:
\[\theta = [\theta_1, \theta_2]^T, \theta_1=\mu, \theta_2 = \sigma^2\] \[p(x \mid \theta) = \frac{1}{\sqrt{2 \pi \sigma}} \exp\left[-\frac{1}{2} (\frac{x - \mu}{\sigma})^2\right]\]样本集 : $\mathcal{X} = {x_1, x_2, …, x_N}$
似然函数: $l(x) = p(\mathcal{X} \mid \theta) = \prod_{k=1}^N p(x_k \mid \theta)$
对数似然函数:
\[H(\theta) = \ln l(x) = \sum_{k=1}^N \nabla_\theta \ln p(x_k \mid \theta) = 0\]最大似然估计量 $\hat \theta$ 满足方程
\[\nabla_\theta H(\theta) = \sum_{k=1}^N \nabla_\theta \ln p(x_k \mid \theta) = 0\]而:
\[\ln p(x_k \mid \theta) = -\frac{1}{2} \ln 2 \pi \theta_2 - \frac{1}{2\theta_2}(x_k - \theta_1)^2\]Q:为什么是 $\theta_2$ 而不是 $\theta_2^2$ ?
A: 因为前面定义了 $\theta_2 = \sigma^2$
\[\nabla_\theta \ln p(x_k \mid \theta) = \left[\begin{matrix} \frac{1}{\theta_2}(x_k - \theta_1) \\ -\frac{1}{2\theta_2} + \frac{1}{2 \theta_2^2}(x_k - \theta_1)^2\end{matrix}\right]\]得方程组:
\[\begin{cases} \sum_{k=1}^N \frac{1}{\hat \theta_2}(x_k - \hat \theta_1) = 0 \\ -\sum_{k=1}^N \frac{1}{\hat \theta_2} + \sum_{k=1}^N \frac{(x_k - \hat \theta_1)^2}{\theta_2^2} = 0 \end{cases}\]解得:
\[\hat \mu = \hat \theta_1 = \frac{1}{N} \sum_{k=1}^N x_k\] \[\hat \sigma^2 = \hat \theta_2 = \frac{1}{N} \sum_{k=1}^N (x_k -\hat \mu)^2\]贝叶斯估计和贝叶斯学习(Bayesian Estimation and Bayesian Learning)
贝叶斯估计与贝叶斯决策类似, 只是练得决策状态变成了连续的估计。
基本思想
把待估计参数 $\theta$ 看做具有先验分布 $p(\theta)$ 的随机变量, 其取值与样本集 $\mathcal{X}$ 有关, 根据样本集 $\mathcal{X} = {x_1, x_2, …, x_N}$ 估计 $\theta$。
损失函数: 把 $\theta$ 估计为 $\hat theta$ 所造成的的损失, 记为 $\lambda(\hat \theta, \theta)$。
期望风险:
\[\begin{aligned} R &= \int_{E^d} \int_{\Theta} \lambda(\hat \theta, \theta) p(\theta \mid x) d \theta \\ &= \int_{E^d} \int_{\Theta} \lambda(\hat \theta, \theta) p(\theta \mid x) p(x) d \theta dx \\ &= \int_{E^d} R(\hat \theta \mid x) p(x) dx \end{aligned}\]其中 $x \in E^d, \theta \in \Theta$
条件风险: $R(\hat \theta \mid x) = \int_\Theta \lambda(\hat \theta, \theta)p(\theta \mid x)d\theta, x \in E^d$
最小化期望风险 $\Rightarrow$ 最小化条件风险
有限样本集下, 最小化经验风险:
\[R(\hat \theta \mid \mathcal{X}) = \int_\Theta \lambda(\hat \theta, \theta)p(\theta \mid \mathcal{X}) d \theta\]贝叶斯估计量: (在样本集 $\mathcal{X}$ 下) 使条件风险 (经验风险) 最小的估计量 $\hat \theta$。
损失: 离散情况: 损失函数表(决策表);
连续情况: 损失函数;
常用的损失函数: $\lambda(\hat \theta, \theta) = (\theta - \hat \theta)^2$
定理
如果采用平方误差损失函数, 则 $\theta$ 的贝叶斯估计量 $\hat \theta$ 是在给定 $x$ 时的条件期望, 即
\[\hat \theta = E[\theta \mid x] = \int_\Theta \theta p(\theta \mid x) d \theta\]同理可得到, 在给定样本集 $\mathcal{X}$ 下, $\theta$ 的贝叶斯估计是:
\[\hat \theta = E[\theta \mid \mathcal{X}] = \int_\Theta p(\theta \mid \mathcal{X}) d \theta\]求贝叶斯估计的方法: (平方误差损失下)
1) 确定 $\theta$ 的先验分布 $p(\theta)$
2) 求样本集的联合分布
\[p(\mathcal{X} \mid \theta) = \prod_{i=1}^N p(x_i \mid \theta)\]3) 求 $\theta$ 的后验分布
\[p(\theta \mid \mathcal{X}) = \frac{p(\mathcal{X} \mid \theta)p(\theta)}{\int_{\Theta}p(\mathcal{X} \mid \theta)p(\theta) d \theta}\]4) 求 $\theta$ 的贝叶斯估计量
\[\hat \theta = \int_{\Theta} \theta p(\theta \mid \mathcal{X}) d \theta\]我们也可直接推断总体分布
\[p(x \mid \mathcal{X}) = \int_\Theta p(x \mid \theta) p(\theta \mid \mathcal{X}) d \theta\]其中:
\[p(\theta \mid \mathcal{X}) = \frac{p(\mathcal{X} \mid \theta)p(\theta)}{\int_\Theta p(\mathcal{X} \mid \theta)p(\theta) d \theta}\]设 $\theta$ 的最大似然估计为 $\hat \theta_l$, 则在 $\theta = \hat \theta_l$ 处 $p(\theta \mid \mathcal{X})$ 很可能有一尖峰, 若如此, 且先验概率 $p(\theta)$ 在 $\hat \theta_l$ 处非零且在附近变化不大, 则:
\[p(x \mid \mathcal{X}) \mathop{=}^· p(x \mid \hat \theta_l)\]即贝叶斯估计结果与最大似然估计结果近似相等。
如 $p(\theta \mid \mathcal{X})$ 的峰值不尖锐, 则不能用最大似然估计来替代贝叶斯估计。
最大似然估计和贝叶斯估计的比较
ML估计:
- 参数为未知确定变量
- 没有利用参数先验信息
- 估计的概率模型与假设模型一致
- 可解释性好
- 计算简单
贝叶斯估计:
- 参数为未知随机变量
- 利用参数的先验信息
- 估计的概率模型相比于假设模型会发生变化
- 可理解性差
- 计算复杂
## 非参数方法
直方图方法
非参数概率密度估计的最简单方法
- 把 $x$ 的每个分量分成 $k$ 个 等间隔小窗, (若 $x \in E^d$, 则形成 $k^d$ 个小窗)
- 统计落入各个小舱内的样本数 $q_i$
- 相应小窗的概率密度为 $q_i / (NV)$ ($N$:样本总数, $V$:小窗体积)
概率密度的估计:
\[\hat P = \frac{k}{NV}\]三种方法:
- 直方图:窗口位置、大小固定, 平均概率密度
- Parzen窗:滑动窗口、窗口大小固定, 使用滑动窗口估计每个点的概率密度
- K近邻分类(K-NN): 滑动窗口、窗口大小不固定, 窗口内样本数固定,使用滑动窗口估计每个点的概率密度
线性分类器
Fisher 线性判别分析
输入: 数据集 $D = {(x_1, y_1), (x_2, y_2), …, (x_m, y_m)}$, 其中任意样本 $x_i$ 为 $n$ 维向量, $y_i \in {C_1, C_2, …, C_k}$, 降维到的维度 $d$。
输出:降维后的样本集 $D’$
1) 计算类内散度矩阵 $S_w$
2) 计算类间散度矩阵 $S_b$
3) 计算矩阵 $S_w^{-1}S_b$
4) 计算 $S_w^{-1}S_b$ 的最大的 $d$ 个特征值和对应的 $d$ 个特征向量 $(w_1, w_2, …, w_d)$, 得到投影矩阵
5) 对样本集中的每一个样本特征 $x_i$, 转化为新的样本 $z_i = W^T x_i$
6) 得到输出样本集 $D’ = {(z_1, y_1), (z_2, y_2), …, (z_m, y_m)}$
LDA vs PCA
相同点:
- 两者均可以对数据进行降维
- 两者在降维时均使用了矩阵特征分解的思想
- 两者都假设数据符合高斯分布
不同点:
- LDA是有监督的降维方法, 而PCA是无监督的降维方法
- LDA降维最多降到类别数 C-1 的维数, 而PCA没有这个限制
- LDA除了可以用于降维, 还可以用于分类
- LDA选择分类性能最好的投影方向, 而PCA选择样本点投影具有最大方差的方向
非线性分类器
支持向量机
SVM有三宝 : 间隔、对偶、核技巧
SVM:
- hard-margin SVM: 最大间隔分类器
- soft-margin SVM
- kernel SVM
$w^T x + b$ 是一个超平面, sgn 为符号函数, 因此SVM是一个判别模型。
hard-margin SVM: 最大间隔分类器
对于 ${x_i, y_i}_{i=1}^N$, $x_i \in \mathbb{R}^p, y_i \in {-1, 1}$
\[\max \text{margin} (w, b), \qquad \text{s.t.} \begin{cases} w^Tx_i + b > 0, & y_i = +1 \\ w^T x_i + b < 0, & y_i = -1 \end{cases} \Leftrightarrow y_i(x^T x_i + b) > 0, i = 1, 2, ..., N\] \[\text{margin} (w, b) = \min_{w, b, x_i, i=1, ..., N} \text{distance}(w, b, x_i)\] \[\text{distance} = \frac{1}{\| w \|} \mid w^T x + b \mid\]这个公式是点到直线的距离, 初中所学为:
\[\text{distance} = \mid \frac{Ax_0 + By_0 + C}{\sqrt{A^2 + B^2}} \mid\]公式中直线方程为 Ax + By + C = 0, 点 $P$ 的坐标为 $(x_0, y_0)$。 将$w$ 看做 $(A, B)$ 向量, $x$ 看做 $(x_0, y_0)$向量, $C$ 看做 $b$, $\sqrt{A^2 +B^2}$ 是 $w$ 的L2范数。
因此, 最终
\[\begin{aligned} & \max_{w, b} \min_{x_i, i=1, ..., N} \frac{1}{\|w\|} y_i(w^T x_i + b), \quad \text{s.t.} \quad y_i(w^Tx_i +b) > 0 \\ &= \max_{w, b} \frac{1}{\|w\|} \min_{x_i, i=1, ..., N} y_i (w^Tx_i + b) \quad \exists \gamma > 0, \text{s.t.} \min_{x_i, y_i, i=1, ..., N} y_i(w^T x_i + b) = \gamma \end{aligned}\]因为直线是可以等比例缩放的, 因此我们令 $\gamma = 1$, :
\[\min_{x_i, y_i, i=1, ..., N} y_i(w^T x_i + b) = 1\]那么
\[\max_{w, b} \frac{1}{\|w\|} \qquad \text{s.t.} \min y_i(w^T x_i +b) = 1 \Leftrightarrow y_i(w^T x_i + b) \geq 1, i=1, ..., N\]这里的约束是我们令 $\gamma = 1$ 之后才满足的等价关系。
一般我们最优化都找最小, 因此有:
\[\min_{w, b} \frac{1}{2} w^Tw \qquad \text{s.t.} \quad y_i(w^Tx_i + b) \geq 1 \quad \forall i=1, ..., N \Leftrightarrow 1 - y_i(w^Tx_i + b) \leq 0 \quad \forall i=1, ..., N\]$w^Tw$ 与 $\sqrt{w^Tw}$是等价优化的, $\frac{1}{2}$是为了方便计算。
这是一个具有 $n$ 个约束的二次的凸优化问题(convex optimization)
上式是一个 元问题 (primal problem), 我们要找它的对偶问题(dual problem).
构造拉格朗日函数(拉格朗日乘数法是求条件极值的一种方法,具体过程就是将带条件的函数极值问题转化为无条件的极值问题), 将带约束的问题转化为无约束的问题:
\[\mathcal{L}(w, b, \lambda) = \frac{1}{2} w^Tw +\sum_{i=1}^N \lambda_i (1 - y_i(w^Tx_i +b)) \quad \text{s.t. } \lambda_i \geq 0\]Blabla 后面听不懂….
经过 带约束 $\rightarrow$ 无约束 $\rightarrow$ 强对偶关系, 得到:
\[\min_\lambda \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \lambda_i \lambda_j y_i y_j x_i^T x_j - \sum_{i=1}^N \lambda_i \qquad \text{s.t. } \lambda_i \geq 0, \sum_{i=1}^N \lambda_i y_i = 0\]原对偶问题具有强对偶关系 $\Leftrightarrow$ 满足 KTT 条件:
Soft-Margin SVM
核函数变换与支持向量机
线性支持向量机的对偶问题:
\[\max_{\alpha} Q(\alpha) = \sum_{i=1}^N - \frac{1}{2}\alpha_i \alpha_j y_i y_j (x_i · x_j) \qquad \text{s.t. } \sum_{i=1}^N y_i \alpha_i = 0, 0 \leq \alpha_i \leq C, i = 1, ..., N\]判别函数:
\[f(x) = \text{sgn}\{g(x)\} = \text{sgn}\{(w^* · x) + b\} = \text{sgn}\{\sum_{i=1}^N \alpha_i^* y_i (x_i · x) + b^*\}\]支持向量满足等式: $y_i(\sum_{i=1}^n \alpha_i(x_i · x) + b) - 1 = 0$
Q:为什么 $y_i$ 能提出来?
特征 $x$ 进行非线性变换 $z = \phi(x)$
决策函数:
\[f(x) = \text{sgn}(w^{\phi} · z + b) = \text{sgn} (\sum_{i=1}^n \alpha_i y_i (\phi(x_i) · \phi(x)) + b)\]优化问题变成:
\[\max_{\alpha} Q(\alpha) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i, j=1}^n \alpha_i \alpha_j y_i y_j (\phi(x_i) · \phi(x_j)) \qquad \text{s.t. } \sum_{i=1}^n y_i \alpha_i = 0 \quad 0 \leq \alpha_i \leq C, i=1, ..., n\]支持向量满足等式:
\[y_i \left(\sum_{i=1}^n\alpha_i (\phi(x_i) · \phi(x) + b\right) - 1 = 0\]核函数: $K(x_i, x_j) \mathop{=}^{\Delta} (\phi(x_i) · \phi(x_j))$
变换空间里的支持向量机: $f(x) = \text{sgn}(\sum_{i=1}^n \alpha_i y_i K(x_i, x) + b)$
$\alpha$ 是下列优化问题的解:
\[\max_{\alpha} Q(\alpha) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i, j=1}^n \alpha_i \alpha_j y_i y_j K(x_i · x) \qquad \text{s.t. } \sum_{i=1}^n y_i \alpha_i = 0, 0 \leq \alpha_i \leq C, i=1, ..., n\]支持向量满足等式:
\[y_i \left(\sum_{i=1}^n \alpha_i K(x_i · x) + b\right) - 1 = 0\]基于核的的支持向量机
基于核的SVM基本思想:
- 通过非线性变换将输入空间变换到一个高维空间
- 在这个新空间求解最优分类面, 即最大间隔分类面
- 非线性变换通过适当的内积核函数实现
- 求解一个有约束的二次优化问题, 有唯一最优解, 这与多层感知机网络相比是一个优势
- 问题的计算复杂度由样本数目决定, 不取决于样本的特征维数 与 所采用的核函数
三种常见的核函数
多项式核函数:
\[K(x, x') = ((x · x') + 1)^q\]径向基(RBF) 核函数:
\[K(x, x') = \exp(-\frac{(x - x')^2}{\sigma^2})\]Sigmoid 函数:
\[K(x, x') = \tanh(v(x · x') + c)\]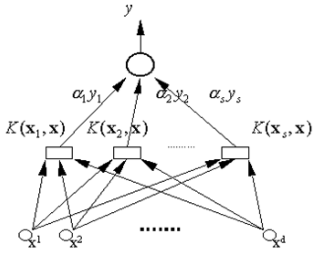
输出(决策规则):
\[y = \text{sgn}(\sum_{i=1}^s \alpha_i y_i K(x_i, x) + b)\]权值 $w_i = \alpha_i y_i$
基于 $s$ 个支持向量 $x_1, x_2, …, x_s$ 的非线性变换(内积)
输入向量 $x = (x^1, x^2, …, x^d)$
非监督学习方法
动态聚类
多次迭代, 逐步调整类别划分, 最终使某准则达到最优
三个要点:
- 选某种距离作为样本相似性度量
- 定义某个准则函数, 用于评价聚类质量
- 初始分类方法及迭代算法
C均值算法
误差平方和聚类准则:
\[J_e = \sum_{i=1}^c \sum_{y \in \Gamma_i} \| y - m_i \|^2 = \sum_{i=1}^c J_i\]其中, $\Gamma_i$ 是第 $i$ 个聚类, $i=1, …, c$, 其中样本数为 $N_i$
$\Gamma_i$ 中的样本均值为 $m_i=\frac{1}{N_i}\sum_{y \in \Gamma_i} y$
直观理解:
- $J_e$ 反映了用 $c$ 个聚类中心代表 $c$ 个样本子集所带来的总的误差平方和
- $J_e$ 是样本集 $\gamma$ 与 类别集 $\Omega$ 的函数。
设已有一个划分方案, 考察 $\Gamma_k$ 中的样本 $y$, 若把 $y$ 移入 $\Gamma_j$, 此时 $\Gamma_k$ 变成 $\tilde \Gamma_k$, $\Gamma_j$ 变成 $\tilde \Gamma_j$, 有:
\[\tilde{m_k} = m_k + \frac{1}{N_k -1}[m_k - y]\] \[\tilde m_j = m_j + \frac{1}{N_j + 1}[y - m_j]\] \[\tilde{J_k} = J_k - \frac{N_k}{N_k - 1} \|y - m_k\|^2\] \[\tilde{J_j} = J_j + \frac{N_j}{N_j + 1} \|y - m_j\|^2\]若 $\frac{N_j}{N_j + 1}|y - m_j|^2 < \frac{N_k}{N_k - 1}|y - m_k|^2$, 则把 $y$ 从 $\Gamma_k$ 移入 $\Gamma_j$ 会使 $J_e$ 减小。
1)初始划分 $c$ 个聚类, $\Gamma_i, i=1, …, c$, 计算 $m_i, i=1, …, c$ 和 $J_e$
2) 选样本 $y$, 设 $y \in \Gamma_i$
3)若 $N_i = 1$, 则 转(2); 否则继续;
4)计算 $\rho_j$:
\[\rho_j = \frac{N_j}{N_j + 1} \| y - m_j \|^2, j \neq i\] \[\rho_i = \frac{N_i}{N_i - 1} \|y - m_i\|^2\]5)选 $\rho_j$ 中的最小者, 即若 $\rho_k < \rho_j$, $\forall j$, 则把 $y$ 从 $\Gamma_i$ 移到 $\Gamma_k$ 中
6) 重新计算 $m_i, i=1, …, c$ 和 $J_e$
7)若连续 $N$ 次迭代 $J_e$ 不改变, 则停止; 否则转 (2)。
深度生成模型
生成对抗网络 是通过对抗训练的方式来使得生成网络产生的样本服从真实数据分布。 在生成对抗网络中,有两个网络进行对抗训练。
判别网络 目标是尽量准确地判断一个样本是来自于真实数据还是生成网络产生的
生成网络 目标是尽量生成判别网络无法区分来源的样本。
这两个目标相反的网络不断地进行交替训练,当最后收敛时, 如果判别网络再也无法判断出一个样本的来源, 那么也就等价于生成网络可以生成符合真实数据分布的样本。
伪代码
输入: 训练集 $D$, 对抗训练迭代次数 $T$, 每次判别网络的训练迭代次数 $K$, 小批量样本数量 $M$
随机初始化 $\theta, \phi$
for t $\leftarrow$ 1 to $T$ do
$\qquad$ for k $\leftarrow$ 1 to $K$ do
$\qquad$ $\qquad$ // 采集小批量训练样本
$\qquad$ $\qquad$ 从训练集 $D$ 中采集 $M$ 个样本 ${x^{(m)}}, 1 \leq m \leq M$
$\qquad$ $\qquad$ 从分布 $N(0, I)$ 中采集 $M$ 个样本 ${z^{(m)}}, 1 \leq m \leq M$
$\qquad$ $\qquad$ 使用随机梯度上升更新 $\phi$, 梯度为:
\[\frac{\partial}{\partial \phi}\left[\frac{1}{M} \sum_{m=1}^M (\log D(x^{(m)}, \phi) + \log(1 - D(G(z^{(m)}, \theta), \phi))\right]\]$\qquad$ end
$\qquad$ // 训练生成网络 $G(z, \theta)$
$\qquad$ 从分布 $N(0, I)$ 中采集 $M$ 个样本 {$z^{(m)}$}, $1 \leq m \leq M$
$\qquad$ 使用随机梯度上升更新 $\theta$, 梯度为:
\[\frac{\partial}{\partial \theta}\left[\frac{1}{M} \sum_{m=1}^M D(G(z^{(m)}, \theta), \phi) \right]\]end
输出: 生成网络 $G(z, \theta)$
深度强化学习
在强化学习中的基本要素包括:
- 状态 $s$ 是对环境的描述, 可以是离散的或连续的, 其状态空间为 $S$
- 动作 $a$ 是对智能体行为的描述, 可以是离散的或连续的, 其动作空间为 $A$
- 策略 $\pi(a \mid s)$ 是智能体根据环境状态 $s$ 来决定下一步的动作 $a$ 的函数
- 状态转移概率 $p(s’ \mid s, a)$ 是在智能体根据当前状态 $s$ 做出一个动作 $a$ 之后, 环境在下一个时刻转变为状态 $s’$ 的概率
- 即时奖励 $r(s, a, s’)$ 是一个标量函数, 即智能体根据当前状态 $s$ 做出动作 $a$ 之后, 环境会反馈给智能体一个奖励, 这个奖励也经常和下一个时刻的状态 $s’$ 有关。
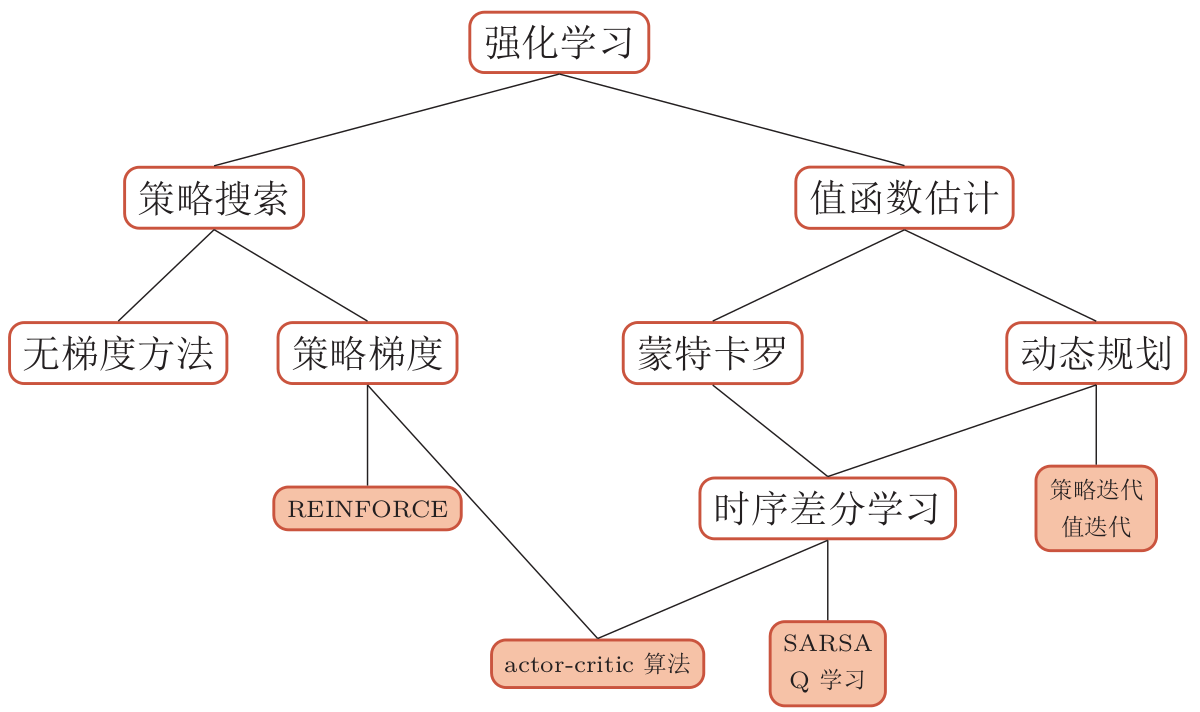
强化学习的算法非常多, 大体上可分为基于 值函数 的方法(包括动态规划, 时序差分学习等)、 基于策略函数 的方法(包括策略梯度等)以及融合两者的方法。 不同算法之间的关系如图所示: