在本节中，我们将讨论优化和深度学习之间的关系，以及在深度学习中优化的挑战。对于深度学习问题，我们通常会先定义一个 损失函数。一旦我们有了损失函数，我们就可以使用优化算法来尝试最小化损失。在优化中，损失函数常被称为优化问题的目标函数。根据传统和惯例，大多数优化算法都是关于 最小化 的。如果我们需要最大化一个目标，有一个简单的解决方案: 翻转目标函数的符号。

Goal of Optimization

虽然优化为深度学习提供了一种最小化损失函数的方法，但从本质上讲，优化的目标与深度学习的目标是完全不同的。前者主要关注最小化一个目标，而后者关注在给定有限数据的情况下找到一个合适的模型。在第4.4节中，我们详细讨论了这两个目标之间的区别。例如，训练误差和泛化误差一般是不同的: 由于优化算法的目标函数通常是基于训练数据集的损失函数，优化的目标是减少训练误差。然而，深度学习(或者更广义地说，统计推理)的目标是减少泛化误差。为了实现后者，除了使用优化算法减少训练误差外，还需要注意过拟合。

%matplotlib inline
import numpy as np
import torch
from mpl_toolkits import mplot3d
from d2l import torch as d2l

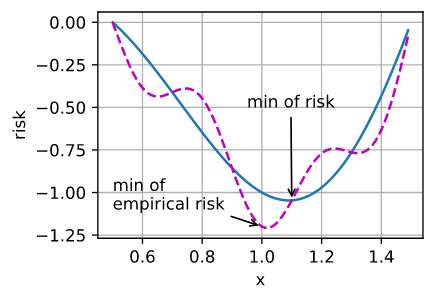
为了说明上述不同的目标，让我们考虑经验风险和风险。如4.9.3.1节所述，经验风险是训练数据集上的平均损失，而风险是整个数据集上的期望损失。下面我们定义了两个函数:风险函数 $f$ 和经验风险函数 $g$。假设我们只有有限数量的训练数据。$f$ 比 $g$ 曲线更加光滑一些。

def f(x):
    return x * torch.cos(np.pi * x)

def g(x):
    return f(x) + 0.2 * torch.cos(5 * np.pi * x)

下图说明了训练数据集上经验风险的最小值可能与风险的最小值(泛化误差)处于不同的位置。

def annotate(text, xy, xytext):  #@save
    d2l.plt.gca().annotate(text, xy=xy, xytext=xytext,
                           arrowprops=dict(arrowstyle='->'))

x = torch.arange(0.5, 1.5, 0.01)
d2l.set_figsize((4.5, 2.5))
d2l.plot(x, [f(x), g(x)], 'x', 'risk')
annotate('min of\nempirical risk', (1.0, -1.2), (0.5, -1.1))
annotate('min of risk', (1.1, -1.05), (0.95, -0.5))

Optimization Challenges in Deep Learning

在本章中，我们将特别关注优化算法在最小化目标函数时的性能，而不是模型的泛化误差。在3.1节中，我们区分了优化问题中的解析解和数值解。在深度学习中，大多数目标函数都是复杂的，没有解析解。进而，我们必须使用数值优化算法。本章的优化算法都属于这一类。

深度学习优化存在诸多挑战。一些最令人烦恼的问题是局部极小值、鞍点和梯度消失。

Local Minima

对于任意的目标函数 $f(x)$，如果在 $x$ 处 $f(x)$ 的值小于 $x$ 附近其他点的 $f(x)$ 的值，那么 $f(x)$ 就可能是一个局部最小值。如果在 $x$ 点处 $f(x)$ 的值在整个定义域上都是目标函数的最小值，那么 $f(x)$ 是全局最优解。

例如，给定函数：

\[f(x) = x \cos(\pi x) \text{ for -1.0} \leq x \leq 2.0\]

我们可以估计这个函数的局部最小值和全局最小值。

x = torch.arange(-1.0, 2.0, 0.01)
d2l.plot(x, [f(x),], 'x', 'f(x)')
annotate('local minimum', (-0.3, -0.25), (-0.77, -1.0))
annotate('global minimum', (1.1, -0.95), (0.6, 0.8))

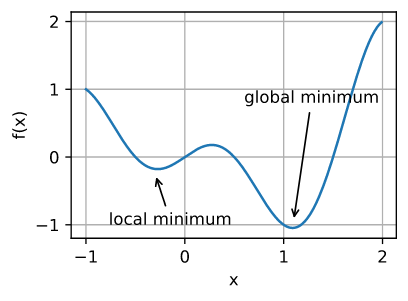
深度学习模型的目标函数通常有许多局部最优值。当优化问题的数值解接近局部最优时，目标函数解的梯度趋近或为零，最终迭代得到的数值解只能使目标函数的局部最小，而不能使目标函数的全局最小。只有某种程度的噪声才能使参数脱离局部最小值。事实上，这是小批量随机梯度下降的一个有益性质，在小批量上梯度的自然变化可以使参数跳出局部极小值。

Saddle Points

除了局部极小值，鞍点是梯度消失的另一个原因。鞍点是一个函数的所有梯度都消失但既不是全局最小值也不是局部最小值。例如函数 $f(x) = x^3$。它的一阶导数和二阶导数在 $x=0$ 时为零。此时即使它不是最小值，优化也可能会停止。

x = torch.arange(-2.0, 2.0, 0.01)
d2l.plot(x, [x**3], 'x', 'f(x)')
annotate('saddle point', (0, -0.2), (-0.52, -5.0))

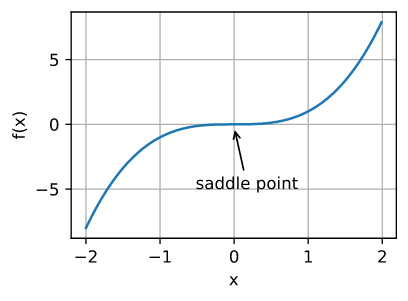
在更高维度中，鞍点更加隐蔽，如下面的示例所示。如函数 $f(x, y) = x^2 - y^2$。它在 $(0, 0)$ 点为鞍点。

x, y = torch.meshgrid(torch.linspace(-1.0, 1.0, 101),
                      torch.linspace(-1.0, 1.0, 101))
z = x**2 - y**2

ax = d2l.plt.figure().add_subplot(111, projection='3d')
ax.plot_wireframe(x, y, z, **{'rstride': 10, 'cstride': 10})
ax.plot([0], [0], [0], 'rx')
ticks = [-1, 0, 1]
d2l.plt.xticks(ticks)
d2l.plt.yticks(ticks)
ax.set_zticks(ticks)
d2l.plt.xlabel('x')
d2l.plt.ylabel('y');

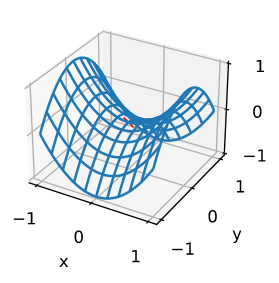
我们假设函数的输入是一个 $k$ 维向量并且它的输出是一个标量，它的海森矩阵将会有 $k$ 个奇异值。函数梯度为零时的解可能为一个局部最小值，局部最大值，或者一个鞍点：

当函数的Hessian矩阵在零梯度位置的特征值都为正时，我们得到了函数的局部最小值。
当函数的Hessian矩阵在零梯度位置的特征值都为负时，函数有一个局部极大值。
当函数的Hessian矩阵在零梯度位置的特征值有正有负时，我们得到了函数的鞍点。

对于高维问题，某些特征值是负的可能性是相当高的。这使得鞍点比局部极小点更有可能出现。我们将在下一节介绍凸性时讨论这种情况的一些例外情况。简而言之，凸函数是那些海森函数的特征值都不为负的函数。遗憾的是，大多数深度学习问题都不属于这一类。尽管如此，它还是研究优化算法的一个很好的工具。

Vanishing Gradients

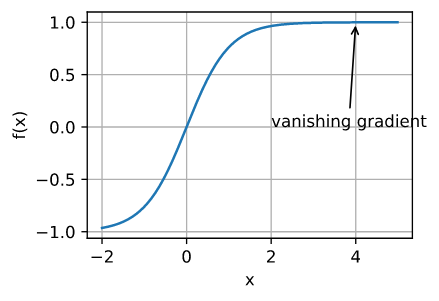
可能遇到最棘手的问题是梯度消失。回顾我们在第4.1.2节中常用的激活函数及其导数。例如，假设我们想要最小化函数 $f(x) = tanh(x)$ , 我们从4开始。我们可以看到， $f$ 的梯度接近于0。特别地， $f’(x) = 1 - tanh^2(x)$ 且 $f’(4) = 0.0013$。因此，在我们取得进展之前，优化会被卡住很长一段时间。这就是为什么在引入ReLU激活函数之前，训练深度学习模型非常棘手的原因之一。

x = torch.arange(-2.0, 5.0, 0.01)
d2l.plot(x, [torch.tanh(x)], 'x', 'f(x)')
annotate('vanishing gradient', (4, 1), (2, 0.0))

正如我们所看到的，深度学习的优化充满了挑战。幸运的是，现在已经有了一系列性能良好且即使是初学者也很容易使用的算法。此外，并不真的需要找到全局最优解。局部最优解甚至近似解也是非常有用的。

Summary

使训练误差最小化并不能保证我们找到最优的参数集来最小化泛化误差。
优化问题可能有许多局部极小值。
优化问题可能有更多的鞍点，因为一般情况下优化问题不是凸的。
梯度消失会导致优化失速。通常重参数化问题会有所帮助。良好的参数初始化也是有益的。

Exercises

考虑一个单隐藏层的多层感知机，也就是说，隐藏层有 $d$ 个维度并且有单个输出。表明任意局部最小值至少有 d 个表现完全等价的解。
假设我们有一个对称随机矩阵 $M$，其中 $M_{ij} = M_{ji}$, 每个值从概率分布 $p_{ij}$ 采样。进一步假设 $p_{ij}(x) = p_{ij}(-x)$，这个分布就是对称的。
- 证明特征值上的分布也是对称的。也就是说，对于任意的奇异向量 $v$ ，相应的奇异值 $\lambda$ 的概率满足 $P(\lambda > 0) = P(\lambda < 0)$。
- 为什么上面没有表明 $P(\lambda > 0) = 0.5$？
你能想到深度学习优化的其他挑战吗？
假设你想要把一个球放在一个鞍点保持平衡
- 为什么困难？
- 你能利用这个效应来优化算法吗？

【d2l】Optimization and Deep Learning