Adagrad

Sparse Features and Learning Rates

假设我们正在训练一个语言模型。为了获得良好的准确率，我们通常希望在继续训练的同时降低学习率， 通常为 $O(t^{-\frac{1}{2}})$ 或者更慢。 现在考虑一个基于稀疏特征的模型训练，即只出现很少的特征。这在自然语言处理中很常见， 相比于 learning， 我们更多地见到 preconditioning。 稀疏特征也在广告推荐和个性化定制中也很常见。 毕竟，有许多事情只有少数人感兴趣。

与稀疏特性相关的参数只有在这些特征出现时才会得到有意义的更新。如果学习率降低，我们可能会陷入这样一种情况: 常见特征的参数会很快收敛到它们的最优值，而对于不常见特征，在确定它们的最优值之前，我们缺乏仍然观测到它们的次数。换句话说，对于出现频繁的特征，学习率下降得太慢，对于出现不频繁的特征，学习率下降得太快。

解决这个问题的一种可能的方法是计算我们看到一个特定特征的次数，并将其用作调整学习速率的时钟。也就是说， 与其选择一个 $\eta = \frac{\eta_0}{\sqrt{t + c}}$ 形式的学习率， 我们可以使用 $\eta_i = \frac{\eta_0}{\sqrt{s(i, t) + c}}$。 这里， $s(i, t)$ 计算观测到特征 $i$ 的次数 $t$ 。

Adagrad 将之前观测到的梯度的平方的累积 替换掉 $s(i, t)$ 。特别地， 它使用 $s(i, t+1) = s(i, t) + (\partial_i f(x))^2$ 调整学习率。 这有两个好处: 首先，我们不再需要决定什么时候梯度足够大。其次，它会随着梯度的大小自动缩放。通常对应大梯度的坐标被显著地按比例缩小， 而其他梯度小的则会得到更温和的处理。在实践中，这位广告推荐和相关问题提供了一个非常有效的优化过程。 但这隐藏了Adagrad内在的一些额外好处，这些好处在 Preconditioning 的背景下可以得到最好的理解。

Preconditioning

凸优化问题有利于分析算法的特点。毕竟，对于大多数非凸问题来说，很难得出有意义的理论保证，但直觉和洞察力往往会延续下去。让我们看一下最小化问题 $f(x) = \frac{1}{2}x^TQx + c^Tx + b$。

可以重写这个问题为它的特征值和特征向量 $Q = U^T \Lambda U$ 来让它变成一个简化的问题， 每个坐标都可以单独地处理：

这里， $x = Ux$ 并且 $c = Uc$。 修改后的问题有极值点 $\bar x = -\Lambda^{-1} \bar c$ 以及 极值 $-\frac{1}{2} \bar c^T \Lambda \bar c + b$。 $\Lambda$ 是对角线为特征值 Q 的对角矩阵， 因此更容易计算。

如果我们轻微扰动 $c$， 我们希望找到 $f$ 的极值点的轻微变化。 尽管 $c$ 的微小变化导致 等价的 $\bar c$ 的微小变化， …?。 当特征值 $\Lambda_i$ 很大， 我们将会看到 $x_i$ 很小的变化以及 $\bar f$ 的最小值。 相反， 对于在 $\bar x_i$ 中的 小的 $\Lambda_i$ 变化非常剧烈。 最大特征值与最小特征值之比称为优化问题的条件数。

如果条件数大， 精确求解优化问题是一项困难的工作。我们需要确保在正确地获得一个大的动态范围的值时非常谨慎。我们的分析引出了一个明显的、尽管有些幼稚的问题： 为什么不直接固定这个问题， 通过变换空间使得所有特征值为1. 理论上来讲这是容易的， 我们仅需要特征值和特征向量 $Q$ 来将 $x$ 缩放为 $z$： $z := \Lambda^{\frac{1}{2}} U x$。 在新的坐标系统 $x^TQx$ 可以被简化为 $|z|^2$。 计算特征值和特征向量通常比解决实际问题要昂贵得多。

虽然准确地计算特征值可能是昂贵的，在某种程度上猜测它们和计算它们可能比什么都不做要好得多。特别地， 我们可以使用 $Q$ 的对角阵， 并且根据它进行缩放。 这笔计算特征值容易得多。

这里， 对于所有 $i$， 我们有$\tilde Q_{ij} = Q_{ij} / \sqrt{Q_{ii}Q_{jj}}$ ， 并且特别地 $\tilde Q_{ii} = 1$。 在大多数情况下，这大大简化了条件数。例如，在我们前面讨论的案例中，这将完全消除之前的问题，因为这个问题是轴对齐的。

不幸的是，我们还面临着另一个问题: 在深度学习中，我们通常甚至不能得到目标函数的二阶导数： 对于 $x \in \mathbb{R}^d$， 在一个 minibatch 上的二阶导数可能需要 $O(d^2)$ 的空间取计算。 Adagrad的巧妙想法是使用一个代理——梯度本身的规模, 来代替难以找到的Hessian 对角矩阵，它的计算相对便宜和并且很有效 。

为了看它为什么起作用， 我们来看 $\bar f(\bar x)$。 我们有：

这里 $\bar x_0$ 是 $\bar f$ 的极小值点。 因此梯度的规模同时依赖于 $\Lambda$ 和 离最优解的距离。 如果 $\bar x - \bar x_0$ 不变， 这将是所有所需要的。 由于AdaGrad是一种随机梯度下降算法，即使在最优解下，我们也会看到方差非零的梯度。因此，我们可以安全地使用梯度的方差作为Hessian尺度的代理。

The Algorithm

我们用变量 $s_t$ 按一下的方式累计过去的梯度方差：

这里的操作应用在每个坐标上。 $\eta$ 是学习率， $\epsilon$ 确保分母不为0。 最后， 我们初始化 $s_0 = 0$

就像在动量的情况下，我们需要跟踪一个辅助变量，在这种情况下，允许每个坐标的单独学习速率。相对于SGD, Adagrad的成本并没有显著增加， 主要的成本在计算 $l(y_t, f(x_t, w))$ 以及它的偏导。

注意在 $s_t$ 中的累计平方梯度 意味着 $s_t$ 以线性增长。 这将导致 $O(t^{-\frac{1}{2}})$ 的学习率， 尽管在每一个坐标点调整。 对于凸问题，这是完全充分的。 然而，在深度学习中，我们可能想要更慢地降低学习率。这导致了许多Adagrad变体，我们将在随后的章节中讨论。现在让我们看看它在二次凸问题中的表现。我们使用和之前相同的问题：

我们使用和之前相同的学习率来实现 Adagrad， 比如 $\eta = 0.4$。 可以看出，自变量的迭代轨迹更加平滑。然而， 由于 $s_t$ 累积的影响， 学习率持续地下降， 因此，自变量在迭代的后期阶段不会移动太多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
%matplotlib inline
import math
import torch
from d2l import torch as d2l


def adagrad_2d(x1, x2, s1, s2):
    eps = 1e-6
    g1, g2 = 0.2 * x1, 4 * x2
    s1 += g1**2
    s2 += g2**2
    x1 -= eta / math.sqrt(s1 + eps) * g1
    x2 -= eta / math.sqrt(s2 + eps) * g2
    return x1, x2, s1, s2

def f_2d(x1, x2):
    return 0.1 * x1**2 + 2 * x2**2

eta = 0.4
d2l.show_trace_2d(f_2d, d2l.train_2d(adagrad_2d))

1
epoch 20, x1: -2.382563, x2: -0.158591

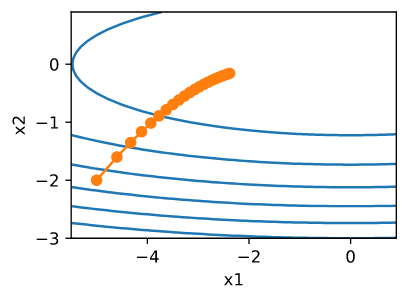
当我们把学习速率提高到 2 时，我们会看到更好的表现。这已经表明，即使在无噪声的情况下，学习率的下降可能是相当严重的，我们需要确保参数适当地收敛。

• Previous
  【d2l】Momentum
• Next
  【d2l】RMSProp