机器学习涉及控制概率。 这些概率通常表示为 normalised-probabilities 或 log-probabilities。掌握这两种表示之间灵活转换的能力是增强我们解决现代机器学习问题的关键一步。log derivative trick 利用对数导数的性质帮助我们。这个技巧在我们用它来解决随机优化问题时很有用,它将给我们提供一种新的方法来推导随机梯度估计量。我们首先来定义一个 score 函数。
Score Functions
log derivative trick 是关于函数 $p(x; \theta)$ 的对数 对 参数 $\theta$ 的梯度法则的应用:
这个技巧的重要性是在函数 $p(x; \theta)$ 是似然函数时体现的。 在这个例子下, 函数 $\nabla_\theta \log p(x; \theta)$ 叫做 score function, 而右侧是 score ratio。 score function 有大量有用的性质:
- 最大似然估计的 central computation。
- score 的期望值是 0。
在第一行我们使用了 log derivative trick, 在第二行我们交换了求导和积分的顺序。 这个恒等式是我们追求的概率灵活性: 它允许我们从 score 中减去任何期望为0的项, 并且不影响score的期望。
- score 的方差是 Fisher information 并且 用来决定 Cramer-Rao lower bound。
我们现在可以从对数概率的梯度 变换为 概率的梯度,然后再变换回来。
Score Function Estimators
我们的问题是计算一个函数 $f$ 的期望的梯度:
\[\nabla_\theta \mathbb{E}_{p(z; \theta)}[f(z)] = \nabla_\theta \int p(z; \theta) f(z) dz\]这是机器学习中一个反复出现的任务, 变分推断的后验计算, 强化学习中的值函数和策略学习, computational finance 的 derivative pricing等等。
梯度很难计算, 因为积分通常是未知的并且有参数 $\theta$。 此外, 我们可能当函数 $f$ 是不可微的时候想要计算这个梯度。使用 log derivative trick 以及 score function 的性质, 我们可以用更合理的方法来计算这个梯度:
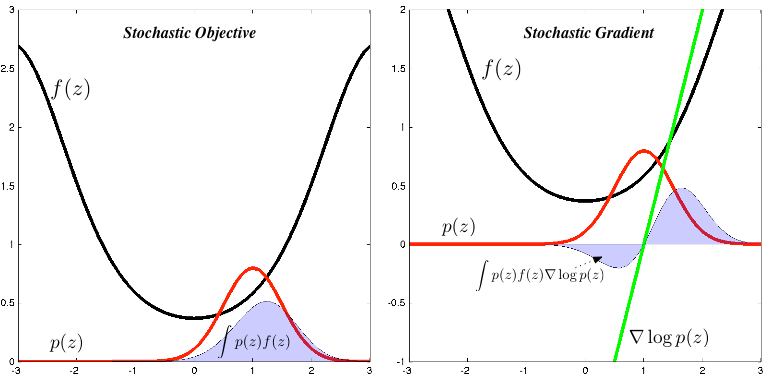
让我们推导这个表达式,并探讨它对优化问题的影响。我们将会使用另外一个十分普遍的技巧 probabilistic identity trick。 结合 probabilistic identity trick 和 log-derivative trick, 我们得到梯度的 score function estimator:
这四行写了很多东西。在第一行,我们交换了导数和积分的顺序。在第二行中, 我们使用了 probabilistic identity trick, 这使得我们得到了 score ratio。 使用 log-derivative trick, 我们使用第三行的对数概率的梯度替换 score ratio 。 第四行就是我们想要的stochastic estimator, 我们从 $p(z)$ 采样通过 Monte Carlo 计算它, 然后计算加权梯度。
这是梯度的 unbiased estimator。 在整个过程中,我们的假设很简单:
- 积分和微分顺序的交换是有效的。 我们可以用
Leibniz integral rule来推理它的正确性。 - $f(z)$ 是不可微的。进而, 给定 $z$ 我们应该能够评估它或者观察到它的值。
- 从分布 $p(z)$ 采样很容易, 因为积分的 Monte Carlo evaluation 所需要的。
其他很多领域的研究已经研究过 log-derivative trick, 并给出了和他们的问题表述相关的名字, 包括:
Score function estimators:我们的微分允许我们将期望的梯度转换为 score function $\nabla_\theta \log p(z ; \theta)$ 的期望, 使得很自然地得到 score function estimators。基于 score function estimators 的计算机仿真模型的优化和敏感度分析 具有非常深刻的见解并且描述了许多重要的历史发展。
Likelihood ratio methods:P. W. Glynn 是在推广这类估计中最有影响力的人之一。Glynn 把 score ratio $\nabla_\theta p(z; \theta) / p(z; \theta)$ 解释为 likelihood ratio, 并且描述这个 estimators 为 likelihood ratio 方法。重要的paper:
- ‘Likelihood Ratio Gradient Estimation for Stochastic Systems’, Glynn 详细解释了重要的方差性质。
- Gradient Estimation by Michael Fu is indispensable。
Automated Variational Inference:变分推断将贝叶斯分析中出现的棘手的积分转化为随机优化问题。毫无意外, score function estimators 也出现在这个领域, 并且有很多不同的名字: variational stochastic search, automated variational inference, black-box variational inference 和 neural variational inference 等。
REINFORCE and policy gradients: 对于强化学习问题, 我们可以将函数 $f$ 映射为 从环境中获得的 reward, 分布 $p(z; \theta)$ 为 policy, 以及 score 为 policy gradient。 一种直观的解释如下: policy 的任意梯度对应于更高 rewards 有更高的权重-reinforced-通过 estimator。 因此, estimator 被叫做 REINFORCE, 它的推广现在是 policy gradient theorem 形式。
Control Variates
为了使 Monte Carlo estimator 有效, 我们必须确保方差尽可能地小——否则梯度就没有用了。为了更好地控制方差,我们使用改进的estimator:
\[\nabla_\theta \mathbb{E}_{p(z;\theta)}[f(z)] = \mathbb{E}_{p(z;\theta)}[f(z) - \lambda \nabla_\theta \log p(z; \theta)]\]其中 $\lambda$ 叫做 control variate, 在 Monte Carlo estimators 中被广泛用于减小方差。control variate 可以是任意使得 estimator 均值为 0 的项。 control variate 的选择是在使用 score function estimators 的主要挑战。最简单的方法是使用一个常数baseline, 但是也有其他方法被使用, 比如 clever sampling schemes (例如 antithetic 或stratified), delta methods, 或者自适应 baseline。
Summary
` log derivative trick` 使我们可以在 normalised probability 和 log-probability 分布表示之间转换。它是 score function 的基础, 并且使最大似然估计成为可能。 重要的是,我们可以利用它为随机优化问题提供一个通用 gradient estimator,而随机优化问题是我们目前面临的许多最重要的机器学习问题的基础。 我们追求的通用机器学习需要 Monte Carlo gradient estimators, 理解它们以及建立在它们之上的tricks是必要的。
Reference
Machine Learning Trick of the Day (5): Log Derivative Trick