Abstract
DeepSC 的目的是最大化系统容量 并且 最小化语义误差, 而不是传统通信中比特或者符号级的误差。
迁移学习用于 DeepSC 在不同通信环境中的应用 以及 加速模型的训练。
为了准确地验证语义通信的性能, 提出一种叫做句子相似度的指标。
Introduction
通信系统的三个层次:1)符号的传输 2)传输符号中的语义 3) 由语义信息传输所带来的影响
通信的第一个层次主要关注于发送器到接收器的符号传输的成功率, 它的准确率主要在比特或者符号级上。
通信的第二个层级处理发送方发送的语义信息 以及 接收方接收的含义, 叫做语义通信。
通信的第三个层级处理通信的影响, 即转变为接收方执行发送方特定任务的意图。
问题:自动交通、消费机器人、环境监测和远程健康等 这些应用需要在有限的频谱资源上支持大量的连接, 并且需要更低的延迟, 这给传统信源信道编码带来了关键的挑战。
语义通信通过在语义域上提取出数据的含义以及滤除无用的、无关的、不必要的信息处理数据, 可以在保留含义的基础上进一步地压缩数据。
语义通信在糟糕的信道上, 比如低信噪比的信道上有更强的鲁棒性。
语义通信与传统通信不同的的地方在于语义通信的目标是传输和通信目的相关的信息。
语义通信发展史:
- Carnap 等人基于逻辑概率第一次引入语义信息论。
- 作为语义信息论的拓展, 语义通信的通用模型(GMSC)被提出, 其中语义噪声和语义信道的概念首次被定义。
- 用于 GMSC 的语义数据压缩理论的损失函数被提出, 这意味着数据可以在语义级被压缩, 因此要传输数据的大小可以被显著地减小。
- 最近, 一个整合了语义推理和物理层通信问题的端到端的语义通信框架被提出, 它的transceiver 被优化达到纳什均衡的同时最小化平均语义误差。
然而它的语义误差的测量是在次级别的而不是在句子级别。
这篇文章所提出的语义通信系统主要关注于联合语义-信道编码和解码, 其目标是提取和编码句子的语义信息, 而不只是比特序列或者一个单词。
语义通信系统将面临以下问题:
- 如何定义比特背后的含义?
- 如何测量句子的语义误差?
- 如何联合设计语义和信道的编码?
这篇文章的主要贡献总结如下:
- 基于Transformer, 提出一个新的 DeepSC 框架, 它能够从文本中有效地提取语义信息, 并且对噪声有强鲁棒性。所提出的DeepSC, 联合 语义-信道 编码 用以处理通道噪声和语义变形, 解决上面的问题3.
- DeepSC 的 transceiver 由语义编码器, 信道编码器, 信道解码器 和 语义解码器组成。为了理解语义含义的同时最大化系统容量,接收器优化两个损失函数: 交叉熵和互信息。 此外, 还提出一个新的指标反映 DeepSC 在语义级别的表现。 这些解决了问题1和问题2.
- 为了使 DeepSC 在各种通信场景下可用, 深度迁移学习用于模型的再训练。 有了再训练的模型, DeepSC可以识别不同的知识输入和恢复变形的语义信息。
- 基于实验发现, DeepSC在低信噪比环境下比传统通信系统表现更好。
Related Work
End-to-End Physical Layer Communication Systems
根据BER, 端到端(E2E)的系统比BPSK(binary phase shift keying) 和 海明编码的 BPSK 表现更好。
在训练期间处理缺失信道梯度,一个基于两阶段训练的DNN被提出, 一个transceiver用一个随机信道模型训练, 一个 receiver 在真实信道下微调。
利用强化学习来获取未知信道模型下的信道梯度,其性能在真实信道上优于differential quadrature phase-shift keying(DQPSK)。
条件生成对抗网络使用 DNN 表征信道失真, 以便在端到端通信系统的训练过程中梯度通过未知信道到达 transmitter DNN。
元学习被用于训练 transceiver 并且 使得在仅有少量数据的情况下快速训练网络。
根据源信息的类型, 对文本和图像进行 source-channel 联合编码的目的是直接在 receiver 恢复源信息, 而不是比特。
传统如 BER 的指标不能很好地反映这种系统的性能。 因此,采用 word-error rate 和 峰值信噪比 (PSNR) 测量源信息恢复的准确率。
Semantic Representation in Natural Language Processing
- 根据上下文建立的联合概率模型
- word2vec
- BERT
Comparison of State-of-Art NLP Techniques
对于主语和谓语距离超过10个词的句子, RNN无法找到正确的主语和谓语。
RNN 并行性不好。
为了保证计算效率, CNN的kernel size 很小, 这导致它的表现不如 RNN。
Transformer 同时具有 RNN 和 CNN 的优势。
SYSTEM MODEL AND PROBLEM FORMULATION
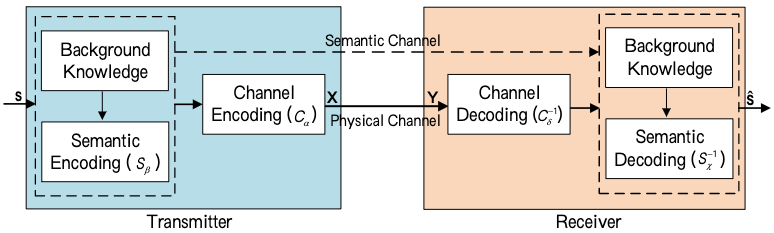
考虑的系统包含两层: 语义层和传输层。
语义层处理语义信息, 通过编码和解码提取语义信息。
传输层保证语义信息在 transmission medium 上正确传输。
智能端到端通信系统采用随机物理信道, transceiver 和 receiver 具有不同的背景知识, 即不同的训练数据。背景知识对不同应用场景不同。
定义一: 语义噪声是信息传输中的一种干扰, 其由于在信息传输中使用的词语、句子或符号的歧义而妨碍信息的解释。
定义二: 物理信道噪声是有物理信道损坏引起的, 例如 , 加性高斯白噪声(AWGN), 信道衰落以及多径, 这会导致信号衰减和失真。
Problem Description
transmitter 将句子 $s$ 映射为复杂的符号流 $x$, 然后通过带有 transmission 损坏的物理信道, 比如失真和噪声。 对接收到的 $y$, 在 receiver 被解码用以评估原始的句子 $s$。
使用 DNN 联合设计 transmitter 和 receiver, 因为 DL 使得我们可以使用 可变长的句子和不同的语言来训练一个模型。
假设 DeepSC 的输入 $s = [w_1, w_2, …, w_L]$, 其中 $w_l$ 表示句子中的第 $l$ 个词。transmitter 包括两个部分, 叫做语义编码器和信道编码器, 用以从 $s$ 中提取语义信息 以及 保证在物理信道上成功传输语义信息。 编码符号流可以表示为:
\[x = C_{\alpha} (S_{\beta}(s))\]其中 $x \in \mathbb{C}^{M \times 1}$, $S_{\beta}(·)$ 是参数为 $\beta$ 的语义编码器网络, $C_{\alpha}$ 是参数为 $\alpha$ 信道编码器。
为了简化分析, 我们假设相干时间为 $M$。 如果 $x$ 被发送, receiver 接收到的信号为 :
\[y = hx + n\]其中 $y \in C^{M \times 1}$, $h$ 表示 参数为 $\mathcal{C}\mathcal{N}(0, 1)$ 和 $n \thicksim \mathcal{C}\mathcal{N}(0, \sigma_n^2)$ 的 Rayleigh 衰落信道。
可以用简单的神经网络建模 AWGN 信道, multiplicative Gaussion noise 信道 以及 erasure 信道。对于信道衰落, 需要使用更复杂的神经网络。
这篇文章主要考虑了 AWGN 信道 和 Rayleigh 衰落信道, 重点研究了语义编码和解码。
receiver 包含信道解码器和语义解码器分别用以恢复传输的符号以及传输的句子。解码信号可以表示为:
\[\hat s = S_{\mathcal{X}}^{-1}(C_\delta^{-1}(y))\]系统的目标是最小化语义误差 并且 减少要传输的符号。
该系统存在两个挑战:
- 第一个挑战是如何设计联合 语义-信道编码。
- 第二个是语义传输, 这在传统系统中没有被考虑到
即便现在信道的误码率很低, 但是由于信道的噪声等导致比特上的错误也会导致语义的错误。 使用DNN网络将信道噪声也加入编码过程, 使得DNN具有去噪抗干扰的能力。
使用交叉熵度量 $s$ 和 $\hat s$ 之间的差异:
\[L_{CE}(s, \hat s, \alpha, \beta, \mathcal{x}, \delta) = -\sum_{l=1} q(w_l) \log (p(w_l)) + (1 - q(w_l)) \log (1 - p(w_l))\]其中 $q(w_l)$ 是第 $l$ 个词的真实概率, $p(w_l)$ 是第 $l$ 个词预测概率。通过减小交叉熵, 网络学习到词的概率分布, 它表示语法、段落以及上下文词的含义。联合设计和训练 语义-信道编码使得整个网络对特定的目标学习知识。
Channel Encoder and Decoder Design
互信息可以在训练 receiver 时提供额外的信息
\[I(x; y) = \int_{\mathcal{X} \times \mathcal{Y}} p(x, y) \log \frac{p(x, y)}{p(x)p(y)}dxdy = \mathbb{E}_{p(x, y)}\left[\log \frac{p(x, y)}{p(y)p(x)}\right]\]$p(x)$ 和 $p(y)$ 分别是发送 $x$ 和 接收 $y$ 的边缘概率。互信息等价于边缘概率和联合概率的 KL 散度:
\[I(x; y) = D_{KL}(p(x, y) \| p(x)p(y))\]定理 1:
\[D_{KL}(P \| Q) = \sup_{T: \Omega \rightarrow R} E_P[T] - \log (E_Q [e^T])\]根据定理 1, 可得到:
\[D_{KL}(p(x, y) \| p(x)p(y)) \geq E_{p(x, y)}[T] - \log (E_{p(x)p(y)}[e^T])\]因此可以得到 $I(x; y)$ 的下限。 为了找到 $I(x; y)$ 的下限, 训练一个网络 $T$ 来估计这个下限。
可以通过最大化互信息来优化编码器, 其损失函数如下:
\[L_{MI}(x, y; T) = E_{p(x, y)}[f_T] - \log (\mathbb{E}_{p(x)p(y)}[e^{f_T}])\]其中 $f_T$ 是一个神经网络, 它的输入从 $p(x, y)$, $p(x)$ 和 $p(y)$ 中采样。在这篇文章的设计中, $x$ 由函数 $C_\alpga$ 和 $S_{\beta}$ 生成, 因此损失函数可以通过 $L_{MI}(x, y; T, \alpha, \beta)$ 表示:
\[L_{MI}(x, y; T, \alpha, \beta) \leq I(x; y)\]使用上式的损失函数训练神经网络得到 $\alpha$, $\beta$ 和 $T$。 举个例子, 当编码器的 $\alpha$ 和 $\beta$ 固定的时候, 可以通过训练网络 $T$ 来估计互信息。 当互信息得到之后,可以通过训练 $\alpha$ 和 $\beta$ 优化 encoder。
Performance Metrics
BER 忽略通信的目标。
BLEU 在语义相同时也很难到达 1。
因此提出 句子相似度 指标:
\[\text{match}(\hat s, s) = \frac{B_\Phi(s) · B_\Phi(\hat s)^T}{\|B_\Phi(s)\|\|B_\Phi(\hat s)\|}\]$B_\Phi$ 表示 BERT, 得到的即为 BERT 的表征。将传输的句子和恢复的句子输入 BERT 得到表征向量, 对向量计算余弦相似度。
PROPOSED DEEP SEMANTIC COMMUNICATION SYSTEMS
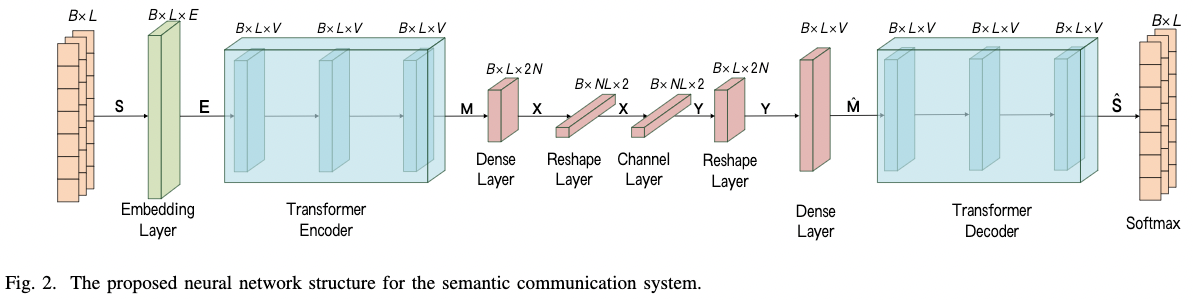
Basic Model
transmitter 包括一个语义编码器从文本中提取语义特征 以及 一个信道编码器 生成符号方便后面的传输。
AWGN 信道在模型中被解释为一层。
receiver 包括一个语义解码器 和 一个信道解码器。
损失函数可以解释为:
\[\mathcal{L}_{total} = \mathcal{L}_{CE}(s, \hat s; \alpha, \beta, \mathcal{X}, \delta) - \lambda L_{MI}(x, y; T, \alpha, \beta)\]注意力机制能够学习语义, 解决问题1。
由于不同的损失函数, DeepSC 的训练包含两个阶段。
第一个阶段通过无监督学习训练互信息模型, 为第二阶段估计 achieved data rate。
联合语义-信道编码解决问题3。
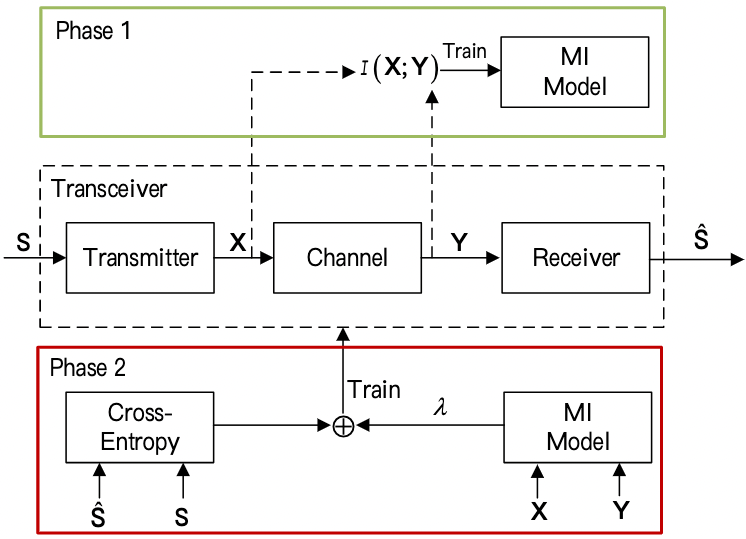
Training of mutual information estimation model:
- 首先, 知识集合 $\mathcal{K}$ 生成一个小批量句子 $S \in \mathcal{R}^{B \times L \times 1}$。
- 经过 Embedding 层, 句子可以表示为词向量 $E \in mathcal{R}^{B \times L \times E}$。
- 然后, 输入语义编码器层得到 $M \in \mathcal{R}^{B \times L \times V}$。
- 然后, $M$ 被编码为符号 $X$ 来处理物理信道的影响, $X \in \mathcal{R}^{B \times NL \times 2}$。
- 传输通过信道后, receiver 得到由信道噪声导致的失真信号 Y。
- 在 AWGN 信道下, 根据发送符号 $X$, 和接收的符号 $Y$, 可以计算损失 $L_{MI}(X, Y; T, \alpha, \beta)$。
- 最后, 根据计算得到的 $L_{MI}$, 使用随机梯度下降优化 $f_T(·)$ 的权重和偏差。
Whole network training:
- 首先, 从知识 $mathcal{K}$ 中采样小批量 $S$, 然后将它编码为语义层级的 $M$, 然后 $M$ 编码为用于在物理信道上传输的符号 $X$。
- 在receiver, 接收到失真符号 $Y$ , 然后被信道解码器层解码为 $\hat M \in \mathcal{R}^{B \times L \times V}$ , 其表示恢复的源信息的语义信息。
- 之后, 语义解码器层预测传输的句子。
- 最后, 整个网络通过SGD优化。
Transfer Learning for Dynamic Environment
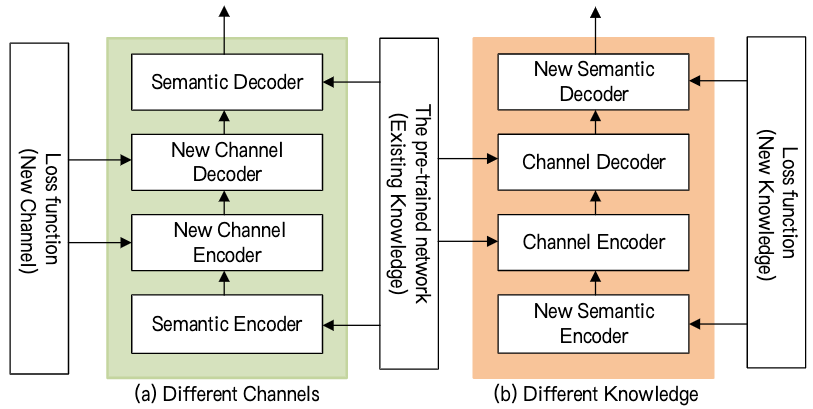
不同通信场景导致不同的信道和训练数据。 为了解决这个问题, 采用深度迁移学习, 专注于存储在解决问题得到的知识, 同时将其应用在不同但相关的问题上。
- 首先, 基于知识 $\mathcal{K}_0$ 和 信道 $\mathcal{N}_0$ 加载预训练的 transmitter 和 receiver。
- 对于不同背景知识的应用, 我们仅需重新设计和训练语义编码器和解码器层, 冻结信道编码器和解码器层。
- 对于不同的通信环境, 我们重新设计和训练信道编码器和解码器层的部分, 冻结语义编码器和解码器层。
NUMERICAL RESULTS
Simulation Settings
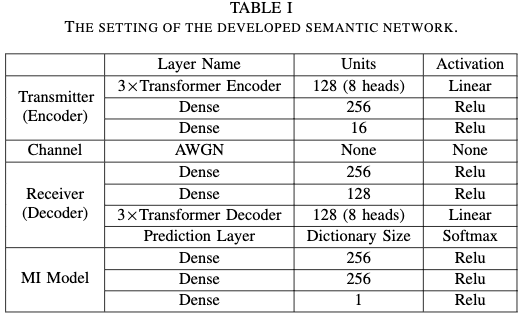
对于baseline, 采用基于神经网络的信源信道编码 以及 典型的信源和信道编码分开的典型方法:
- 基于DNN的信源信道编码: 使用双向LSTM网络(BLSTM)。 将它标记为 JSCC。
- 传统方法:
-
- 信源编码: 哈弗曼编码, 定长编码(5-bit), Brotli编码, 其中 Brotli 编码使用 2nd 上下文模型压缩上下文信息 并且在仿真中 128 个句子被压缩在一起。
-
- 信道编码: Turbo 编码 和 ReedSolomon (RS) 编码。 采用的 turbo 解码方式是5次迭代的 log-MAP 算法。
使用 BLEU 和 句子相似度度量性能。
Basic Model
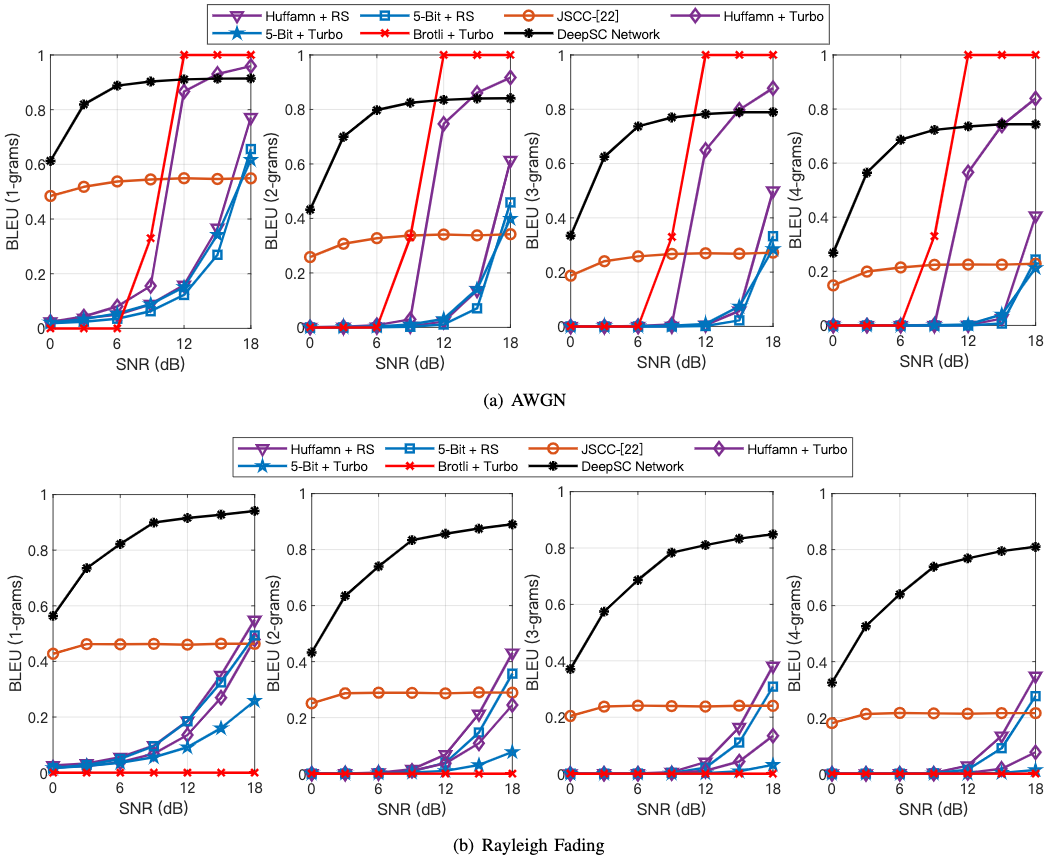
所有DL方法在低信噪比下更具竞争力。
DL 方法在锐利衰减信道上表现比所有传统方法更好。
Mutual Information
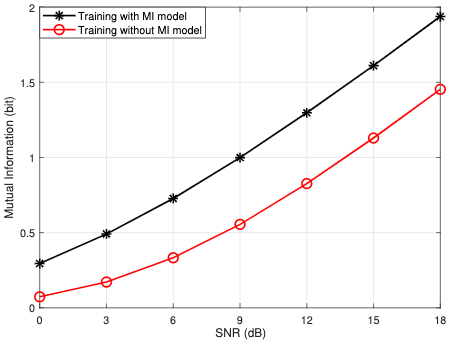
Transfer Learning for Dynamic Environment
Complexity Analysis
Conclusion
提出一种叫作 DeepSC 的语义通信系统, 它为文本传输联合执行 semantic-channel 编码。
DeepSC的输入文本的长度和输出符号的长度都是可变的, 互信息作为损失函数的一部分以获得更高的数据率。
此外, 输入文本的长度和输出符号的长度都是可变的, 互信息作为损失函数的一部分以获得更高的数据率。
而且, 提出一种句子相似度指标用以评价语义误差, 它和人类判断接近。
DeepSC 特别在低信噪比的系统中表现更好。
所提的迁移学习加持的DeepSC能够适应不同的信道以及有快速收敛的知识。
总结语义通信系统和传统通信系统的不同:
- 不同的数据处理域。 语义通信在语义域, 而传统通信在熵域压缩数据。
- 不同的通信目标。 传统通信系统专注于准确地恢复数据, 而语义通信系统为决策或者通信的目标服务。
- 不同的设计。 传统通信系统设计并优化信息传输模块, 它包含传统的transceiver, 而语义通信系统从源信息到应用目标联合设计整个数据信息处理过程。