快速排序——分治
快速排序
1、 确定分界点 $q[l]$, $q[(l + r) / 2]$, $q[r]$ 随机 2、 调整区间: 使得左边的数小于等于 $x$, 右边的数大于等于 $x$。 3、 递归处理左、右两段。
代码模板:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def quick_sort(arr, left, right):
if left >= right: return
i = left - 1
j = right + 1
x = arr[(i + j) // 2]
while left < right:
while True:
i += 1
if arr[i] >= x: break
while True:
j -= 1
if arr[j] <= x: break
if i < j:
arr[i], arr[j] = arr[j], arr[i]
else:
break
quick_sort(arr, left, j)
quick_sort(arr, j + 1, right)
n = int(input())
a = list(map(int, input().split()))
quick_sort(a, 0, n-1)
print(' '.join(map(str, a)))
快速选择算法
- 找到分界点 $x$, $q[L], q[(L + R) / 2], q[R]$
- 左边所有数 $Left <= x$, 右边所有数 $Right >= x$
- 递归排序 Left, 递归排序 Right
归并排序——分治
归并排序
- 确定分界点 $\text{mid} = (l + r) / 2$
- 递归排序 left, right
- 归并——合二为一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def merge_sort(arr, l, r, tmp):
if l >= r: return
mid = (l + r) // 2
merge_sort(arr, l, mid, tmp)
merge_sort(arr, mid + 1, r, tmp)
i = l
j = mid + 1
k = 0
while (i <= mid and j <= r):
if arr[i] <= arr[j]:
tmp[k] = arr[i]
i += 1
else:
tmp[k] = arr[j]
j += 1
k += 1
while i <= mid:
tmp[k] = arr[i]
i += 1
k += 1
while j <= r:
tmp[k] = arr[j]
j += 1
k += 1
i, j = l, 0
while i <= r:
arr[i] = tmp[j]
i += 1
j += 1
n = int(input())
arr = list(map(int, input().split()))
tmp = [0] * n
merge_sort(arr, 0, n - 1, tmp)
print(' '.join(map(str, arr)))
逆序对的数量
归并排序:
- [L, R] => [L, mid], [mid + 1, R]
- 递归排序 [L, mid] 和 [mid + 1, R]
- 归并, 将左右两个有序序列合并成一个有序序列

- 左半边内部的逆序对数量: merge_sort(L, mid)
- 右半边内部的逆序对数量: merge_sort(mid + 1, R)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def merge_sort(arr, l, r, tmp):
if l >= r: return 0
mid = (l + r) // 2
res = merge_sort(arr, l, mid, tmp) + merge_sort(arr, mid + 1, r, tmp)
k = 0
i = l
j = mid + 1
while i <= mid and j <= r:
if (arr[i] <= arr[j]):
tmp[k] = arr[i]
k += 1
i += 1
else:
res += mid - i + 1
tmp[k] = arr[j]
k += 1
j += 1
while i <= mid:
tmp[k] = arr[i]
k += 1
i += 1
while j <= r:
tmp[k] = arr[j]
k += 1
j += 1
i = l
j = 0
while i <= r:
arr[i] = tmp[j]
i += 1
j += 1
return res
n = int(input())
arr = list(map(int, input().split()))
tmp = [0] * n
print(merge_sort(arr, 0, n - 1, tmp))
二分

当找红色分界点时, $\text{mid} = \frac{l + r + 1}{2}$
\[\text{if} (\text{checkmid}) \begin{cases} true & [mid, r] : l = mid \\ fasle & [l, mid - 1] : r = mid - 1 \end{cases}\]当找绿色分界点时, $\text{mid} = \frac{l + r}{2}$
\[\text{if} (\text{checkmid}) \begin{cases} true & [1, mid] : r = mid \\ fasle & [mid + 1, r] : l = mid + 1 \end{cases}\]如何选择模板?
根据 checkmid 函数检查如何更新 mid
如果是 $l = mid$, 那么就要补上 +1
如果是 $r = mid$, 那么就不用补上 +1
为什么要补上 +1 ?
因为 C++ 默认是下取整, 当 $l = r -1$ 时, 那么 $mid = \frac{l + r}{2} = \frac{l + l + 1}{2} = l$ , $l$ 和 $r$ 没变, 陷入死循环。
数的范围
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def binary_search(arr, k):
l = 0
r = len(arr) - 1
while l < r:
mid = (l + r) // 2
if arr[mid] >= k:
r = mid
else:
l = mid + 1
if arr[l] != k:
return [-1, -1]
left = l
l = 0
r = len(arr) - 1
while l < r:
mid = (l + r + 1) // 2
if arr[mid] <= k:
l = mid
else:
r = mid - 1
return [left, l]
n, q = map(int, input().split())
arr = list(map(int, input().split()))
for i in range(q):
k = int(input())
res = binary_search(arr, k)
print(' '.join(map(str, res)))
## 数的三次方根
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def binary_search(l, r, k):
while (r - l) > 1e-8:
mid = (l + r) / 2
if mid ** 3 >= k:
r = mid
else:
l = mid
return l
l = -10000
r = 10000
k = float(input())
print(binary_search(l, r, k))
# 高精度
大整数存储
## 高精度加法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def add(A, B):
if len(A) < len(B): return add(B, A)
C = []
t = 0
for i in range(len(A)):
t += A[i]
if i < len(B):
t += B[i]
C.append(t % 10)
t //= 10
if t: C.append(t)
return C
a = str(input())
b = str(input())
A, B = [], []
for i in range(len(a)-1, -1, -1): A.append(int(a[i]))
for i in range(len(b)-1, -1, -1): B.append(int(b[i]))
C = add(A, B)
for i in range(len(C)-1, -1, -1):
print(C[i], end='')
## 高精度减法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def cmp(A, B):
if (len(A) != len(B)): return len(A) > len(B)
for i in range(len(A) - 1, -1, -1):
if A[i] != B[i]: return A[i] > B[i]
return True
def sub(A, B):
C = []
t = 0
for i in range(len(A)):
t = A[i] - t
if (i < len(B)): t -= B[i]
C.append((t + 10) % 10)
if (t < 0): t = 1
else: t = 0
while(len(C) > 1 and C[-1] == 0): C.pop()
return C
a = str(input())
b = str(input())
A, B = [], []
for i in range(len(a) - 1, -1, -1): A.append(int(a[i]))
for i in range(len(b) - 1, -1, -1): B.append(int(b[i]))
if cmp(A, B):
C = sub(A, B)
else:
C = sub(B, A)
print('-', end='')
for i in range(len(C) - 1, -1, -1):
print(C[i], end='')
## 高精度乘法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def multiply(A, b):
C = []
t = 0
i = 0
while t != 0 or i < len(A):
if i < len(A):
t += A[i] * b
i += 1
C.append(t % 10)
t //= 10
while(len(C) > 1 and C[-1] == 0): C.pop()
return C
a = str(input())
b = int(input())
A = []
for i in range(len(a)-1, -1, -1): A.append(int(a[i]))
C = multiply(A, b)
for i in range(len(C)-1, -1, -1): print(C[i], end='')
## 高精度除法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def div(A, b):
C = []
r = 0
for i in range(len(A)-1, -1, -1):
r = r * 10 + A[i]
print(r)
C.append(r // b)
r %= b
C = C[::-1]
while(len(C) > 1 and C[-1] == 0): C.pop()
return C, r
a = input()
b = int(input())
A = []
for i in range(len(a)-1, -1, -1): A.append(int(a[i]))
C, r = div(A, b)
for i in range(len(C)-1, -1, -1): print(C[i], end='')
print(r)
# 前缀与差分
## 前缀和
1
2
3
4
5
6
7
8
9
10
n, m = map(int, input().split())
arr = [0] + list(map(int, input().split()))
pre_sum = [0] * len(arr)
for i in range(1, n+1):
pre_sum[i] = pre_sum[i-1] + arr[i]
for _ in range(m):
l, r = map(int, input().split())
print(pre_sum[r] - pre_sum[l-1])
## 子矩阵的和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
n, m, q = map(int, input().split())
matrix = [[0] * (m + 1)]
for i in range(n):
arr = [0] + list(map(int, input().split()))
matrix.append(arr)
S = matrix
for i in range(1, n + 1):
for j in range(1, m + 1):
S[i][j] += S[i-1][j] + S[i][j-1] - S[i-1][j-1]
for i in range(q):
x1, y1, x2, y2 = map(int, input().split())
print(S[x2][y2] - S[x1-1][y2] - S[x2][y1-1] + S[x1 - 1][y1 - 1])
## 差分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def insert(b, l, r, c):
b[l] += c
b[r+1] -= c
n, m = map(int, input().split())
nums = [0] + list(map(int, input().split()))
queries = [tuple(map(int, input().split())) for _ in range(m)]
b = [0 for _ in range(n + 2)]
for i in range(1, n+1):
insert(b, i, i, nums[i])
for query in queries:
insert(b, *query)
res = [0] * (n+1)
for i in range(1, n+1):
res[i] = res[i-1] + b[i]
print(' '.join(map(str, res[1:])))
## 差分矩阵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def insert(b, x1, y1, x2, y2, c):
b[x1][y1] += c
b[x2+1][y1] -= c
b[x1][y2+1] -= c
b[x2+1][y2+1] += c
n, m, q = map(int, input().split())
a = [[ 0 for i in range(m+2)] for i in range(n+2)]
b = [[0 for i in range(m+2)] for i in range(n+2)]
for i in range(1, n+1):
row = list(map(int, input().split()))
for j in range(1, m + 1):
a[i][j] = row[j-1]
insert(b, i, j, i, j, a[i][j])
while q:
q -= 1
x1, y1, x2, y2, c = map(int, input().split())
insert(b, x1, y1, x2, y2, c)
for i in range(1, n+1):
for j in range(1, m+1):
b[i][j] += b[i-1][j] + b[i][j-1] - b[i-1][j-1]
print(b[i][j], end=' ')
print()
# 双指针算法
## 最长连续不重复子序列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
n = int(input())
q = list(map(int, input().split()))
s = [0] * 100010
res = 0
i = j = 0
while i < n:
s[q[i]] += 1
while j < i and s[q[i]] > 1:
s[q[j]] -= 1
j += 1
res = max(res, i - j + 1)
i += 1
print(res)
## 数组元素的目标和
1
2
3
4
5
6
7
8
9
10
11
12
13
n, m, x = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))
i = 0
j = m -1
while i< n:
while j >= 0 and A[i] + B[j] > x:
j -= 1
if j >= 0 and A[i] + B[j] == x:
print(f'{i} {j}')
break
i += 1
## 判断子序列
1
2
3
4
5
6
7
8
9
10
11
n, m = map(int, input().split())
a = list(map(int, input().split()))
b = list(map(int, input().split()))
i = j = 0
while i < n and j < m:
if a[i] == b[j]: i += 1
j += 1
if (i == n): print("Yes")
else: print("No")
# 位运算
## » k & 1
求 n 的二进制表示中第 k 位是几。
- 先把第 k 位一道最后一位 $n » k$
- 看个位是几 $x & 1$
因此方法就是: $n » k & 1$
lowbit
返回 x 的最后一位 1
\[x = 1010 \qquad lowbit(x) = 10\] \[x = 101000 \qquad lowbit(x) = 1000\]如何实现lowbit:
\[x & -x = x & (~x + 1)\] \[x = 1010 ... 10 ... 0\] \[~x = 0101 ... 01 ... 1\] \[~x + 1 = 0101 ... 10 ... 0\]1
2
3
4
5
6
7
8
9
10
n = int(input())
arr = map(int, input().split())
for x in arr:
s = 0
i = x
while i:
s += 1
i -= i & -i
print(s, end=' ')
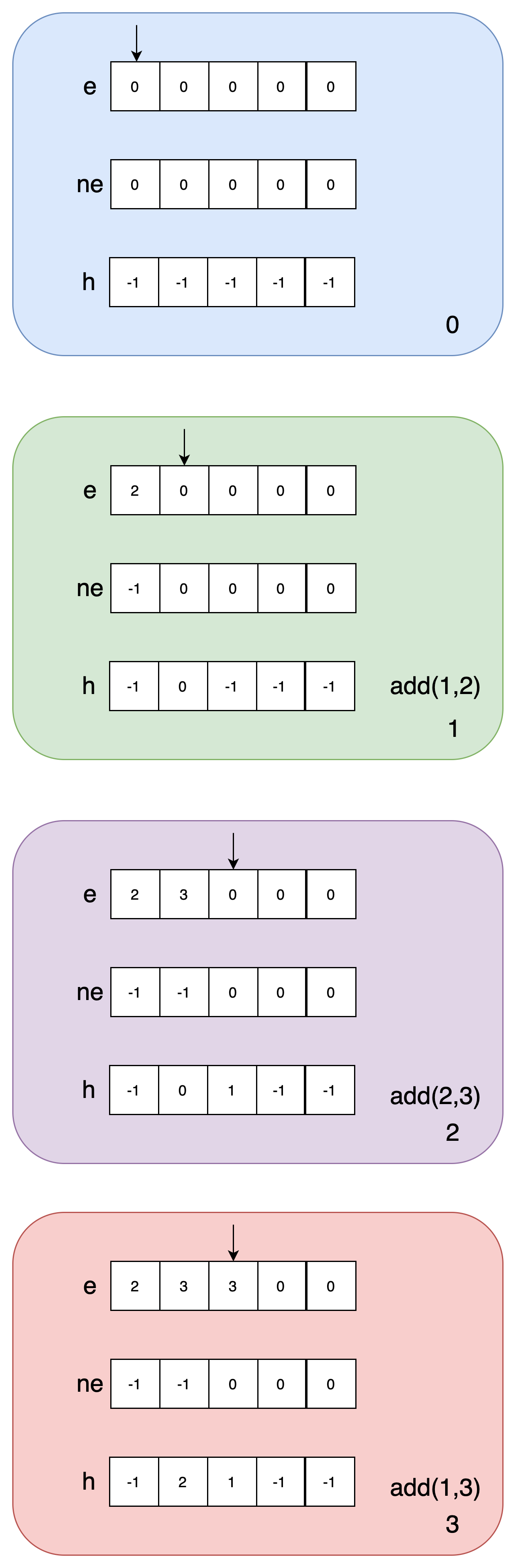
# 单链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
def add_to_head(x):
global idx, head
e[idx] = x
ne[idx] = head
head = idx
idx += 1
def add(k, x):
global idx
e[idx] = x
ne[idx] = ne[k]
ne[k] = idx
idx += 1
def remove(k):
ne[k] = ne[ne[k]]
N = 100010
n = int(input())
e = [0] * N
ne = [0] * N
idx = 0
head = -1
for i in range(n):
op = input().split()
if op[0] == 'H':
add_to_head(int(op[1]))
elif op[0] == 'I':
add(int(op[1]) - 1, int(op[2]))
else:
k = int(op[1])
if k:
remove(k - 1)
else:
head = ne[head]
i = head
res = []
while i != -1:
res.append(e[i])
i = ne[i]
print(' '.join(map(str, res)))
# 双链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# 在节点 k 的右边插入一个数 x
def insert(k, x):
global idx
e[idx] = x
l[idx] = k
r[idx] = r[i]
r[k] = idx
idx += 1
def remove(k):
l[r[k]] = l[k]
r[l[k]] = r[k]
N = 100010
e = [0] * N
l = [0] * N
r = [0] * N
idx = 2
m = int(input())
r[0] = 1
l[1] = 0
idx = 2
for i in range(m):
inp = input().split()
if inp[0] == 'L':
x = int(inp[1])
insert(0, x)
if inp[0] == 'R':
x = int(inp[1])
insert(l[1], x)
if inp[0] == 'D':
k = int(inp[1])
remove(k + 1)
if inp[0] == 'IL':
k, x = int(inp[1]), int(inp[2])
insert(l[k + 1], x)
if inp[0] == 'IR':
k, x = int(inp[1]), int(inp[2])
insert(k + 1, x)
i = r[0]
while i != 1:
print(e[i], end=' ')
i = r[i]
栈
模拟栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Stack():
def __init__(self):
self.items = []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def empty(self):
if len(self.items) == 0:
return 'YES'
else:
return 'NO'
def query(self):
return self.items[-1]
m = int(input())
S = Stack()
for i in range(m):
inp = input().split()
if inp[0] == 'push':
S.push(int(inp[1]))
if inp[0] == 'pop':
S.pop()
if inp[0] == 'empty':
print(S.empty())
if inp[0] == 'query':
print(S.query())
表达式求值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def eval():
b = num.pop()
a = num.pop()
c = op.pop()
if c == '+':
x = a + b
elif c == '-':
x = a - b
elif c == '*':
x = a * b
elif c == '/':
x = int(a / b)
num.append(x)
pr = {
'+': 1,
'-': 1,
'*': 2,
'/': 2,
}
digits = ('0', '1', '2', '3', '4', '5', '6', '7', '8', '9')
num = []
op = []
strs = input().strip()
i = 0
while i < len(strs):
c = strs[i]
if c in digits:
x = 0
j = i
while j < len(strs) and strs[j] in digits:
x = x * 10 + int(strs[j])
j += 1
i = j - 1
num.append(x)
elif c == '(': op.append(c)
elif c == ')':
while op[-1] != '(': eval()
op.pop()
else:
while (len(op) > 0 and op[-1] != '(' and pr[op[-1]] >= pr[c]):
eval()
op.append(c)
i += 1
while len(op): eval()
print(num[-1])
模拟队列
单调栈
1
2
3
4
5
6
7
8
9
10
11
12
N = 100010
stk = [0] * N
tt = 0
arr = list(map(int, input().split()))
n = int(input())
for x in arr:
while tt and stk[tt] >= x: tt -= 1
if not tt: print("-1 ")
else: print(stk[tt])
tt += 1
stk[tt] = x
邻接表