神经网络在过去的十年里取得了巨大的成功。然而，早期的神经网络只能使用 regular 数据或欧几里得数据来实现，而现实世界中的很多数据都是非欧几里得的图结构。数据结构的 non-regularity 导致了图神经网络的最新进展。在过去的几年里，各种各样的图神经网络被开发出来，图卷积网络(GCN)就是其中之一。GCNs也被认为是一种基本的图神经网络变体。

在本文中，我们将深入研究由 Thomas Kipf 和 Max Welling 开发的图卷积网络。我也将给出一些非常基本的例子，关于使用NetworkX构建我们的第一个图。在本文的最后，我希望我们能对图卷积网络的机制有更深入的了解。

Convolution in Graph Neural Networks

如果你熟悉卷积神经网络中的卷积层，那么GCNs中的卷积基本上是相同的操作。它指的是将输入神经元与一组通常称为 filter 或 kernel 的权值相乘。 filters 在整张图像上作为一个滑动窗口使得 CNN 从邻近单元学习特征。在同一层中，整个图像将使用相同的 filter，这被称为权重共享。例如，使用CNN对猫和非猫的图像进行分类，将在同一层中使用相同的 filter 来检测猫的鼻子和耳朵。

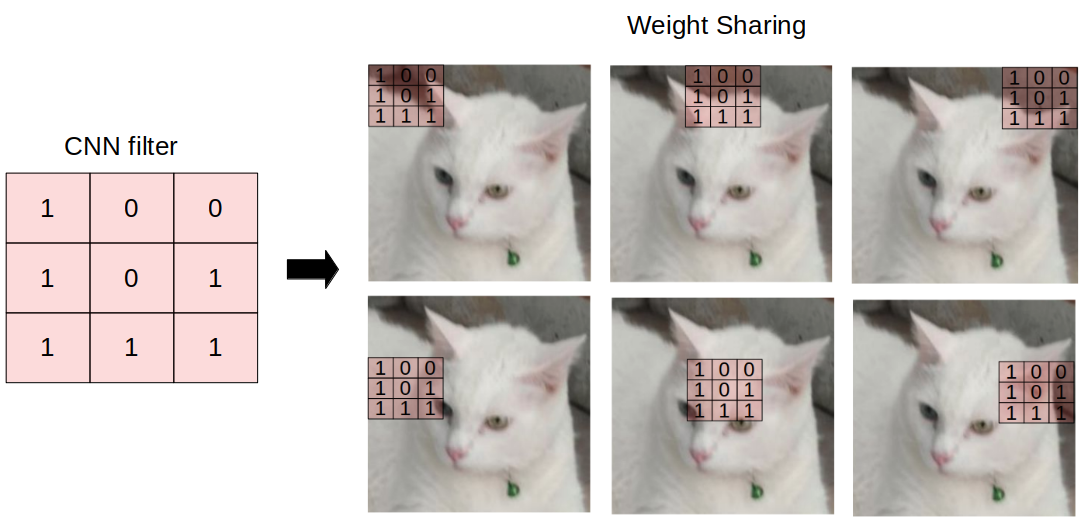
GCN 执行相似的操作，模型通过 inpect 邻近的节点学习特征。 CNN 和 GNN 的主要区别在于，CNN 是专门针对 regular (Euclidean) 结构化数据构建的，而 GNNs 是 CNNs 的广义版本，节点连接的数量是不同的，节点是无序的((irregular on non-Euclidean structured data))。

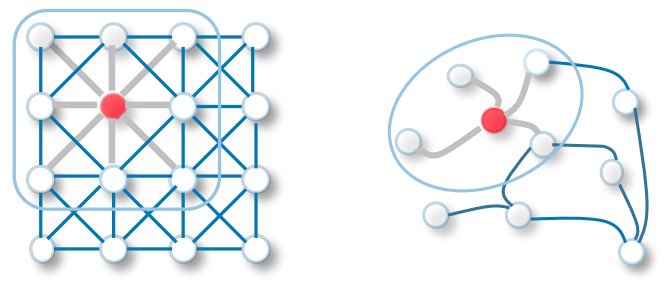
GCNs本身可以分为两种主要算法，Spatial Graph Convolutional Networks ** 和 **Spectral Graph Convolutional Networks。

Fast Approximate Spectral Graph Convolutional Networks

原始的 Spectral GCN 背后的 idea 受到 signal/wave 传播的启发。我们可以把 Spectral GCNs 中的信息传播看作是信号沿节点的传播。Spectral GCNs利用 graph Laplacian matrix 的特征分解实现了这种信息传播方法。简单地说，特征分解帮助我们理解图的结构，从而对图的节点进行分类。这有点类似于主成分分析(PCA)和线性判别分析(LDA)的基本概念，我们使用特征分解来降低维数并执行聚类。

在这种方法中，除了考虑节点特征(或所谓的输入特征)外，我们还将考虑前向传播方程中的 Adjacency Matrix(A)。A 是一个矩阵，表示前向传播方程中节点之间的边或连接。在前向传播方程中插入 A，使模型能够学习基于节点连通性的特征表示。为了简单起见，忽略偏置 b。得到的GCN可以看作是一个 message passing 网络形式的 Spectral Graph Convolution 的一阶近似，其中信息沿着图内的相邻节点传播。通过添加邻接矩阵作为一个额外的元素，前向传播方程将是：

\[H^{[i + 1]} = \sigma(W^{[i]}H^{[i]}A^*)\]

A* 是 A 的 normalized 版本。为了更好地理解为什么我们需要 normalize A，以及在 GCN 的前向传播过程中会发生什么，让我们做一个实验。

Building Graph Convolutional Networks

Initializing the Graph G

让我们从使用 NetworkX 构建一个简单的无向图(G)开始。图 G 由 6 个节点组成，每个节点的特征对应于特定的节点号。例如，节点1的节点特征为1，节点2的节点特征为2，依此类推。为了简化，我们不打算在这个实验中分配边特征。

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import fractional_matrix_power

import warnings
warnings.filterwarnings("ignore", category=UserWarning)


G = nx.Graph(name='G')

for i in range(6):
    G.add_node(i, name=i)

edges = [(0, 1), (0, 2), (1, 2), (0, 3), (3, 4), (3, 5), (4, 5)]
G.add_edges_from(edges)

print('Graph Info:\n', nx.info(G))

print('\nGraph Nodes: ', G.nodes.data())

nx.draw(G, with_labels=True, font_weight='bold')
plt.show()

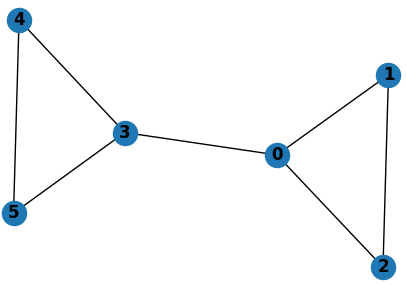
因为我们只有一个图，这个 data configuration 是 Single Mode representation 的一个例子。我们将构建一个GCN，它将学习节点的特征表示。

Inserting Adjacency Matrix (A) to Forward Pass Equation

下一步是从图 G 中获取邻接矩阵( A )和节点特征矩阵( X )。

A = np.array(nx.attr_matrix(G, node_attr='name')[0])
X = np.array(nx.attr_matrix(G, node_attr='name')[1])
X = np.expand_dims(X, axis=1)

print('Shape of A: ', A.shape)
print('\nShape of X: ', X.shape)
print('\nAdjacency Matrix (A):\n', A)
print('\nNode Features Matrix (X):\n', X)

现在，让我们研究如何通过将 A 插入到前向传播方程中来增加模型的更丰富的特征表示。我们将执行 A 和 X 的点积，在本文中，我们称这个点积运算的结果为 AX。

AX = np.dot(A, X)
print("Dot product of A and X (AX):\n", AX)

由结果可知，AX 表示相邻节点特征之和。例如，AX 的第一行对应于与节点0相连的节点特征之和，即节点1、节点2、节点3。这让我们了解了传播机制是如何在 GCNs 中发生的，以及节点连通性如何影响 GCNs 看到的隐藏特征表示。

邻接矩阵与节点特征矩阵的点积表示相邻节点特征之和。

但是，如果我们进一步思考，我们会意识到，当 AX 对相邻节点的特征进行汇总时，它没有考虑到节点本身的特征。

Inserting Self-Loops and Normalizing A

为了解决这个问题，我们现在给 A 的每个节点添加 self-loops。添加 self-loops 基本上是一种将节点连接到自身的机制。也就是说，邻接矩阵A的所有对角线元素现在都变成了1因为每个节点都与自身相连。让我们称加了自循环的 A 为 A_hat，并重新计算 AX，它现在是 A_hat 和 X 的点积：

G_self_loops = G.copy()

self_loops = []
for i in range(G.number_of_nodes()):
    self_loops.append((i, i))

G_self_loops.add_edges_from(self_loops)

print('Edges of G with self-loops:\n', G_self_loops.edges)

A_hat = np.array(nx.attr_matrix(G_self_loops, node_attr='name')[0])
print('Adjacency Matrix of added self-loops G (A_hat):\n', A_hat)

AX = np.dot(A_hat, X)
print('AX:\n', AX)

现在，你可能意识到另一个问题。AX 中的元素不是标准化的。与所有神经网络的数据预处理操作一样，我们需要 normalize 特征以避免数值不稳定以及梯度消失/爆炸。在GCNs中，我们通过计算 Degree Matrix (D) 和 inverse of D 与 AX 的点积运算来 normalize 数据

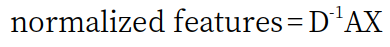
在本文中我们称之为 DAX 。在图术语中，度指的是一个节点连接到的边的数量。

Deg_Mat = G_self_loops.degree()
print('Degree Matrix of added self-loops G (D): ', Deg_Mat)

D = np.diag([deg for (n,deg) in list(Deg_Mat)])
print('Degree Matrix of added self-loops G as numpy array (D):\n', D)

D_inv = np.linalg.inv(D)
print('Inverse of D:\n', D_inv)

DAX = np.dot(D_inv,AX)
print('DAX:\n', DAX)

如果我们比较 DAX 和 AX，我们会注意到这一点

我们可以看到 normalize 对 DAX 的影响，其中对应于节点3的元素的值比节点4和节点5的值更低。但是，如果节点3的初始值与节点4、节点5相同，为什么 normalize 后的值会不同呢？

让我们回顾一下我们的图。节点3有3条关联边，而节点4和节点5只有2条关联边。节点3的度高于节点4和节点5，导致节点3的特性在DAX中的权重较低。换句话说，节点的度越低，节点属于某个组或集群的程度越高。

Kipf 和 Welling认为， symmetric normalization 会使 dynamics 更加有趣，因此，对 normalization 方程进行了修正：

让我们使用新的 symmetric normalization 方程计算标准化值：

D_half_norm = fractional_matrix_power(D, -0.5)
DADX = D_half_norm.dot(A_hat).dot(D_half_norm).dot(X)
print('DADX:\n', DADX)

回顾上一节的方程3，我们会意识到我们现在已经知道了什么是 A* !本文将 A* 称为 renormalization trick。

完成特征处理之后，是时候完成我们的GCN了。

Adding Weights and Activation Function

我们将使用 ReLu 作为激活函数构建一个2层 GCN。为了初始化权值，我们将使用随机种子，以便复现结果。只要记住权值初始化不能为0。在这个实验中，我们将设置4个神经元作为隐藏层。当我们绘制二维特征表示时，会有两个输出神经元。

为了让它更简单，我们将用numpy重写 renormalization trick 方程。

np.random.seed(77777)
n_h = 4
n_y = 2
W0 = np.random.randn(X.shape[1], n_h) * 0.01
W1 = np.random.randn(n_h, n_y) * 0.01

def relu(x):
    return np.maximum(x, 0)

def gcn(A, H, W):
    I = np.identity(A.shape[0])
    A_hat = A + I
    D = np.diag(np.sum(A_hat, axis=0))
    D_half_norm = fractional_matrix_power(D, -0.5)
    eq = D_half_norm.dot(A_hat).dot(D_half_norm).dot(H).dot(W)
    return relu(eq)

H1 = gcn(A, X, W0)
H2 = gcn(A, H1, W1)
print('Features Representation from GCN output:\n', H2)

完成了!我们刚刚建立了第一个前向GCN模型

Plotting the Features Representations

GCN 的魔力是它可以不用训练学习特征表示。让我们在通过2层GCN之后可视化特征表示。

def plot_features(H2):
    #Plot the features representation
    x = H2[:,0]
    y = H2[:,1]

    size = 1000

    plt.scatter(x,y,size)
    plt.xlim([np.min(x)*0.9, np.max(x)*1.1])
    plt.ylim([-1, 1])
    plt.xlabel('Feature Representation Dimension 0')
    plt.ylabel('Feature Representation Dimension 1')
    plt.title('Feature Representation')

    for i,row in enumerate(H2):
        str = "{}".format(i)
        plt.annotate(str, (row[0],row[1]),fontsize=18, fontweight='bold')

    plt.show()


plot_features(H2)

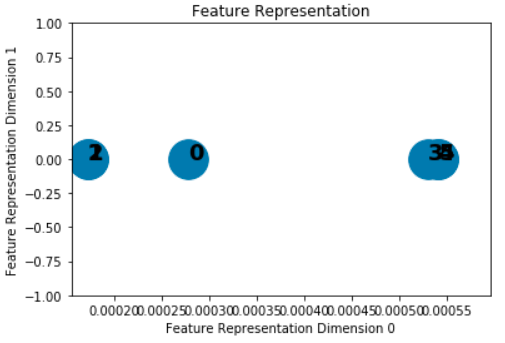
从上面的图中可以清楚地看到，主要有两组，左组包含节点0、1、2，右组包含节点3、4、5。我们可以看到 GCN 可以不用训练或反向传播学习特征表示。

Spatial Graph Convolution

不同的空间图卷积依赖于不同的 aggregators 从每个节点的邻居收集信息。从概念上讲，我们也可以将其视为 message passing。

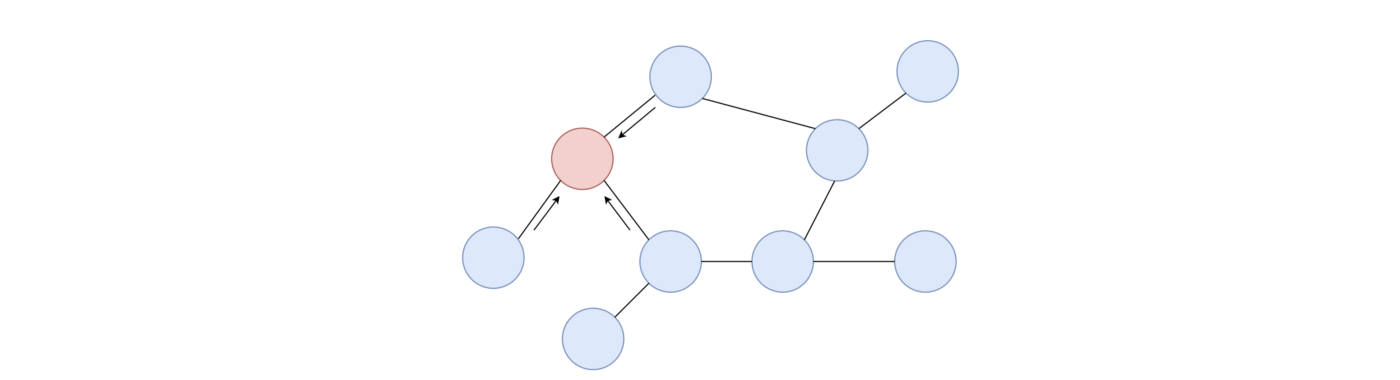
没有 Spectral 图卷积中的近似，空间图卷积通常具有更强的 scalable，因为它们的 filter 是 localized。主要的挑战是定义一个局部不变性的 CNNs, 其工作的中心节点有不同数量的邻居。在接下来的几节中，我们将快速概述不同的空间图卷积方法。我们可能会提出一些方程，有时你可能需要把这些点连起来。但为了不进一步延长文章，请参阅个别论文的细节。

Message Passing Neural Network (MPNN)

MPNN概述了空间图卷积的一般 message passing 框架。它沿着边从一个节点传递信息(message)到另一个节点，并重复k步，使信息在图中传播。下式为节点v第k层的隐藏特征表示。它取决于 v 和它在前一层的邻居的隐藏特征，以及它和邻居的边的特征。U 和 M 函数的不同选择将导致模型的不同变体。

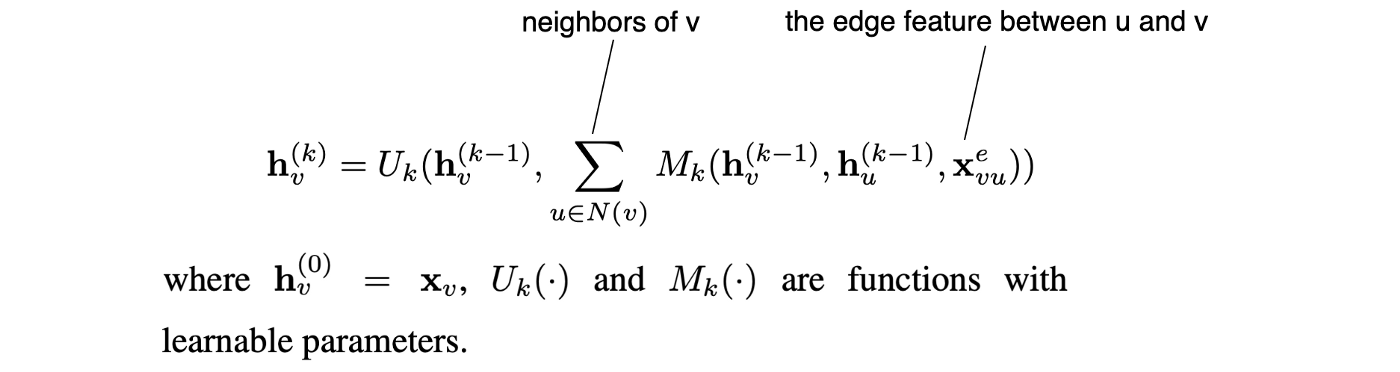
最后一个隐藏层中节点的隐表示可以传递给输出层来执行节点级预测。或者它可以传递给一个带有可学习参数的读出函数 R 来执行图级预测。

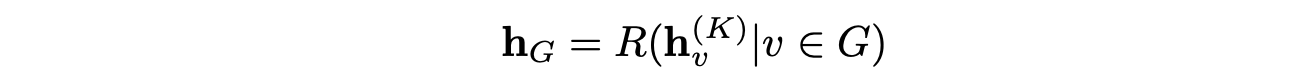
例如，在药物发现中，一个图表示以原子为节点，化学键为边的化合物。我们可能想要判别这种化合物是否能阻碍癌细胞的生长或者它是致癌的。因此，我们可以用上面的公式进行读出，进行图级预测。

Reference

Understanding Graph Convolutional Networks for Node Classification

【深度学习】Understanding Graph Convolutional Networks for Node Classification