Abstract

高光谱图像重建(HSI)的目的是在编码孔径快照光谱成像(CASSI)系统中，从二维测量数据中恢复三维空间光谱信号。

HSI表征在光谱维度上高度相似和相关。

谱间相互作用的建模有利于HSI的重建。

然而，现有的基于cnn的方法在捕获光谱相似性和长程依赖性方面存在局限性。

此外，在CASSI中，HSI信息通过编码孔径(物理掩模)调制。

然而，目前的算法并没有充分探索 Mask 对 HSI 恢复的引导作用。

这篇文章提出了一种新的框架， Mask-guided 的 Spectral-wise transformer (MST)，用于HSI重建。

具体地说，提出了一种基于光谱的多头自我注意(S-MSA)，它将每个光谱特征视为一个 token ，并沿着光谱维度计算自注意力。

此外，这篇文章定制了 Mask-guided Mechanism(MM)，引导S-MSA关注高保真光谱表示的空间区域。

大量的实验表明，MST在模拟和真实HSI数据集上显著优于最先进的(SOTA)方法，同时需要非常便宜的计算和内存成本。

Introduction

传统的基于模型的方法采用手工制作的先验，如 sparsity、total variation 和 non-local similarity 来正则化重建过程。

近年来随着深度学习的发展，深度卷积网络使用强大的模型学习端到端地从 2D measurement 到 3D HSI cube 的映射。尽管基于 CNN 的方法取得了令人印象深刻的结果，但其在内部相似度和长程依赖建模方面有限制。

此外，在CASSI中，HSI 是由 physical mask 调制的。以往基于 CNN 的方法主要采用 mask 与 shifted measurement 的内积作为输入。该方法破坏了输入的HSI信息，没有充分发挥 mask 的引导作用，改进有限。

近年来，自然语言处理中的 Transformer 模型被引入计算机视觉领域，并且在很多任务上表现超过基于 CNN 的方法。然而直接应用原始的 Transformer 于 HSI 重构是不合适的。

第一，原始的的 Transformer 学会了在空间上捕捉远程依赖关系，但 HSI 的表征在光谱上高度自相似。这种情况下，光谱间的相似性和相关性没有很好地建模。同时，光谱信息在空间上是稀疏的。捕捉空间相互作用可能不如使用相同资源建模光谱相关性划算。

第二， HSI 表征由 CASSI 系统中的 mask 调制。原始的 Transformer 在计算自注意力时，如果没有足够的引导，很容易注意到许多低保真度和信息较少的图像区域。

第三，当使用原始的全局Transformer时，计算复杂度是空间大小的二次方倍。而当使用局部基于窗口的 Transformer 时，MSA模块的感受野被限制在特定位置的窗口内，一些高度相关的 token 可能会被忽略。

这篇文章提出一种 Mask-guided Spectral-wise Transformer(MST) 用于 HSI 重构。

首先，在图2 (a)中观察到由于特定波长的限制，HSI 的每个光谱通道都捕获了同一场景的一个不完整部分。这表明HSI表征在谱维上是相似和互补的。因此，这篇文章提出了一个 Spectral-wise 的 MSA (S-MSA)来捕获长程光谱间的依赖关系。

其次，在图2 (b)中，在CASSI系统中使用一个 mask 来调制 HSI。mask 上不同位置的透光率差异较大。这表明调制后的光谱信息保真度是位置敏感的。

因此，这篇文章以 mask 为线索，提出了一种新的 mask 引导机制(mask -guided Mechanism, MM)，引导 S-MSA 模块关注具有高保真光谱表示的区域。

这篇文章的贡献总结如下：

提出了一种新的HSI重建方法，MST。可能是第一个将 Transformer 用于 HSI 重构的。
提出了一种新的 self-attention，S-MSA，以捕获HSI光谱间的相似性和依赖性。
定制了一个MM，引导S-MSA关注具有高保真 HSI 表示的区域。
MST在模拟的所有场景中都显著优于SOTA方法，同时需要更少的参数和 FLOPS。

CASSI System

一个简洁的 CASSI 系统如图2(b) 所示。给定一个 3D HSI cube，表示为 $F \in \mathbb{R}^{H \times W \times N_{\lambda}}$。 $F$ 首先被编码模板 $M^* \in \mathbb{R}^{H \times W}$ 调制为：

$F^{'}(:, :, n_\lambda) = F(:, :, n_\lambda) \odot M^*$ 其中 $F’$ 表示调制过的 HSIs, $n_\lambda \in [1, …, N_\lambda]$ 索引光谱通道， $\odot$ 表示按元素乘积。经过 disperser 后， $F’$ 变 tilted，并且沿着 y 轴 sheared。使用 $F^{‘’} \in \mathbb{R}^{H \times (W + d(N_\lambda - 1)) \times N_\lambda)}$ 表示 tilted HSI cube，其中 $d$ 表示 shifting step。假设 $\lambda_c$ 是相关波长，例如, $F^{‘’}(:, :, n_{\lambda_c})$ 没有沿着 y 轴 sheared。有：

$F^{''}(u, v, n_\lambda) = F'(x, y + d(\lambda_n - \lambda_c), n_\lambda)$ 其中 $(u, v)$ 表示系统在 detector plane 上的坐标， $\lambda_n$ 表示第 $n_\lambda -th$ 个通道，并且 $d(\lambda_n - \lambda_c)$ 表示对于在 $F’’$ 上的第 $n_\lambda-th$ 通道的空间偏移量。最后，捕获的 2D 压缩 measurement $Y \in \mathbb{R}^{H \times (W + d(N_\lambda - 1))}$ 可通过下式得到：

\[Y = \sum_{n_\lambda = 1}^{N_\lambda} F''(:, :, n_\lambda) + G\]

其中 $G \in \mathbb{R}^{H \times (W + d(N_\lambda -1))}$ 是在 measurement 上的成像噪声，由 photon sensing detector 生成。

Method

Overall Architecture

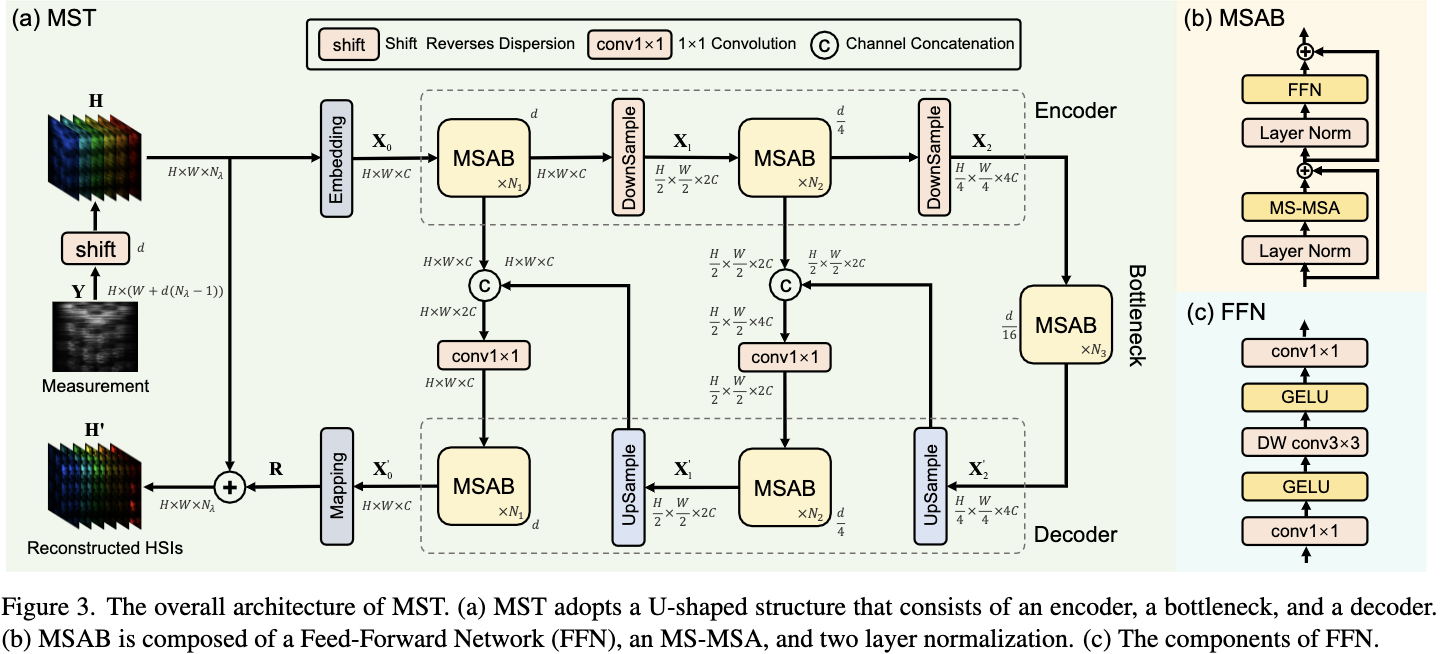
MST 的整体结构如图 3(a) 所示。采用u型结构，由一个编码器、一个 bottleneck 和一个解码器组成。MST是由 mask-guided 的 spectral-wise Attention Blocks (MSAB) 构建的。首先实现 dipersion 逆过程， shift back measurement 来得到初始化信号 $H \in \mathbb{R}^{H \times W \times N_\lambda}$:

$H(x, y , n_\lambda) = Y(x, y - d(\lambda_n - \lambda_c))$ 然后将 $H$ 送入模型。

第一, MST使用一个 conv3x3 将 $H$ 映射为特征 $X_0 \in \mathbb{R}^{H \times W \times C}$。

第二, $X_0$ 经过 $N_1$ 个 MSABs, 一个下采样模块， $N_2$ MSABs, 和一个下采样模块生成层次化特征。

下采样模块是一个 strided conv4x4 层，它向下缩放特征，并使通道数加倍。因此第 $i$ 个 stage 的编码器被表示为 $X_i \in \mathbb{R}^{\frac{H}{2^i} \times \frac{W}{2^i} \times 2^iC}$。

第三， $X_2$ 经过 bottleneck ，其由 $N_3$ 个 MSAB 组成。

随后，遵循U-Net的精神，设计了一个对称结构的解码器。特别地，上采样模块是一个strided deconv2x2 层。

利用跳跃连接进行编码器和解码器之间的特征聚合，以减轻由下采样操作造成的信息丢失。

解码器第 i 个阶段的特征为 $X_i’ \in \mathbb{R}^{H \times W \times N_\lambda}$。

经过解码器后，特征通过一个 conv3x3 层生成 residual HSIs $R \in \mathbb{R}^{H \times W \times N_\lambda}$。

最终，重构的 HSIs $H’$ 可由 $R$ 和 $H$ 求和得到。

在实现中，将 C 设为 28, 改变 (N1, N2, N3) 的组合来建立不同大小和计算量的 MST： MST-S(2, 2, 2)， MST-M(2, 4, 4) 和 MST-L(4, 7, 5)。

MST的基本单元是MSAB。如图3 (b)所示，MSAB由两层归一化组成，Mask-guided Spectral-wise MSA (MS-MSA)和前馈网络(FFN)。FFN 的设计如图3(c)所示

Spectral-wise Multi-head Self-Attention

非局部自相似性常被利用在HSI重建中，而基于CNN的方法通常不能很好地建模。由于Transformer在捕捉非局部远程依赖关系方面的有效性，以及在其他视觉任务中令人印象深刻的性能，这篇文章旨在探索Transformer在HSI重建方面的潜力。

在将transformer直接应用于HSI恢复时，存在两个主要问题。

第一个问题是，原始的 Transformer 在空间维度上对长期依赖关系进行了建模。但是HSI表示是空间稀疏和光谱相关的，如图2 (a)所示。建模 spectral-wise 关系可能比捕获空间维度的交互更有效率。因此，这篇文章提出了S-MSA，它将每个光谱特征图视为一个 token，并沿着光谱维度计算自注意力。图2(c1) 展示 MST 在 stage 0 的 S-MSA。输入 $X_{in}\in \mathbb{R}^{H \times W \times C}$ 被 reshape 为 token $X \in \mathbb{R}^{HW \times C}$。 X 被线性投影为$Q \in \mathbb{R}^{HW \times C}$, $K \in \mathbb{R}^{HW \times C}$, $V \in \mathbb{R}^{HW \times C}$。

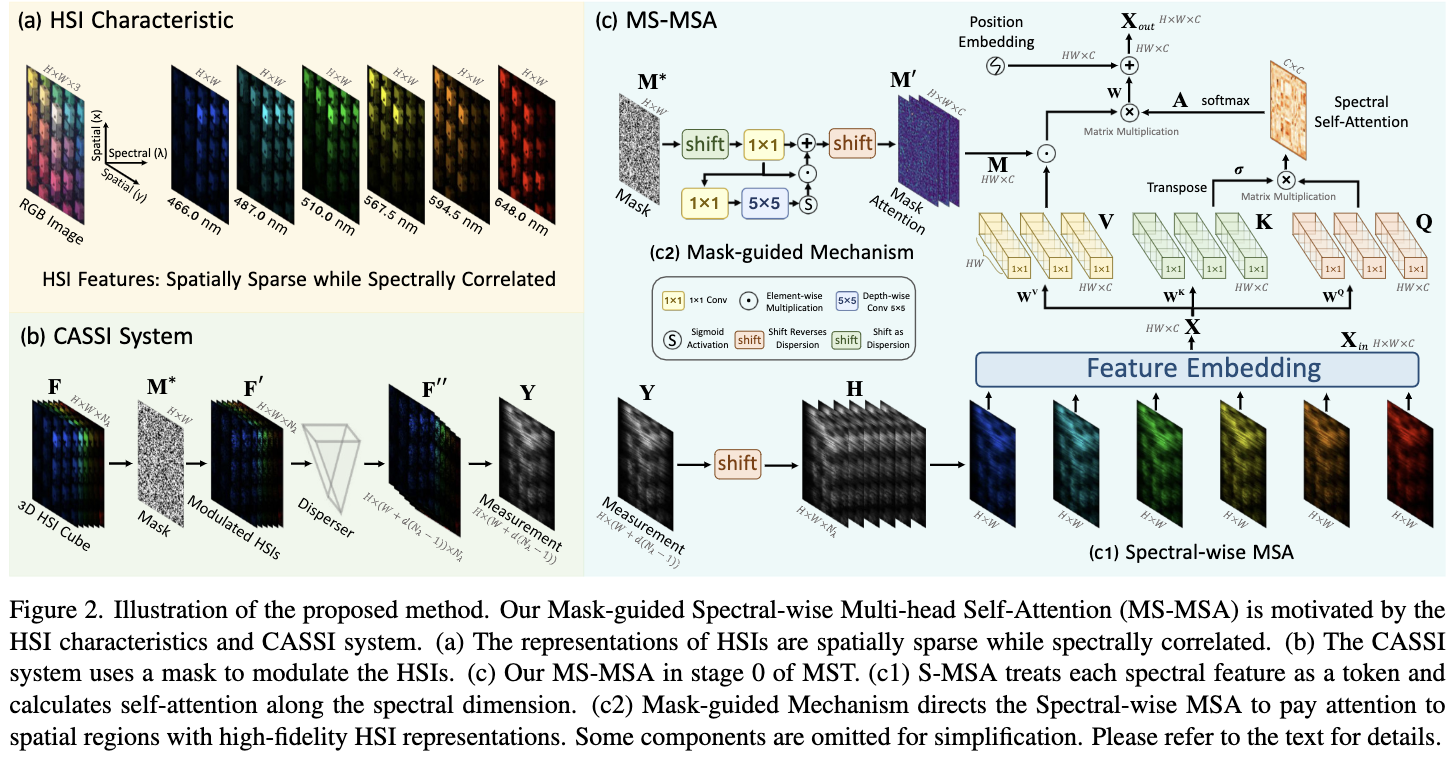图2(c1) 表示了当 N=1 的情况，一些细节为了简单省去了。与原始的MSAs不同，S-MSA将每个光谱特征视为一个 token ，并计算每个头的自注意力。

\[A_j = softmax(\sigma_j K_j^T Q_j), head_j = V_jA_j\]

由于 spectral density 随波长变化明显，使用可学习参数 $\sigma$ 通过重新加权 head 的注意力权重适应自注意力 $A_j$。然后，输出 N 个 head 在 spectral wise 拼接经过一个线性投影再和 position embedding 相加。

\[S-MSA(X) = (\mathop{Concat}_{j=1}^{N}(head_j))W + f_p(V)\]

$f_p$ 是生成 position emebdding 的函数。它由两个 depth-wise conv3x3 层，一个 GELU 激活，和 reshape 操作组成。HSI 按波长沿 spectral 维排序。因此，利用这种嵌入来编码不同光谱通道的位置信息。最后将 Eq 7 的结果 Reshape 得到特征图的输出 $X_{out} \in \mathbb{R}^{H \times W \times C}$。

Mask-guided Mechanism

直接使用 Transformer 进行HSI恢复的第二个问题是，原始 Transformer 可能会关注一些信息较少的空间区域，这些区域具有低保真 HSI 表征。在CASSI中，一个物理 mask 被用来调制 HSI。因此，mask 上不同位置的 transmittance 是不同的。因此，调制后的光谱信息具有 position-sensitive 的保真度。应该将 mask 作为指导模型关注具有高保真HSI表征的区域的线索。在这一部分中首先分析了以往基于 CNN 的方法中 mask 的使用，然后介绍了 mask -guided Mechanism (MM)。

Previous Mask Usage Scheme 以往基于 CNN 的方法主要是将初始化的 HSIs H 与 mask $M^*$ 进行内积，产生调制输入。该方案引入了空间保真度信息，但存在以下局限性:

(i)这种操作破坏了输入HSI表示，导致信息丢失，并导致空间不连续性。

(ii)这个方案只在输入时起作用。mask 在引导网络关注高保真HSI表征区域方面的引导作用尚未充分研究。

(iii)该方案没有利用可学习的参数来建模空间相关性。

MM 与以往的方法不同，MM保留了所有的输入HSI表示，并学习引导S-MSA关注高保真光谱表示的空间区域。特别地，给定如图2(c2)中的 mask $M^$, 因为调制的 HSIs 被 CASSI 系统的 disperser 偏移了，首先模拟 dispersion 过程移动 $M^$。$M^*$ 因为移动超出 y 轴的区域被设为 0。请注意，图2(c2) 显示了 MST 第 0 阶段使用的MM。为了匹配 MST 第 $i$ 阶段特征图的scale，$M_s$ 需要经过图3(a)中相同的下采样操作。 $M_s$ 经过一个 conv1x1 层，然后输入两条支路。上层支路是一种 identity mapping，以保留原始保真信息。下面的支路经过一个 conv1x1 层，一个 depth-wise conv5x5 层，一个 sigmoid 激活，和一个与上面的支路的点积。S-MSA在捕获光谱间相关性方面是有效的，但在建模HSI表示的空间相互作用方面存在局限性。因此，下面的支路被设计用来捕捉空间相关性。

为了空间上对齐 CASSI 系统(图2(b))中调制的 HSIs $F’$ 的 mask attention map 和初始化的 MST 的 $H$，逆处理 dispersion 过程，并且移动 $M_s’$ 得到 mask attention map $M’ \in \mathbb{R}^{H \times W \times C}$。

\[M'(x, y, n_\lambda) = M_s'(x, y - d(\lambda_n - \lambda_c), n_\lambda)\]

将 $M’$ reshape 为 $M \in \mathbb{R}^{HW \times C}$ 来匹配 $V$ 的维度。将 M 在 spectral wise 拆分为 N 个 heads。对于每个 head， MM 通过使用 $M_j$ 重新加权 $V_j$ 实现引导。

Experiments

Qualitative Results

Simulation HSI Reconstruction. 图4显示了使用 7 种 SOTA 方法和 MST-L，从场景5重构的仿真 HSIs 的 28 个光谱通道中选取 4 个。从重构后的HSI图(右)和所选黄框放大的 patch 可以看出，之前的方法对HSI细节的恢复效果较差。它们要么产生过于光滑的结果，牺牲了细粒度的结构内容和文本细节，要么引入了不受欢迎的 chromatic artifacts 和 blotchy textures。相比之下，MST-L更能产生感知愉悦和清晰的图像，并保留均匀区域的空间平滑性。这主要是因为 MST-L 具有调制信息的指导作用，并能捕捉到不同光谱通道的长程相关性。此外，作者绘制了光谱密度曲线(左下)，对应于RGB图像中绿色框选取的区域(左上)。曲线和真实值之间最高的相关性和一致性证明了 MST 在光谱一致性恢复方面的有效性。

Real HSI Reconstruction. 进一步将所提出的方法用于真实 HSI 重建。重新对所有 CAVE 和 KAIST 数据集的场景训练。为了模拟真实的成像情况，在训练过程中向测量中注入11 shot 噪声。视觉对比见图5。MST-L算法在高频结构细节重建和真实噪声抑制方面超过了以往的算法。

Conclusion

这篇文章提出了一种高效的基于 Transformer 的框架，MST，用于精确的HSI重建。

受HSI特性的驱动，开发了一个 S-MSA 来捕获光谱间的相似性和依赖性。

此外，定制了一个MM模块，引导S-MSA关注具有高保真HSI表征的空间区域。

利用这些新技术，建立了一系列极其高效的MST模型。

定量实验表明，该方法在很大程度上超过了SOTA算法，同时仅需要更少的参数和FLOPS。

定性比较表明，MST实现了视觉上更好的重构HSI。

【深度学习】MST：Mask-guided Spectral-wise Transformer for Efficient Hyperspectral Image Reconstruction